黄金比例与斐波纳契数列

时间：2022-03-05 理论教育版权反馈

【摘要】：斐波纳契数列的认识始于中世纪，20世纪以来不断有深入的开掘。今天，黄金比例和斐波纳契数列不仅对从事自然科学研究的学者有很大的吸引力，对从事艺术创作的画家、雕塑家、音乐家也有普遍性的影响。在数学中，“比例”用于描述类型的等同性，如9相对于3与6相对于2，这两者是相同的。我们分别由这两个问题引入黄金比例的概念。再来看一个黄金矩形，该矩形的长宽之比恰为黄金比例。

第五节　黄金比例与斐波纳契数列^[5]

黄金比例（又叫黄金分割，黄金数，φ）指的是—个不可穷尽、永不重复的数字：1.6180339887…这个数字自古代发现以来就不断触动人们的好奇心。斐波纳契数列的认识始于中世纪，20世纪以来不断有深入的开掘。今天，黄金比例和斐波纳契数列不仅对从事自然科学研究的学者有很大的吸引力，对从事艺术创作的画家、雕塑家、音乐家也有普遍性的影响。

一、“黄金比例”的提出

日常生活中，“比例”一词多用来表示事物各部分之间大小和数量的对比，或者用它来描述不同事物之间的协调关系。在数学中，“比例”用于描述类型的等同性，如9相对于3与6相对于2，这两者是相同的。

黄金比例在古代是由两个几何问题引出的。其一，是要把一条线段分成大小两段，怎样分割才合适，才符合“美”的要求——线段的黄金分割问题；其二，按照“美”的要求，一个合适的矩形其宽度与长度之比应该是多大——黄金矩形问题。我们分别由这两个问题引入黄金比例的概念。这里，毕达哥拉斯的一句名言是很有启发性的：“凡是美的东西都有共同的特性，那就是部分与部分及部分与整体之间的协调一致。”

（一）线段的黄金分割

如图1-5-1所示，一条长度为1的线段被分成两部分，使得整条线段与较长线段的比等于较长线段与较短线段的比，即，若用x表示较长部分，则，对角相乘，得1－x＝x²，即x²＋x＋1＝0，运用求根公式得：x＝

图1-5-1

因为x＞0，所以x＝

所以黄金比例

φ另一种展开式是。这是因为令a_n＝，不难证明a_n递增且有上界2，故极限存在，记对（*）取极限，得a²＝1＋a，故a＝

（二）黄金矩形、黄金三角形、正五边形与黄金比例

如果要建造一个迎面是矩形的建筑物，而且建筑物上的窗口也是矩形的，那么这两个矩形满足什么关系建筑物才协调、美观？这个问题也同样出现在美术画的画面布局、书本的封面设计中。人们经过对建筑物多年的调查研究后发现：如果一个矩形，把它切掉一个正方形后（图1-5-2），剩下的小矩形与原来的矩形相似，这个矩形及由它衍生的一系列矩形最使人赏心悦目。我们不妨将其称为“最美的矩形”。

图1-5-2

这种最美的矩形，它的宽度与长度之比也等于黄金比例φ．我们来证明这一事实。要从长度为y，宽度为x的矩形ABCD（图1-5-2）中切掉这样一个正方形CDFE．使得剩下来的矩形ABEF与原来的矩形ABCD相似，必须有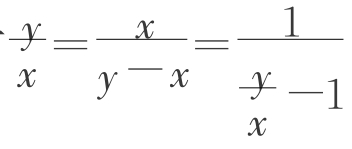，即－1＝0。

由上式可见“最美的矩形”的宽度与长度之比，应等于黄金比例φ，即＝φ

从一个“最美的矩形”中切去一个最大的正方形，剩下的小矩形仍是黄金矩形。这一过程可以无限地进行下去，从而得到无穷多个彼此相似的黄金矩形。再来看一个黄金矩形，该矩形的长宽之比恰为黄金比例。假设我们从这个矩形中切出—个正方形（图1-5-3），那么留下的较小矩形也是黄金矩形。这个“子”矩形的尺寸正好是“母”矩形的1/φ倍。若无限地重复这个步骤，我们会得出愈来愈小的矩形，看一下递减的矩形，会发现它们看起来完全相同。黄金矩形是唯一具有这种特性的矩形，即每切出一个正方形，就会产生另一个相似矩形。把任何一对母子矩形画上两条对角线，如图1-5-3所示，它们永远都会在同一点相交。这个母子系列继续在愈来愈小的矩形中延续下去，而收敛到一个永远到不了的点去。因而有西方数学家建议，把这一点称为“上帝之眼”。

图1-5-3

不仅是矩形，还有许多几何图形中隐藏着黄金比例，其中重要的例子是五角星形和黄金三角形。由一个正五边形开始，画它的对角线，便会产生一个五角星。在五角星中存在着许多黄金三角形。这些黄金三角形是等腰三角形，顶角为36°，每个底角为72°，它的腰长与它的底边长成黄金比例（图1-5-4）。

2007年10月26日澳门发行了“科学与技术—黄金比例”的一套邮票，它包含一枚小型张和四枚邮票，图1-5-5（a）是一枚小型张，图1-5-5（b）是四枚邮票中的一枚。

图1-5-4　正五边形、五角星形与黄金三角形

图1-5-5

（三）数学课堂中学生对“黄金比例”的新探究

学生在具体数学课堂教学中对前面的结论≈1.618，即“黄金比例”感到非常好奇，于是提出下面的问题：

那么

学生通过计算机求出了他们的近似值（为书写方便，分别把上述值记为R（1），R（2），R（3），…），结果见表1-5-1。

表1-5-1

从计算结果学生又提出疑问：

①为什么有些R（n）是整数？n满足什么条件时，R（n）是整数？

②R（1）＝，会不会R（2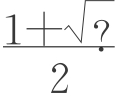）＝，R（3）＝，…，能否构造出R（n）＝

学生很容易地算出了R（2）中的“？”为9，R（6）中的“？”为25，同时又利用计算机算出了其余R（n）中的“？”，结果见表1-5-2。

表1-5-2

表1-5-2给出了上述问题的研究结果，从R（1）到R（n）的一般模式是存在的R（n）＝。但是，新的问题又出现了：这是一个代数问题，如何用代数的知识来探究为什么R（n）＝成立呢？

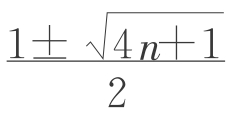学生利用已有的代数知识解决了上述问题：令R（n）＝k，即＝k，两边平方得：n＋＝k²，即k²－k－n＝0，利用求根公式得：k＝，因为k为正数，所以k＝

这样，一开始的疑问就全部解决了，而且得到了关于R（n）的两个结论：

①当n＝1时，R（1）即为黄金比例；

②要使得R（n）为整数，只需4n＋1为平方数。

但有学生又提出了另一个方向的探究性问题：P（1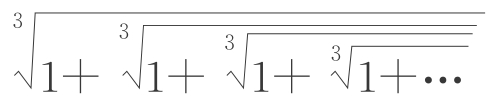）＝＝？根据极限理论得出：P³（1）＝1＋P（1），由一元三次方程求根分式得：P（1）＝（课后给出详细解法）。又有一位学生提出：是否可将三次方根推广到四次方根，即Q（1）＝＝？鉴于该问题涉及复杂的四次方程求解问题，暂时没有让学生继续探究。但进一步可引导学生探究：既然R（1）对应着一个“黄金矩形”和“黄金线段”，那么R（2）到R（n）是否也分别对应着一个“黄金矩形”和“黄金线段”呢？

二、斐波那契数列

中世纪意大利著名数学家斐波那契《算经》（又名《算盘书》）一书中有这样一道数学题：“如果每对兔子每月可生一对小兔，每对小兔在第二个月也可以生产一对小兔，如此继续下去，且不发生死亡，问一年中共可生兔多少对？”以此引出斐波那契级数列：

1，1，2，3，5，8，13，21，34，55，…

这个数列的递归公式（数学家发现的最早的递归公式之一）

图1-5-6

F₁＝F₂＝1，F_n＝F_n－1＋F_n－2（n≥3）

有意思的是，这个整数数列的通项竟然为含有无理数的一个式子，即

例5　用斐波那契数列计算规则连接的电阻、电容网络的等效值。

图1-5-7给出了一种由等值电阻R构成的电阻网络，我们想计算网络端点A、B之间的等效电阻R_等效。当网眼数n＝1，2，3，…时，网络两端相应的等效电阻为

n＝1，R等效＝2R

n＝2，R等效＝R＋

n＝3，R等效＝R＋

n＝4，R等效＝R＋

就是说，当网眼数为n＝1，2，3，4，…的电阻网络，A、B两点间的等效电阻与网络中的电阻之比分别为

图1-5-7　电阻网络

这数列与斐波那契数列中，数列完全相同，由此可知，只要知道图1-5-7中网眼的个数，就可以由数列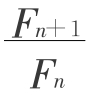求出当网眼数为n时，A、B两点间的等效电阻与网络中的电阻之比。

不难觉察到这一问题和小兔繁殖是完全相似的。可以指出，只要网眼数足够多，即n足够大，就可由数列后一项与前一项之比趋于1.618计算等效电阻的数值与网络中的已给电阻之比。

对于电阻多边形也可仿此计算。此外，注意到电容串、并联电路的等效电容公式与电阻并、串联电路的等效电阻计算公式相似，也可用相应斐波那契数列计算。

三、黄金比例与斐波那契数列的关联

令人惊奇的是斐波那契数列与黄金比例有着十分密切的关联。

我们来看看斐波那契数列前几对相继数的比：

如果我们的工作遍及整个数列，将会得到一个奇妙的性质：这一比值将明显地趋于一个极限值，该值位于1. 6180与1.6181之间，它恰好是“黄金比例”的近似值。它还能准确地以表示出来，即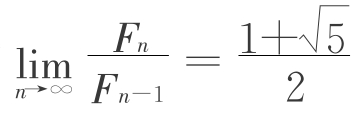＝φ≈1．618。

图1-5-8

φ比率组成的φ数列可以表示为：1，φ，φ²，φ³，…，φⁿ，φ^n＋1，φ^n＋2，…。因此，φⁿ＝φ^n－1＋φ^n－2。斐波那契数列也有类似这样的递推关系：

F_n＝F_n－1＋F_n－2（n＞2）

这是基尔拉德（A．Girard，1595—1632）1634年提出。这样，斐波那契数列、φ数列就可以用二项式系数扩展。如

F₁₀＝1F₉＋1F₈

　＝1F8＋2F7＋1F6

　＝1F7＋3F6＋3F5＋1F4

　＝1F6＋4F5＋6F4＋4F3＋1F2

这样，斐波那契数列、牛顿二项展开式与帕斯卡三角形（帕斯卡并不是这种算术三角形的创始者，图1-5-8所示利比里亚邮票上的算术三角形在帕斯卡诞生前302年，约公元1303年就出现在中国数学家朱世杰的《四元玉鉴》上，它被命名为“古法七乘方图”，图中的二项式系数一直排列到八次幂。在中国这一三角形常常称为“杨辉三角”，事实上应称为“贾宪三角”。但应该承认帕斯卡发现并证明了算术三角形的一些新的性质）。这些表面上看来毫不相关的数学内容，实质上有着深刻的联系。图1-5-10说明了它们之间的这种亲密关系：沿着帕斯卡三角形斜向点划线的数累加，便产生斐波那契数列；帕斯卡三角形的每一行，则代表二项式a＋b某个特定方展开式的系数。例如：

（a＋b）⁰＝1

（a＋b）¹＝1a＋1b

（a＋b）²＝1a²＋2ab＋1b²（a＋b）³＝1a³＋3a²b＋3ab²＋1b³

图1-5-9

图1-5-10

同样，φ¹⁰＝1φ⁹＋1φ⁸

＝1φ⁸＋2φ⁷＋1φ⁶

＝1φ⁷＋3φ⁶＋3φ⁵＋1φ⁴

＝1φ⁶＋4φ⁵＋6φ⁴＋4φ³＋1φ²

＝1φ⁵＋5φ⁴＋10φ³＋10φ²＋5φ¹＋1φ⁰

如此等等，以至无限。

φ的某些项的数值和以各种形式出现的斐波那契数列还有如下的关联：

进一步有研究表明，斐波纳契数列与中国古代由洛书演化的“九宫图”也有内在的联系。当用斐波纳契数列3，5，8，13，21，34，55，89，144依次替换三阶幻方中的数1，2，3，4，5，6，7，8，9时，会形成一个新的方阵。这一方阵虽然不具有幻方通常的性质，但它3个行的乘积的和（9078＋9240＋9360＝27678）等于三个列的乘积的和（9256＋9072＋9350＝27678）。（图1-5-11）