利用数学知识设计案例解决地球运动难点问题的尝试

利用数学知识设计案例解决地球运动难点问题的尝试

杨　萍

案例教学法是新课程所积极倡导的一种非常有效、新颖的学习方法。它一改传统课程只注重基本原理教学而不注重联系实际的做法，通过学生熟悉的一些实例，借助学生已有的知识和经验来学习,不仅能简化学习内容中的难点，而且能够使学生始终在积极兴奋的状态中获得知识，达到事半功倍的效果。

高中地理必修一“行星地球”是中学地理教学的难点，简单了，学生不知所云，复杂了，学生又不能理解，甚至有些学生直到高三毕业，还没有搞清如“正午太阳高度的计算”、“自转、公转角速度及线速度的变化规律”等问题。在教学实践中，我归纳出了利用数学、物理学科知识解决地理学科难点问题的相关案例，收到了良好的学习效果，现举例分析如下。

案例1：正午太阳高度的计算

虽然新课程对此知识点进行了简化,但其联系实际的运用仍比较普遍,如太阳能热水器的安装、房地产开发中的采光问题（楼间距的确定）等都要用到正午太阳高度的计算。此难点主要是学生对计算公式不能理解，不理解的东西也就不能用得得心应手，所以要解决这个难题，首先要让学生完全理解计算公式，进而熟练运用它。所以采用数学案例进行分析，利用了学生已有知识，易学易会。

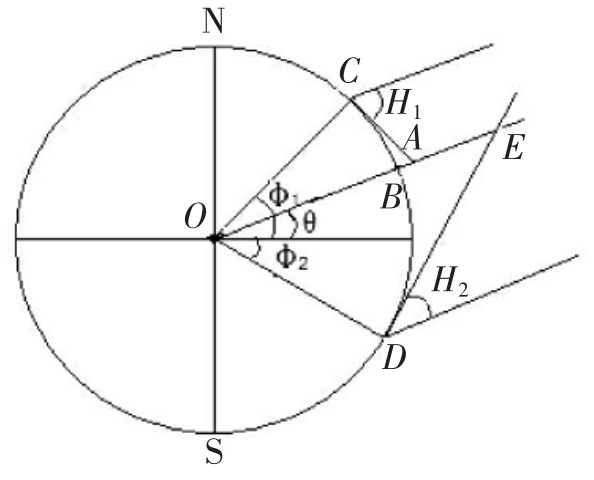
图1-1

如图1-1所示，太阳直射点（B点）的地理纬度为θ，设C点（与B点在同一个半球）的正午太阳高度为H₁，（C点纬度为φ₁）。

∵　太阳光是一束平行光　　∴H₁=∠OAC

根据正午太阳高度的定义可知：△ACO是直角三角形

∴　H₁=∠OAC=90°-（φ₁-θ）（φ₁-θ即为C点到B点的角距离）

设D点（与B点不在同一个半球）的正午太阳高度为H₂，（D点纬度为φ₂）。

∵　太阳光是一束平行光　　∴H₂=∠OED

根据正午太阳高度的定义可知：ΔEDO是直角三角形

∴　H₂=∠OED=90°-（φ₂+θ）（φ₂+θ即为D点到B点的角距离）

由上面两种情况分析可知，正午太阳高度的计算公式为：

H=90°-（计算点到直射点的角距离）

或者也可以写为：H=90°-（φ±θ）

说明：φ为计算点的地理纬度，θ为直射点的地理纬度，φ与θ在同一个半球时，取“－”号，φ与θ不在同一个半球时，取“＋”号。

利用简单的平面几何知识，通过上述案例分析，学生学得兴趣盎然，思维活跃，印象深刻，真正理解了正午太阳高度的含义,计算起来得心应手，难点也就不再是难点。

案例2：直射纬度与极昼、极夜纬度之间的关系

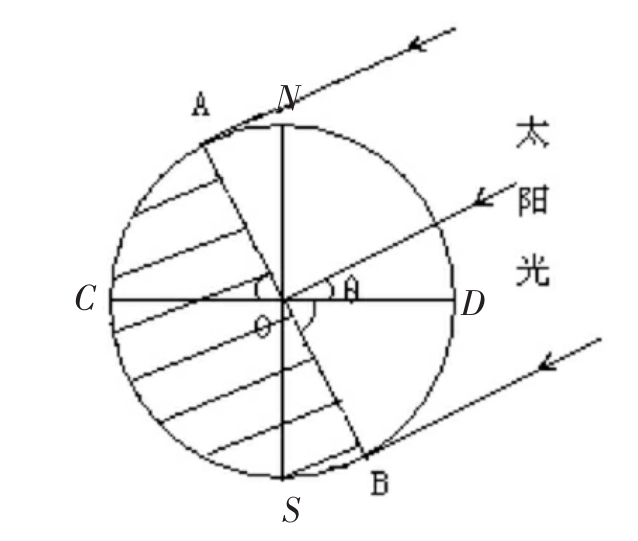
如上图所示：设太阳直射点的纬度为θ，太阳光线与北半球的切点为A，与南半球的切点为B，即AB为晨昏线。

∵　晨昏线始终与太阳光线垂直

∴　∠AON＝90°-（90°-θ）＝θ

∴　∠AOC=∠BOD=90°-θ

∴　直射点的纬度与同半球出现极昼的纬度是互余的关系，或直射点的纬度与不同半球出现极夜的纬度是互余的关系。

并由此得出：晨昏线与地轴的夹角等于直射点的地理纬度数。

掌握了这些规律，学生就能根据太阳直射的纬度，很容易判断出不同时间极昼、极夜出现的纬度范围及不同纬度极昼、极夜持续时间的长短。或者根据晨昏线与地轴的夹角判断太阳直射的纬度,从而解决相关问题。

案例3：线速度的计算

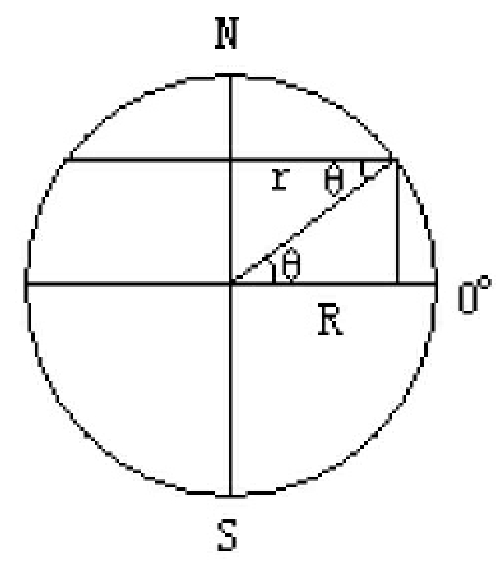
如右图所示：设赤道半径为R，地理纬度为θ处的纬线圈的半径为r

则：地球自转在赤道上的线速度：V₀=2πR/T（T为地球的自转周期）

根据圆周运动可知：纬度为θ处的地球自转线速度：

V_θ=2πr/T

∵　r=R·cosθ　　∴V_θ=2πr/T=2πR·cosθ/T=

V₀·cosθ

即：任何纬度上地球自转的线速度，等于赤道上地球自转线速度与该地地理纬度余弦值的积。

有上述原理，引导学生自主探究得出如下结论：

当θ=90°时，cosθ=0，也就是说：南北两个极点没有线速度（或线速度为0）。

当θ=60°时，cosθ=1/2，也就是说：南北纬60°处地球自转的线速度是赤道处线速度的一半。

当θ从0°到90°时，cos0°＝1，cos90°＝0，其余弦值是递减的，所以地球自转的线速度从赤道向两极递减。

案例4：公转速度在近日点和远日点时快慢的计算

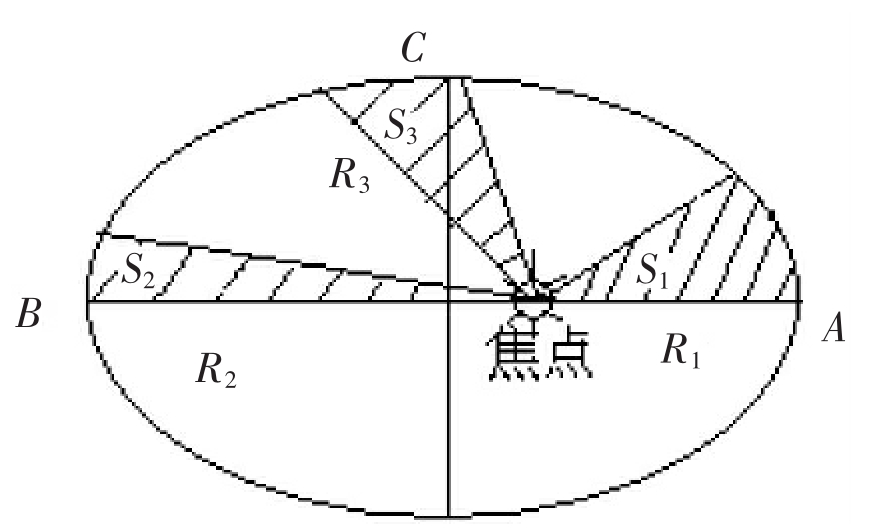
如上图所示：设近日点为A，远日点为B。

介于两点之间有C点，根据开普勒第一、第二定律：行星的公转轨道为椭圆，太阳在椭圆的一个焦点上。行星与太阳的连线在单位时间内扫过的扇形面积相等。

因为有：MVR=恒量（M——行星质量，V——线速度，R——向径）。

设地球运行至近日点A时，线速度为V1，向径（近日距）为R₁，地球运行至C点时，线速度为V₃，向径为R₃，运行至远日点B时，线速度为V₂，向径（远日距）为R₂。

则有：MV₁R₁=MV₂R₂=MV₃R₃。

当地球运行至近日点时，∵R₁＜R₃，∴V₁＞V₃，即近日点时公转速度加快。

当地球运行至远日点时，∵R₂＞R₃，∴V₂＜V₃，即远日点时公转速度变慢。

或者，利用扇形面积计算公式进行计算。

①利用角度数计算：

根据定律，S₁=S₂=S₃

∵S=nπR²/360　　又∵S₁=S₂=S₃

又∵R₁＜R₃　　∴n₁＞n₃，即近日点时角速度加快

　∵R₂＞R₃　　∴n₂＜n₃，即远日点时角速度减慢

②利用弧度数计算：

∵S=（1/2）·LR　　又∵S₁=S₂=S₃

∴（1/2）·L₁R₁=（1/2）·L₂R₂=（1/2）·L₃R₃

又∵R₁＜R₃＜R₂

∴L₁＞L₃＞L₂，即近日点时线速度加快，远日点时线速度减慢

结论：地球绕日公转的速度，近日点附近时加快，远日点附近时减慢。

利用简单的数学案例进行上面问题的分析，学生兴趣浓厚，课堂气氛活跃，地理中的难点、重点又容易理解和接受。学生也真正体会到了学科知识综合应用的魅力和案例教学的优势。以上只是一部分有关行星地球的相关计算案例，还有地方时的计算，正午太阳高度的实际应用（如：塑料大棚棚面倾角的计算，太阳能热水器集热管与楼顶夹角的计算，为保证前后两幢楼都有很好的采光条件，两幢楼之间距离的计算）等。利用案例法将所学知识与其他学科知识很好地结合起来进行分析，掌握起来容易，理解会更透彻。

（此文发表于《走进课堂—高中地理新课程案例与分析》（必修））