形式逻辑与辩证逻辑

第三节　形式逻辑与辩证逻辑

逻辑是研究思维及其规律的科学。

一、形式逻辑与辩证逻辑的关系

逻辑学分为形式逻辑、辩证逻辑和数理逻辑。

形式逻辑是关于抽象思维形式的结构及其规律的科学。

辩证逻辑是关于辩证思维形式、规律和方法的科学。

数理逻辑主要是用数学方法来研究形式逻辑中的演绎部分及以公理方法构造出命题演算与谓词演算系统的科学。

数理逻辑也可以说是“用数学方法研究数学中演绎思维和数学基础的科学”。数理逻辑研究的对象主要是命题运算、谓词运算、递归论，证明论、集合论和模型论等。

数理逻辑运用数学符号和方法把形式逻辑学提高到一个新的高度，促进数学的发展，开辟了数学研究的新领域——非标准分析。数理逻辑关于形式语言研究为计算机语言提供了前提，促进了计算机的发展。

1.形式逻辑与辩证逻辑的研究对象

形式逻辑是以抽象思维的逻辑形式、逻辑思维规律和逻辑思维方法为其研究对象的科学。

思维形式是思维对客观特定对象及其属性的反映方式，是揭示思维内容各部分之间的联系的方式，亦是思维内容赖以依存的形式。抽象思维的逻辑形式就是通常所指的逻辑思维形式。主要有概念、判断和推理等。

形式逻辑思维规律是指人们在思维过程中运用逻辑思维形式所必须遵守的普遍思维规律，也就是在运用概念组成判断，判断组成推理所遵守的规律。形式逻辑思维的基本规律有同一律、矛盾律和排中律，以及推理过程必须遵守的理由充足律。

同一律、矛盾律（也称不矛盾律）和排中律是保证思维活动具有确定性、一贯性和明确性，而理由充足律是保证思维的论证性。

形式逻辑思维基本规律是客现存在的普遍规律，是正确思维的必要前提，它对思维有制约性和规范性。

形式逻辑除了研究思维的逻辑形式及其基本规律之外，还研究人们在认识客观事物过程中使用的一些逻辑方法，比如：定义、划分、限制与概括，探求因果联系和论证等方法。

总之，形式逻辑是研究思维的逻辑形式及其规律和一般简单的逻辑方法的科学。

辩证逻辑的研究对象是思维发展规律、思维形式的辩证性、辩证思维的方法以及人们获取真理的一般途径。

辩证逻辑的逻辑思维形式仍是概念、判断和推理，辩证逻辑着重研究概念的内部矛盾的转化、概念的发展，并从事物内部与其形式的关系研究概念间的联系。辩证逻辑研究判断的相互矛盾与统一关系，研究推理所遵循的客观事物发展规律。

辩证逻辑研究的思维规律是辩证思维过程中所必须遵守的规律，它是对立统一规律，质量互变规律和否定之否定规律。

对立统一规律是要求思维过程坚持思维的辩证性，思维必须保持对立统一性，即对事物内部矛盾运动的认识既是对立的又是相互统一的，矛盾双方处在一个共同体之中。

质量互变规律是要求思维过程坚持思维的转变性，即坚持对事物内部矛盾互相转换的特征，和对事物的发展依赖于质与量之间变化的认识，把握量的变化积累到一定程度之后，质也随之变化，而质的变化必定影响量的变化。

否定之否定规律，是要求思维过程坚持思维发展性，即坚持思维在肯定——否定——否定——肯定的过程中发展，形成思维的良性循环。

2.形式逻辑与辩证逻辑的联系和统一

人们的思维过程存在着两种逻辑——形式逻辑与辩证逻辑，它们在客观上制约着思维活动，任何正确思维不仅要遵守形式逻辑规律，而且要遵守辩证逻辑规律，思维既是形式逻辑的研究对象，也是辩证逻辑的研究对象，恩格斯说过“…研究人类思维的规律的科学，即是逻辑和辩证法，…”辩证逻辑究其实质是辩证法，它是以思维发展规律为研究对象的。

形式逻辑和辩证逻辑都是以思维形式、思维方法、思维规律为其研究对象，但它们是从不同角度、不同侧面去反映思维的规律。它们之间有着密切的联系，形式逻辑是通过抽象思维建立起来的思维形式——概念、判断、推理，揭示思维的规律，而辩证逻辑思维是借助形式逻辑的思维形式，揭示思维形式与其内容间的联系以及思维形式与思维形式之间内部矛盾和发展。抽象思维是辩证思维产生的前提和基础。只有当思维发展到一定程度才能产生辩证思维。

辩证思维与抽象思维之间的关系，如同数学中的“高等数学”与“初等数学”之间的关系，初等数学主要是研究常量的数学，而高等数学主要是研究变量的数学，高等数学在初等数学基础上发展起来，高等数学的发展又促进初等数学的研究，为初等数学中不能彻底解决的问题作出理论的解答。同样地，形式逻辑是研究相对固定的思维形式的规律，而辩证逻辑则是研究思维形式间的联系、变化和发展。因此形式逻辑和辩证逻辑之间是相辅相成，作为统一思维的两个侧面并存于人们的思维之中。

3.形式逻辑与辩证逻辑的区别

形式逻辑与辩证逻辑的主要区别，在于用不同的观点认识思维、思维形式和思维规律。

辩证逻辑是用运动、变化和发展观点来认识思维的，而形式逻辑则是用固定、静止和孤立的观点认识思维的。形式逻辑撇开事物的具体内容，以揭示正确思维形式结构为主要任务，按照这些结构形式研究其思维方法和思维规律，在研究方法上，形式逻辑把思维形式看作相对固定的，不变的。辩证逻辑是动态逻辑。辩证逻辑研究的思维形式是生动的思维内容形式。正如列宁指出“黑格尔要求这样的逻辑，其中形式是有内容的形式，是活生生的实在的内容的形式，是和内容不可分离地联系着的形式”。

概念是最基本的思维形式，形式逻辑中的概念是反映事物本质属性的思维形式，这些概念是相对固定不变的。辩证逻辑研究的概念则是运动、变化和发展着的客观事物的本质、全体和内部联系。在辩证逻辑观点下，概念具有辩证性。概念内部有着自身的矛盾，即内涵与外延的矛盾。概念自身在不断发展。如函数概念的发展经历了几个阶段，概念并不是永恒不动的，是相互转化的。如物理学上的光的概念，由牛顿的粒子性发展到惠更斯的波动性，最后光是粒象和波动性的统一体。又如数的概念由正数发展到负数，继而正、负数统一在有理数域内。

判断是在概念基础上建立起来的思维形式。形式逻辑是从纯形式上研究判断的。把各类判断并列在同一水平上，只是机械地结合，并没有什么有机的联系。辩证逻辑所研究的判断是展开了的概念，它更充分地揭示事物的本质，全体和内部联系在辩证逻辑观点下的判断具有辩证性，判断具有内部矛盾性，辩证判断反映现实客观存在的矛盾关系。如“时间是连续的，又是不连续的”，“光是粒子又是电磁波”。在人们的认识过程中，判断在不断发展，从对现象外表的判断，发展为对本质的判断，然后再发展揭示事物本质和现象的统一判断。

推理是在概念和判断的基础上建立起来的思维形式。形式逻辑是从纯形式方面来研究推理的，由此得出各种推理规律，如三段论的推理规则是人们正确思维所遵循的思维规则，只要符合三段论的形式，推理的结论就可靠，违反三段论的形式，推理结论的可靠性就不能保证。显然这种推理是撇开了事物的具体内容而纯形式地进行研究的，这样推理形式是有固定格式的，而辩证逻辑研究的推理，不是纯形式，它不撇开事物具体内容，而对事物认识的深化去进行推理，在推理过程中也使用不同的思维规律。它是着重于事物间的对立统一，相互转化和联系的推理，因此它能较好地反映事物内部联系和转化，更深刻地认识世界，预见事物未来的发展。

在辩证逻辑观点下，推理具有辩证性，推理有自身内部矛盾，推理的实质是一个思维过程，在这个过程中，已知判断和新的判断存在矛盾关系和相互转化、依赖关系。例如三段论“大前提：任意三角形之内角和等于180°，小前提：∠A、∠B、∠C是△ABC的内角，结论：所以∠A＋∠B＋∠C＝180°。”在形式逻辑上它是固定地按照三段论的格式的一种表达。但从辩证逻辑观点下，它是推理形式与内容结合的辩证推理，则这个推理是从一般向特殊转化的过程。因此，辩证逻辑的推理是具有运动和转化的推理。

辩证逻辑是以形式与内容相结合来研究思维、思维形式和思维规律的。辩证逻辑着眼于研究概念、判断和推理的内部矛盾，并以运动、变化和发展的观点认识事物的属性与其内部联系。它揭示事物在发展过程中存在的矛盾，从而认识事物的相互转化和发展规律，因此辩证逻辑是形式逻辑发展的高级阶段。

总而言之，以不同的观点研究思维，是形式逻辑与辩证逻辑的主要区别。两者之间的区别集中表现在形式逻辑的基本规律和辩证逻辑基本规律的不同。

形式逻辑的基本规律是同一律、矛盾律和排中律，这三条规律实质是维护抽象思维的同一性。因为同一律表示为“A＝A”，即A与其自身同一；矛盾律表示为“A不是非A”，是从反面、否定方面表述自身的同一，也就是维护A与A自身的同一；排中律表示为“A或非A”，即要求A与非A有明确界限，实质上仍是维护A与其自身同一原则。所以同一律、矛盾律、排中律的实质就是抽象的同一性，它是以客观事物存在相对稳定性为根据，是人类认识世界的思维的概括，它不是事物本身的发展规律，而是思维所要遵守的规律。

辩证逻辑的基本规律是对立统一，质量互变和否定之否定等规律，这三条规律实质是要求思维保持具体同一性和对立统一性，也就是要思维以事物自身内部矛盾的运动、变化、发展的观点去把握对象，揭示事物发展规律，这些规律既是思维要遵守的规律也是事物发展所遵循的规律。

二、数学中的辩证逻辑关系

数学中的辩证内容是极其丰富的。数学中的辩证逻辑关系处处可见，数学的内部矛盾运动和对立统一是数学发展的巨大的动力。数学中的辩证逻辑关系表现是多方面的。从理论到实践，从抽象到具体，从代数到几何，从概念到运算，从有限到无限，以及从方法到技巧都充满了矛盾和相互转化。

1.数学的高度抽象性与广泛应用性的辩证统一

数学表现出高度抽象的形式，成为脱离外部世界的思维产物。数学的这种抽象只是形式上与现实相对立，而在内容深处仍与现实世界密切联系着，抽象程度越高的数学内容，它越更深刻反映着实现世界的真理，这一方面已被许多事实所证明。

例如，群论的诞生，它表面上是脱离了现实的一种纯数学抽象形式，但当由群的概念建立起来的理论应用于理论结晶学时，找出晶体所有可能的对称形式总共有230种。这种理论上的结论，经现代物理学观测和研究8000多种晶体结构，均符合数学理论的分析。从而客观地检验了群的客观真实性，这也充分证实数学的高度抽象与广泛应用性是统一的。

2.数学理论与实践的辩证统一

数学的发展遵循着实践－理论－实践的发展规律。数学理论是人们认识客观实际的主观思维产物。实践是人们认识世界和改造世界的客观活动，两者之间相互对立又相互依赖，处于统一体中。

由于数学自身矛盾运动，使它永远不会停留在一个水平上，在微积分理论完成后，数学又孕育着新的起点，非欧几何诞生和群的概念的建立，又使数学进入了现代数学历程，非欧几何的理论为物理学的飞跃预备了数学工具，物理学的相对论又为非欧几何提供了实际应用。数学的发展就是在这种循环中进行着。

当今的信息时代，无疑是以电子计算机的出现为开始。电子计算机的基础理论是数学，也就是数学的理论为时代的发展奠定了基础。电子计算机的发展迅速，不但影响数学的发展，也影响着各个领域的发展，包括生命科学都发生了质的飞跃，人们的工作方式，生活环境正在朝一个新的目标，发生根本性的变化，数学的理论与实践相结合正影响着人类的未来。

3.数学公理化方法与客观基础的辩证统一

数学公理化方法是现代数学科学技术发展中极为重要的方法，它是构建数学基础强有力的工具。数学公理化方法是数学抽象的一种有效形式，是数学自身发展的高度概括的表现，由于它是多层、多级的抽象思维产物，外表远离了客观实际，被人们错觉地认为是人们的“自由思想物”；然而，数学公理化方法从它的产生到现代数学广泛应用，都是与客观基础统一的。

数学形式公理化的初始，产生于公元前300年古希腊时期，以欧几里得的《几何原本》为其标志，它是形式逻辑学与数学相结合的典范。《几何原本》的公理化是建立在大量的客观几何经验和由客观事实形成的逻辑学的基础之上的。所以公理化方法的诞生源于客观实际。

数学公理化方法被广泛应用于整理和建立某一数学学科的逻辑方法，它常常在数学学科已有一定发展，而且积累了相当丰富的经验材料之后才成为可能，例如17世纪以来，人们积累了相当丰富的概率知识，经过数学家不断抽象概括，到20世纪初才完成概率论的公理化体系，可见某一学科的公理化是以客观实践为基础的。

现代数学的某些公理体系，虽然表现为数学上无法证明，作为人们设想的东西，但这些设想在其深处仍然有着客观基础，且被客观现实所检验。例如，非欧几何学是建立在人们设想的几何公理体系之上。但它在相对论中得到了应用，并由德国克莱因在欧几里得几何上成功地构造了数学模型，验证了非欧几何的相容性，可见通过公理化建立起来的非欧几何是客观真理的反映。

4.数学中几对重要的对立统一关系

数学是现实世界的物质与时空在人们的头脑中的反映。现实世界充满着矛盾，所以由数学抽象而成的量与形之间也充满着矛盾，正如恩格斯所指出：“不仅高等数学充满着矛盾，连初等数学也充满着矛盾”。数学中的对立、统一是多方面的。在数学概念方面有正与负，曲与直，平行与相交，已知与未知，常量与变量，有限与无限，连续与间断，连续与离散，精确与近似，精确与模糊，必然与或然。在数学运算方面有加法与减法，乘法与除法，乘方与开方，微分与积分，映射与逆映射，几何变换与逆变换，算子与逆算子等等，这些都是相互对立统一地处于数学体系中，成为数学发展的动力。

下面着重阐述中学数学中常见的几对对立统一关系。

（1）已知与未知

数学中的已知与未知是成对出现的，又是互为相对的，由未知向已知转化是数学问题解决的一个根本方法。数学的发展就是不断寻求由未知向已知转化的过程。数学中常用的待定法就是一种典型由未知向已知转化的方法。列方程解应用题的设元方法就是待定法的一种表现。现代数学中的同构、映射、变换等方法就是实现由未知转向已知的重要桥梁，分析法是数学中重要的方法，它的实质是由未知向已知寻求过渡的方法，而综合法则是由已知向未知过渡的方法。两者常交替使用，因而又叫综合－分析法。由上述可见，数学中的已知与未知的矛盾和它们的转化是数学发展的一个动因。

（2）常量与变量

常量是反映事物相对静止状态的量，而变量则是反映事物运动变化状态的量，它们之间相互对立又相互依赖，又在一定条件相互转化，它们的依赖和转化，在数学中表现为以下几个方面。

①常量与变量之间具有相对性

在研究某个问题过程中，某些量被视为常量，但从另一角度去研究时，它又被看作变量。这种同一个量在不同状态下可能为常量或可能为变量，在数学中是经常被运用的。例如在研究直线方程时，y＝kx＋b中，y，x是变量，当k，b为常量时，表示一条直线，当k为常量，b为变量时，表示平面上一族平行直线，当k为变量，b为常量时，表示一族过点（0，b）的直线，可见，常量与变量是相对的。

②变量借用常量来刻划

数学中的变量是反映客观事物的变化过程的量，要揭示这个量的本质属性，仅靠描述性的叙述是不够的，需要实现量化来刻划，这就要借助于常量来表达。例如，极限概念，它表示一个变量的某一种趋势，但如何反映变量a_n无限地接近极限A呢？人们经历了2000多年，才找到用常量来刻划这个过程。那就是存在N，当n＞N时，有｜a_n－A｜＜ε，在表达式中，N，n，A，ε都是常量，而a_n又是相对的变量。通过这种数量关系，成功地揭示了极限过程。运用常量来刻度变量是数学思想方法的一大突破，是辩证关系的重大运用。

③通过变量研究常量

在数学研究过程中，有时需要确定某个量在某一状态下的值，这个值相对地是一个常量，利用常量与变量的辩证关系，可以先设这个量为一个约束条件下的变量，然后使它达到确定的状态，进而求得问题的解答。这样的化常量为变量的研究方法在数学中是常用的。其中以求极值问题为典型。

例如，半径为R的圆，内接一个矩形，问当矩形的长与宽为何值时，其面积最大。显然矩形面积达到最大值是一个常量，为求这个常量，可先化为变量研究。

（3）曲与直

曲与直是两种不同的图形，在几何图形中曲与直的区别是极其明显的。直线的曲率为0，曲线的曲率不为0，但在研究曲线与直线问题时，曲与直是相互转化的，通常由于直线和直线形的性质易于掌握，因此，化曲为直成为数学研究的一种思想方法。这种方法在数学中的例子很多，其中古代计算圆周率的方法是一个很好的范例。

（4）有限与无限

在人类认识现实世界过程中，最先接触的是有限的物质和时空，然后逐步接触和认识无限的时空。经过数学思维的加工，构成数学中的有限量与无限量。有限量与无限量在本质上是有很大区别的。有限量的许多性质对于无限量是不适用的。如有限个量之和，一个公式可交换和结合，但对于无限多个量之和不一定能交换和结合。如a₁＋a₂＋…＋a_n可交换和结合，但对于无限多个量之和不一定能交换和结合。如：

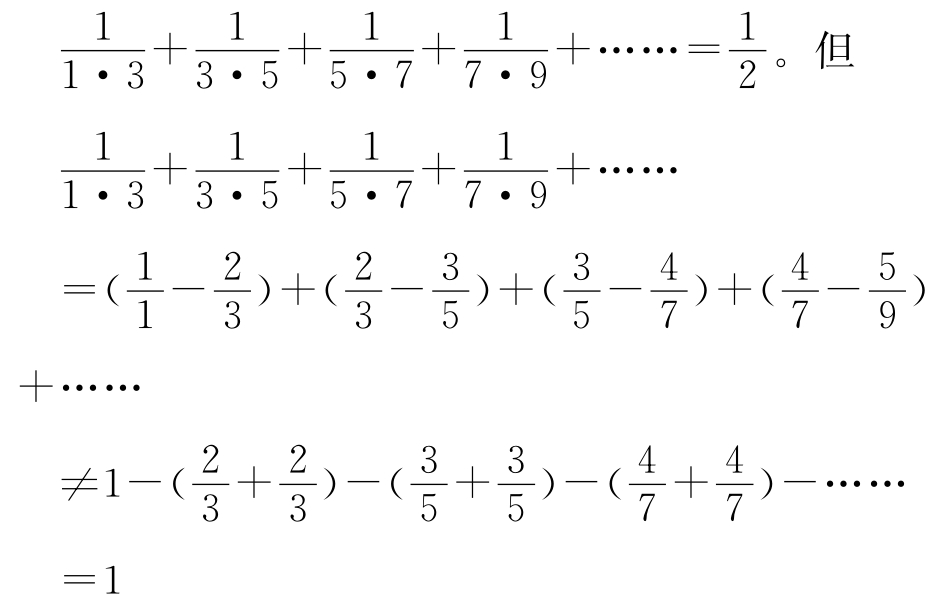
又如：作为无限集的自然数集｛1，2，3，…｝与它的子集奇数集｛1，3，5…｝是对等的，其基数相同，但有限集与其真子集是不对等的。

虽然无限与有限在本质上有差异，但它们在数学体系中是对立统一的，它们相互依赖，在一定条件下互相转化。例如用有限量去逼近无限量是数学中常用的思想方法，这在变量与常量的关系中已叙述了。用有限量来刻划无限量在平面几何中的一个例子就是两直线平行的判定定理。两直线被第三条直线所截，同位角相等，则两直线平行。

用无限量来表示有限量也是数学研究的一种基本方法，其中以函数在某一点用级数展开为最典型。

（5）连续与不连续

数学中描述的量有两类，一类是描述静止状态的量，另一类是描述运动变化的量，它们反映着两种不同的情况：连续与不连续，虽然连续与不连续在本质上是有很大差异的，但在一定条件下相互转化。

人类在认识了离散的自然数、整数之后。逐步认识有理数。虽然有理数不再是离散的，但还不是连续的。只有当揭示实数的本质属性之后，才认识到实数具有连续性，才真正理解实数与数轴上的点一一对应，数轴上的实数点之间没有任何间隙（天衣无缝）、实数的这种完备性是由三位数学家维尔斯特拉斯，戴特金。康托分别用不方式完成。其中以戴特金分割为最形象直观。他将一切有理数分为两类：A与B，其中B中任一元素都大于A中任一元素。这样的划分只能出现3种情况，（1）A中有最大元；（2）B中有最小元；（3）A中无最大元，B中无最小元，于是（1）和（2）确定一个有理数，而（3）就确定一个无理数。由这样分割可知实数是连续的，中间没有任何间隙。实数的连续性的另一表达形式就是任何一个无穷递缩闭区间套序列确定唯一的一个实数。这是从无穷变量方面去刻划实数的方式。

数学中的连续与不连续，除了在数的性质反映外，还有在函数、方程、曲线等方面的反映。在数学分析中，在研究函数性质上，可以看到连续与间断、连续与离散之间在一定条件下相互转化，例如：若函数f（x）在区间［a，b］中除点x＝c，c∈［a，a］外均连续，而f（x）在点x＝c的左、右极限存在且等于P，那么取f（c）＝p，则f（x）在区间的［a，b］为连续函数。间断点x＝c，转化为连续点。这是化间断为连续的一种常用方法。类似于这样的处理方法还有很多。

以上仅对数学中常见的对立统一关系作简要的叙述。此外还有不少的对立统一关系。如必然与或然，精确与模糊等。

5.数学方法的辩证统一

数学中的辩证关系，除了它自身的数学内容充满矛盾统一之外，还表现在数学方法、数学思想方法的辩证统一。例如，归纳法与演绎法，分析法与综合法、直接证法与间接证法等等，都是既对立又统一的数学思想方法。在数学思想方法运用上常使对立方法溶于统一过程之中。如先用归纳法探索再用演绎法证明探索的结论；用分析法与综合法结合而成的中途点法。在数学方法上，微分与积分是既对立又统一的两个数学方法，它们相互联系又相互转化，像这样的例子，数学上处处皆是。正是由于这些方法的交错运用和转化，形成了今天这样充满活力，应用极广的科学数学。

6.数与形的分离和结合的辩证统一

数与形是数学的两个主要研究对象，在数学萌芽时期和常量时期的一段漫长历史时期，数与形是被分离成两个不同的研究对象，直至在笛卡儿建立直角坐标系之后，在数与形之间架起了一座桥梁，使数与形紧密结合起来，数与形的相互转化成为可能，从此开创了数学发展的新时代。形的直观性为数学创造活动开拓了广阔的空间，数的理论推导为数学结论的确立给予了有力的支持。数与形的结合和相互转化，使数学如虎添翼，迅速发展。数形结合方法在中学数学应用甚广，成为中学数学解题方法的一个重要组成部分。