黄金数最难混沌

黄金数最难混沌

现在我们知道，耦合振子所涉及的两个频率之比是有理数时，也即比值可表示成整数之比时，运动是周期性的;比值为无理数，也即不能表示为整数之比时，运动是准周期的。准周期运动中有些容易被锁频到周期运动，也就是共振区，有些则不容易被锁进去，继续它的准周期运动。显然，越靠近有理数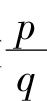的那些无理数所对应的准周期运动，越容易被锁进去;越远离有理数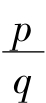的无理数所对应的准周期运动，越难以被锁进去，而坚持自己原有的运动状态。现在我们寻找坚持最久、最坚固、最不容易被锁进周期区的，也就是最难以破坏因而也是最后被破坏的准周期运动是什么样的?可以想见，这个运动所对应的那个无理数距有理数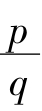最远。

由数论知识知道，一个有理数可以通过一个有限的连分数表达，一个无理数只能通过一个无限的连分数逼近;但是用无限的连分数逼近无理数时有快慢之分，其中二次无理数逼近得很慢，而黄金数逼近得最慢。

所谓连分数逼近无理数，就是一个无理数σ用如下形式的连分数近似地去代替。

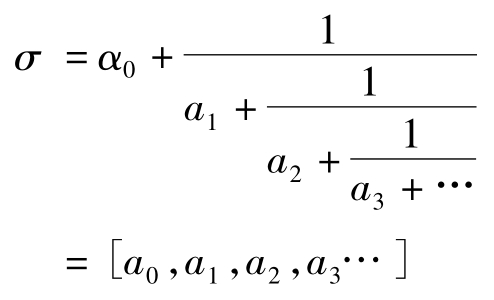
最后的括弧是连分数的简记形式，［0］表示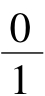，［1］表示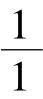，［0，1，1］表示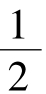，等等。所谓二次无理数是指二次方程的根为无理数，其中黄金数是二次方程

x²+ x－1=0

的正根τ=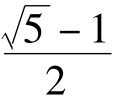=0．618

就是个二次无理数，它可以用如下的无限连分式逼近

τ=［0，1，1，1，1，…］

这是“最简单”的连分数，但比π=［3，7，15，1，292，…］，e=［2，1，2，1，1，4，1，…］这样的无理数，逼近得更慢。这就是著名的黄金分割数(简称黄金数)，来源于线段的分割。人们认为将长为L的线段按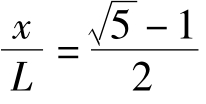的比例分割，在造型艺术上最美，如工艺美术或日用品的长宽搭配，按此比例容易引起美感。现在我们又看到，从运动稳定性上考虑，耦合振动系统的频率比为0．618…时最不容易被破坏，最不容易进入共振或锁频的重叠区，也就是说最不容易进入混沌区。一旦它也被破坏了，系统就进入全局的完全混沌状态了。0．618…是美的象征，也是稳定坚固的象征，二者是巧合还是必然?

※　※　※　※　※　※　※

寄语:

大自然在振动，社会也在振动中前进，

国家、集体和个人，大小振子协作锁频，

保持稳定共同繁荣。

识时务者顺之——昌，

不识时务逆之——亡，

客观规律不可拒抗。