二元一次不定方程

时间：2022-02-12 理论教育版权反馈

【摘要】：在对百鸡问题的介绍中，我们引出一个二元一次不定方程。即给定一个二元一次不定方程ax+by=c，先要问它否有整数解？合而言之，二元一次不定方程ax+by=c有解的充要条件是a、b的最大公约数d能够整除c。事实上，在碰到一般的二元一次不定方程时，上述方法虽然仍有效，但过程却不一定如此简单了。显然，解这一不定方程的计算量就大多了。

在对百鸡问题的介绍中，我们引出一个二元一次不定方程。对如何求解这一方程，我们没有多做介绍。在这一节中我们将探讨这一问题。

我们从一般形式的二元一次不定方程ax+by=c（a, b，c是整数，a, b不为零，x, y为未知量）求整数解着手。与古代人的研究方式不同，现代人在理论上探讨不定方程问题时，首先要探讨解的存在性问题。即给定一个二元一次不定方程ax+by=c，先要问它否有整数解？如果费力去求解一个根本没有解的不定方程就完全是白费气力了。比如，求方程3x+6y=16的整数解。有必要去具体求解吗？没有。因为容易看到，方程左边是3的倍数，而右边则不是3的倍数，因此这一方程根本不可能有整数解。显然，这样的道理可以推广到一般的二元一次不定方程ax+by=c，即：若方程左边系数a、b的最大公约数为d，那么只要d不能整除方程右边的c，则这一不定方程一定没有整数解。换言之，二元一次不定方程ax+by=c有解的必要条件是a、b的最大公约数d能够整除c。事实上，进而可以证明，a、b的最大公约数d能够整除c还是ax+by=c有解的充分条件。合而言之，二元一次不定方程ax+by=c有解的充要条件是a、b的最大公约数d能够整除c。这也意味着，在理论上探究二元一次不定方程ax+by=c整数解时，只需要考虑a、b互素（即两者的最大公约数为1）的情形即可，因为当a、b不互素时，方程两边可以同除以两者的最大公约数，以使两者的最大公约数为1。

在做了这一说明后，为了方便，我们下面讨论二元一次不定方程ax+by=c时，约定a、b互素。在这种约定下，我们研究一下它的通解。

我们先以百鸡问题中出现的二元一次不定方程7x+4y=100为例，介绍一种处理二元一次不定方程时容易理解的常用的基本方法：参数法。因为著名数学家欧拉曾在其通俗教科书《代数》（1770）一书中广泛使用这种方法，因此也称欧拉方法。

解：用x, y系数中较小的系数除方程各项，则由原方程可得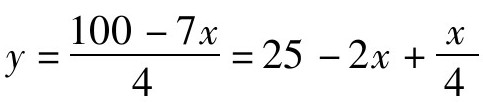，设x/4=t（t为整数），则y=25-8t+t=25-7t。

由此我们已经得到了7x+4y=100的通解。再把这一结果代入x+y+z=100，得z=75+3t。由此即得到百鸡问题的通解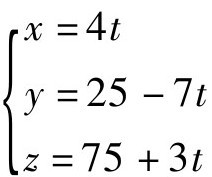：，其中t为任意整数。

看起来，这种方法很容易掌握，而且似乎计算也不复杂，但问题在于我们上面所解的方程不具有一般性。事实上，在碰到一般的二元一次不定方程时，上述方法虽然仍有效，但过程却不一定如此简单了。看下面一个例子。

求不定方程321x-111y=75的一切整数解。

解：（321，111）=3，所以方程两边可以先约去3，得到同解的不定方程107x-37y=25。

下面我们用x, y系数中较小的系数除上面方程各项，则可得：

再令t=（-1-s）/4，得s=-1-4t。把这一结果代入（2）式与（1）式，得到：

由此得到不定方程107x-37y=25的通解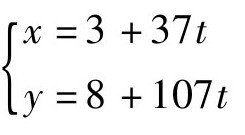：，t∈Z。

显然，解这一不定方程的计算量就大多了。能否找到更简单些的一般方法呢？为此，我们分析一下上面两个不定方程通解的构成。

7x+4y=100通解可以分成两部分：一部分（0，25）是7x+4y=100的一个特解；而另一部分（4t，-7t）恰好是齐次方程7x+4y=0的通解。而7x+4y=100这个非齐次方程最后的通解则是它的一个特解与对应的齐次方程的通解之和。同样的，321x-111y=75（或与之同解的107x-37y=25）的通解也可以分成两部分：一部分（3，8）是107x-37y=25的一个特解；而另一部分（37t，107t）恰好是齐次方程107x-37y=0的通解。而107x-37y=25这个非齐次方程最后的通解则是它的一个特解与对应的齐次方程的通解之和。

这一重要而有用的结论在数学上称为迭加原理，这一原理可以表述为：非齐次方程的通解是一个特解与对应的齐次方程的通解之和。在求解许多种类的数学方程（如高等数学中的常微分方程、差分方程等）时，都会碰到这一原理的应用。

由此结论，为求ax+by=c的通解，我们可以先求由它转化得到的齐次方程ax+by=0的通解。很显然，这个齐次方程的通解可以表示为：x=bt, y=-at, t为整数。于是若设ax+by=c的一个特解为（x0，y0），则运用这一原理可得到ax+by=c的通解：x=x0+bt, y=y0-at, t为整数。这意味着，求ax+by=c的通解的关键是求其一个特解。于是，剩下的问题是，如何才能求出ax+by=c的一个特解呢？

在某些特殊情况下，观察法就能做到。比如，通过观察可以发现（0，25）是7x+4y=100的一个特解。但我们这里寻求的是一般方法。

让我们再回到上面两个例子。分析其解法，会领悟到它们所用的方法在本质上相当于对不定方程的系数做辗转相除，依次化为等价的不定方程，直到出现一个变量系数为1或-1为止。显然，最后得到的这种形式的方程可以直接得到通解，然后再依次反推回去，就可得出原不定方程的通解。

辗转相除法是数学史上最古老的算法之一。著名数学家欧几里得将古希腊人发现的这一算法总结在其名著《几何原本》中，因此这一算法在西方称之为欧几里得算法。这一著名算法可用来求两数的最大公约数。具体来说，给出两个正整数a, b，要求它们的最大公约数（a, b）。用欧几里得算法可以如下进行：用b除a得商q1，余数r1。若余数r1不为0，则用r1除b，得商q2，余数r2……如此反复，辗转相除下去。因为每进行一次这样的步骤，余数就会减少一些，因此在经过有限步后一定会在某一步时余数为0。

用代数形式表达如下：

于是，rn=（a, b）。

举一个简单例子，求（96，54）。

由96=54×1+42；54=42×1+12；42=12×3+6；12=6×2+0。于是，（96，54）=6。

值得一提的是，中国古代求最大公约数（中算中称“等数”）的方法称作更相减损术。其方法是：从大数中减去小数，辗转相减，在经过有限步后会出现余数和减数相等，由此得到的“等数”就是现在所称的最大公约数。以上面所举题目为例，其逐步减损的步骤如下：（96，54）=（42，54）=（42，12）=（30，12）=（18，12）=（6，12）=（6，6）。于是，（96，54）=6。

两个结果是相同的。事实上，更相减损术在步骤上虽与欧几里得算法略有不同，但两者在本质上是相同的。更值得一提的是，这种方法在求多个数的最大公约数时有着非常优越之处。举一个例子。求四个数1008，1260，882，1134的最大公约数（1008，1260，882，1134）。我们可以不拘次序地挑选最方便的方式，从其中较大的数减去次大的数，一再减损，最后如能出现全部相等的余数，那么这个等数就是所求四个数的最大公约数。

具体步骤如下：（1008，1260，882，1134）=（1008-882，1260-1134，882，1134-882）=（126，126，882，252）=（126，126，882-126×6，252-126）=（126，126，126，126）=126。显然，这种算法比逐次两两求最大公约数或把四个数分解为素因数要简便得多。我国数学家张德馨（1905～1992）在所著《整数论》（1956）卷一曾介绍用这种方法求几个数的最大公约数，并在序文中说这种方法是他在德国柏林大学数学系听数论课时学来的。不了解中国古代数学的他不清楚的是，这一方法早在2000多年前就已经被中国古代数学家熟谙了。由此亦知，更相减损术在现代仍有理论意义和实用价值。

欧几里得算法（或更相减损法）除提供了求最大公约数的方法外，还有着许多其他的应用。比如，我们利用它可以找出满足ax+by=（a, b）的一组特解。

为便于理解，我们还是从特例入手，求96x+54y=6的一个特解。

方法是把用辗转相除法求（96，54）的过程反转过来：96=54×1+42；54=42×1+12；42=12×3+6；12=6×2+0。

下面，我们从倒数第二个式子开始倒推回去，于是有：6=42-12×3=42-（54-42）×3=42×4-54×3=（96-54）×4-54×3=96×4-54×7。这样，我们就得到了：6=96×4-54×7。96、54的最大公约数6已经用96、54这两个数表示出来了。这也表明，我们已经找到了96x+54y=6的一个特解：x=4，y=-7。

由此，我们可以简单说明一下有些抽象的一般结论了。

由辗转相除法倒数第二个式子可知，rn能表示成rn-1与rn-2的一次式，将结果代入倒数第三式，则rn可表示成rn-2与rn-3的一次式，将结果继续代入倒数第四式，则rn可表示成rn-3与rn-4的一次式……重复这一过程，最后rn可表示成a, b的一次式（或说可以表示为a, b的线性组合），即一定能找到两个整数s, t，使得r n=（a, b）=as+bt。也就是说，若a, b为给定的两个整数，那么它们的最大公约数一定可以通过这两个数的线性组合表示出来。

很显然，这一结果表明，通过这种方法，我们一定可以找到一次不定方程ax+by=（a, b）的一个特解。特别地，如果a, b互素，即（a, b）=1，那么ax+by=1一定有解，而且一定可以通过上面的方法找到它的一个特解。在此基础上，我们就一定可以找到ax+by=c的一个特解了。简单说，如果ax+by=1的一个特解是（x0，y0），那么我们就可以取ax+by=c的一个特解为（cx0，cy0）。

最后需要补充一点，用辗转相除法求一次不定方程的解，方程系数a, b都应为正数。如果方程ax+by=c中的系数有负数呢？很显然，因为我们所求的是整数解，因此只要得到了ax+by=c（系数全为正）的一个特解，那么我们可以马上给出ax+by=c（系数中有负数）的一个特解。比如说，我们找到了96x+54y=6的一个特解：x=4，y=-7。那么，当方程换作96x-54y=6时，我们可以直接得到其一个特解：x=4，y=7。

至此，求ax+by=c一个特解的一般方法我们已经明白了。由此，我们亦可以对ax+by=c（为方便，我们假定各系数为正）求解过程做一个总结了。首先，我们要判断这个方程是否有解，也就是说看一下c是否整除（a, b）。如果不整除，方程无解。如果整除，那么可以在原方程两边约去（a, b），于是得到与之同解的新方程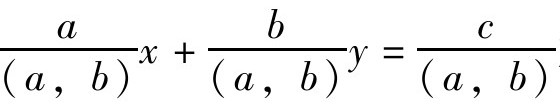左边两系数一定互质。为了求这个新方程的一个特解，我们可以利用辗转相除法先求的一个特解[设这个特解为（x0，y0）]，那么我们就可以得到新方程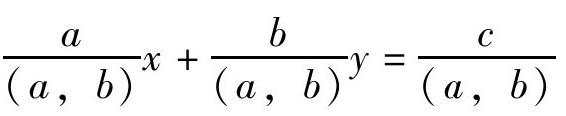的一个特解为（cx0，cy0）。最关键的特解找到了，那么我们就可以得到原方程的通解公式了。

为说明求解过程。下面，我们重新求一下上面的两个不定方程。

求7x+4y=100的一切整数解。

解：（7，4）=1｜100，方程有解。先考虑求7x+4y=1的一个特解。

由7=1×4+3，4=1×3+1，得1=4-3=4-（7-4）=4×2-7，

于是我们得到7x+4y=1的一个特解（-1，2）。进而可得到7x+4y=100的一个特解（-100，200）。而其通解则可以表示为x=-100+4t, y=200-7t（t∈Z）。

这一结果似乎与我们前面得到的结果有差别。这并不奇怪。事实上，二元一次不定方程在无约束条件的情况下，通常有无数组整数解，而由于用不同的方法求同一个不定方程的解时，求出的特解不同，因此，最后得到的通解形式上看上去可能不同。但这种不同只是表面的，当参数取遍一切整数时，它们所包含的全部解是一样的。为了说明这一点，我们也可以将解中的参数做简单的变换，让通解中的特解都取最小解，这样就会容易地看到，各种不同方法得到的通解是完全等价的。

比如对上面的结果，我们令t′=t+25，于是通解可化为更简捷的结果：x=4t′，y=25-7t′（t′∈Z）。显然，这已化为与前面结果相同的形式。

下面再来求一下321x-111y=75的一切整数解。

解：（321，111）=3｜75，所以方程有解。解时可以在方程两边先约去3，得到同解的不定方程107x-37y=25。先考虑解107x+37y=1。

由107=2×37+33　37=33×1+4　33=8×4+1，得

1=33-8×4=33-8×（37-33）=9×33-8×37=9×（107-2×37）-8×37=9×107-26×37，于是得到107x+37y=1的一组特解为（9，-26），由此又可得到107x-37y=1的一组特解（9，26）。进而，我们可以得出107x-37y=25的一组特解为（225，650）。而其一切整数解则可以表示为x=225+37t, y=650+107t（t∈Z）。同样的，这一结果也可以化为与之等价的形式上更简捷的结果：x=3+37t, y=8+107t（t∈Z）。

除上面介绍的方法外，在求解一次不定方程时还有一种通用的方法：连分数法。为了说明连分数法，我们首先介绍一下（简单）连分数的概念。简单连分数，就是具有如下形式的分数：

其中a1是整数（可正可负可为零），a2，a3，a4……都是正整数。a1，a2，a3，……，an称为连分数的部分商。

下面先看看如何才能把一个既约分数化为连分数。实际上，要执行的算法非常简单。我们举几个简单例子演算一下就可以明白了。

通过以上例子，可以发现把既约分数化为连分数的演算方法确实很容易掌握。而通过这种演算最终得到的连分数形式也与演算完全合拍，因而上述的连分数写法非常直观、浅显、一目了然。但一点令人感到不舒服的地方是，从节约纸张的角度来说，这种比较自然的记法太占地方了。于是，人们引入了一种稍简便些的记法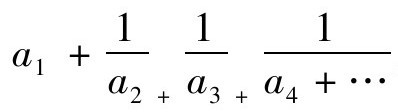：，在第一个“+”号之后所有“+”都写低一些，表示在构造连分数的过程中“降”了一层。再后来，考虑到连分数由其部分商唯一确定，人们索性引入了一种更简便但也更抽象的记法，在这种新记法中，简单连分数直接表示为：[a1，a2，a3，……，an]。如7/4的连分数记为[1，1，3]；4/7的连分数记为[0，1，1，3]；107/37的连分数记为[2，1，8，4]。

在介绍了连分数的记法与化法后，我们需要考虑可以用它来做些什么了。事实上，连分数法现在已经成为一种强有力的数学工具，可以用它来解决许多数学问题。我们这里要介绍的就是用它来求解一次不定方程。

为此，我们要引入渐近分数的概念：连分数[a1，a2，a3，……，an]，在第一、第二、第三……层处切断，再重新化回普通的既约分数，由此得到的这些分数被称为连分数的第一、第二、第三……个渐近分数。以上面的7/4，107/37为例。

由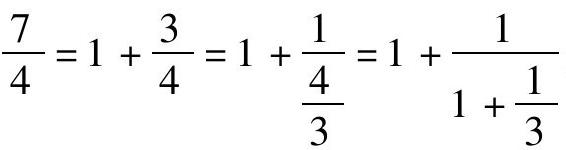，可得到其第一个渐近分数为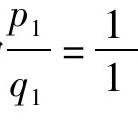，第二个渐近分数为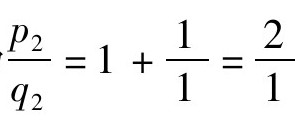，第三个渐近分数为其本身。

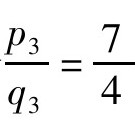同样的，由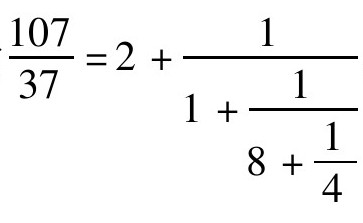，可得到其第一个渐近分数为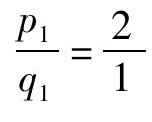，第二个渐近分数为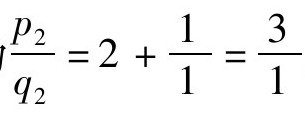，第三个渐近分数为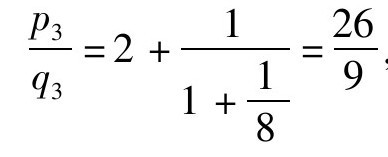，第四个渐近分数为其本身。

用通俗的说法来说这种连分数法求渐近分数的要点就是“丢尾巴，繁化简”。所谓“丢尾巴”就是逐次丢去连分数最下面的分数；然后“繁化简”，把剩下的连分数用化简繁分数的法则化成一个简单分数，这个分数就是渐近分数。

渐近分数具有一些特殊的而且是非常重要的性质，这些性质对人们解决某些数学问题是非常有用的，这正是人们之所以引入渐近分数的原因。下面我们就来看其中的一条性质。

先看7/4的三个渐近分数，，

再看107/37的四个渐近分数，，

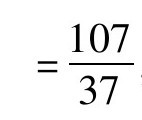事实上，可以证明对渐近分数来说有性质：pkqk-1-pk-1qk=（-1）k，k≥2。

考虑到（pn）/（qn）是最初的分数a/b，于是当k=n时，有aqn-1-pn-1b=（-1）n。这个式子意味着，如果我们能找到a/b的倒数第二个渐近分数（pn-1）/（qn-1），那么我们就能得到ax-by=1（n为偶数）或ax-by=-1（n为奇数）的一个特解。而在此基础上，通过改变符号，就可以得到任何形式二元一次不定方程的一个特解了。

比如说，我们知道了107/37的连分数[2，1，8，4]有四个

（偶数个）部分商，且其倒数第二个即第三个渐近分数，于是应有aq3-p3b=107×9-26×37=1，这样就可以得到107x-37y=1的一个特解（9，26），或得到107x+37y=1的一个特解（9，-26）。

再如，我们知道了7/4的连分数[1，1，3]有三个（奇数

个）部分商，且其倒数第二个渐近分数，于是应有aq2-p2b=1×7-2×4=-1，我们就可以得到7x-4y=-1的一个特解是（1，2）。然后通过改变符号，可得到7x-4y=1的一个特解是（-1，-2）。也可得到7x+4y=1的一个特解为（-1，2）等。

由此，我们可以明白用连分数法求一次不定方程ax±by=1的思路了：把a/b化为连分数，求出它的渐近分数，则（pn-1，qn-1）（或改变一下正负号）就可以提供一个特解。下面我们再举一个例子体会一下这种方法。

求不定方程137x-60y=-10的一个特解。

第一步，把137/60化为连分数得137/60=[2，3，1，1，8]。

下一步是求倒数第二个渐近分数，即求[2，3，1，1]=。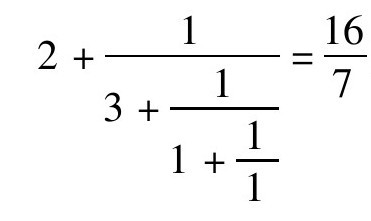

第三步，由137×7-16×60=-1。这样，我们就得到了137x-60y=-1的一个特解（7，16）。而由此易知137x-60y=-10的一个特解为（70，160）。

在对连分数法解一次不定方程的方法做过上述介绍后，下面再补充说明两点。

其一，对一个既约分数化为连分数这一步来说，一种变通的方式是直接利用辗转相除法求各个商即可（由此亦可看出连分数与欧几里得算法的密切联系）。

例如：化107/37为连分数。由107=37×2+33，37=33×1+4，33=4×8+1，4=1×4，各个商数分别为2、1、8、4，于是107/37的连分数形式为[2，1，8，4]。

其二，对第二步求渐近分数，我们还可以得出一种直接的方法。我们简单说明一下。

容易看到，若设正数a的连分数展开式为[a1，a2，a3，……，an]，那么其第一个渐近分数显然是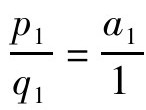：，而第二个渐近分数是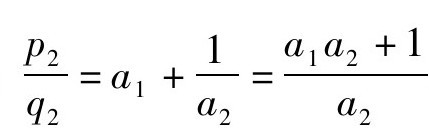：。由此知，p1=a1，q1=1；p2=a1a2+1，q2=a2。而第三个渐近分数算起来稍微复杂一些，经计算会得到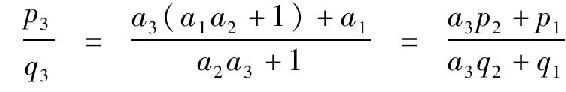。由此，。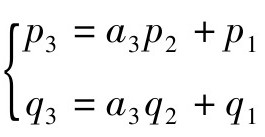

由此可以做出猜测，一般的渐近分数可以用下面的递推公式迅速地算出来。

如果有兴趣，读者可以自己借助于数学归纳法容易地证明这一结论。这一递推公式提供了由前两个渐近分数（它们总是取上面公式中给出的结果）与部分商ai的值求第n个渐近分数的一个简单些的方法。我们以求107/37的第三个渐近分数为例。

首先可求得107/37的连分数为[2，1，8，4]，于是利用上面的递推公式有：

以上所介绍的二元一次不定方程的解法还可以推广到n元一次不定方程。我们先以三元一次不定方程为例。

三元一次不定方程的一般形式为ax+by+cz=d，其中a, b，c为非零整数，d为整数。对此不定方程，显然只有a, b，c的最大公约数（a, b，c）｜d时，它才可能有整数解。而且，同样地可以证明，如果（a, b，c）｜d，那么此不定方程一定有解。简言之，（a, b，c）｜d是此不定方程有整数解的充要条件。至于（a, b，c）的求法，可以先求（a, b）=m，然后再求（m, c），则（a, b，c）=（m, c）。

下面，我们看一下在此类不定方程有整数解的情况下如何求得其整数解。为此，我们通过举一个简单例题说明一下。求方程9x+24y-5z=1000的整数解。

解：先判别一下是否有解。由（9，24）=3，（3，-5）=1，因此（9，24，-5）=1｜1000，不定方程有整数解。

为了求其整数解，先把原三元一次不定方程化为如下的两个二元一次不定方程：9x+24y=3t，3t-5z=1000。其中引入了一个参数t, t前的系数3来自（9，24）。事实上，一般的ax+by+cz=d可化为两个二元一次不定方程ax+by=mt, mt+cz=d，其中m=（a, b）。

在这一步后，一种方法是，先求后一个不定方程即3t-5z=1000的通解，可解得t=2000+5v, z=1000+3v，然后将得到的t的表达式代入前一个不定方程9x+24y=3t即3x+8y=t中，有3x+8y=2000+5v。对这一不定方程，可先得到3x+8y=1的一个特解x=3，y=-1，于是3x+8y=2000+5v的一个特解为：x=6000+15v, y=-2000-5v。这样即可得到3x+8y=2000+5v的通解为：x=6000+15v-8u, y=-2000-5v+3u, z=1000+3v，其中u, v为任意整数。

另一种更方便些的做法是，分别求9x+24y=3t，3t-5z=1000的整数通解，其中在解前面的不定方程时把参数t看成常数。然后在得到的结果中消去参数t，得到的x, y，z表达式即为所求。

具体而言，对9x+24y=3t即3x+8y=t可求得整数通解为：x=3t-8u, y=-t+3u。而3t-5z=1000的通解则为t=2000+5v, z=1000+3v。然后消去参数t，即可得到与上面结果相同的原三元一次不定方程的通解。

类似的，可以考查一般的多元一次不定方程a1x1+a2x2+……+anxn=N（其中a1，a2，……，an，N为整数，n≥2，a1，a2，……，an均不为零）。

首先，与二元、三元一次不定方程的结论类似，一般的多元一次不定方程有整数解的充分必要条件是（a1，a2，……，an）｜N。而其求解思路仍然是：将此n元一次不定方程化解成n-1个二元一次不定方程组：a1x1+a2x2=m1t1，m1t1+a3x3=m2t2，……，mn-1tn-1+anxn=N，其中m1=（a1，a2），m2=（m1，a3）……然后分别求出这些二元一次不定方程的通解，其中会出现n-1个参数；联立这些表达式，并消去所有的参数即可得到多元一次不定方程的通解。

在介绍了几种现代解决一次不定方程的方法后，我们打算回溯历史，看一下古代人是如何做的。我们的目光将主要放在古印度人身上，因为是他们较早并彻底地解决了这一问题。

在第一编中我们已经提到，古印度数学发展的鼎盛繁荣时期是5世纪～12世纪。在这期间，印度出现了许多有代表性的数学家。这里，我们先介绍其中的一位：阿耶波多。

阿耶波多（Aryabhata，476～550）是迄今所知最早的印度数学家。他的唯一传世之作是《阿耶波多历数书》（499）。全书分四部分，由121节诗组成。用诗的形式编排内容，便于口头传诵，是印度当时写作最常用的形式。他的这本写于23岁的早期著作是印度最早的一本有明确作者的完整的数学、天文学论著，这使它显得格外突出并在印度及阿拉伯国家产生了持久的影响。

1975年4月19日，为表达对他所取得成就的肯定与敬意，印度把自己组装并通过前苏联成功发射的第一颗人造卫星命名为“阿耶波多号”。

阿耶波多

作为印度数学史上第一位知名数学家，阿耶波多确实对数学作出了多方面的贡献。他在其书《阿耶波多历数书》的第二部分共用33节诗专论数学，内容涉及算术、代数、几何、三角及不定分析等知识。其主要成就包括开创弧度制度量等。特别是，他开古印度一次不定方程研究之先河，并创造了具有浓郁印度特色的库塔卡方法。一般认为，用这一方法求解一次不定方程是他在数学上作出的最大贡献。

阿耶波多最初思考的问题是：如何决定一个整数N，使N除以整数a余r1，除以整数b余r2。显然，由N=ax+r1=by+r2，我们可得到一次不定方程：ax+c=by，其中c=r1-r2。通过研究，阿耶波多给出了求解这类不定方程通解的法则：库塔卡法。库塔卡是梵文，其意是“粉碎”或“碾细”，因此库塔卡法也常译为“粉碎法”或“碾细法”。我们下面简单介绍一下这种方法，由此可以体会这种方法名称的由来。

为求方程ax+c=by的整数解，首先对a、b使用辗转相除法。因为要解的不定方程我们假设了a, b互素，所以在相除的过程中，一定会出现余数是1的情况，操作进行到此时停止，于是可得到系列商｛q1，q2，q3，……，qn}，以及相应的余数系列｛r1，r2，r3，……，rn=1}。

下一步，先求解不定方程rns±c=rn-1t，其中rn=1，rn-1表示倒数第二个余数。而如果系列商的个数为偶数，则不定方程取“-”，系列商的个数为奇数，则不定方程取“+”。显然这个不定方程的一个特解可以非常容易地得到。

最后一步，利用得到的这个特解，逆推回去，得到原不定方程ax+c=by的一个特解。为了简化这一步，阿耶波多引进了一种表格。对此，我们可以通过例题体会。下面我们就举几个例子来看一下他的方法。

例：求解不定方程137x+10=60y。

解：先做辗转相除

137=2×60+17，

60=3×17+9，

17=1×9+8，

9=1×8+1

这样得到一个系列商：2、3、1、1，共有4个商；余数系列：17、9、8、1。

下一步考虑求不定方程1s-10=8t的一个特解。其中，系数1是上面辗转相除最后一步得到的余数；系数8是上面辗转相除倒数第二步得到的余数；取减号是因为商的个数是偶数。

显然，1s-10=8t的特解非常易求。比如，我们令t=1，则可得s=18。这样就得到了1s-10=8t的一个特解（18，1）。随后，阿耶波多所做的就是由这一个特解，逐步递推回去，直至得到原不定方程137x+10=60y的一个特解。为了使这一步演算起来方便，他借助了下面的表格。我们解释一下这一表格是如何得出的。

先把系列商及得到的18、1排成一列（商自上而下排列，然后是s值，最后是t值）。然后，18乘以它上面的数（此处为1），然后加它下面的数（此处也为1），得19，用这个数替换掉18上面的数，同时去掉它下面的数，其他数保持不变。于是原来的一列数变为它后面的一列数（即下表中的第二列数）。对新得到的这列数执行同样的操作：19乘以它上面的数（此处是1），然后加上它下面的数（此处是18），得37，用这个数替换掉19上面的数，同时去掉19下面的数，其他数保持不变。于是由第二列数得到第三列数。连续进行这一操作，直到只剩下两项时为止。这样得到的最后两个数就是我们要找的特解，其中x=130，y=297。

阿耶波多给出的方法还有更灵巧之处。他指出，当我们在做辗转相除时不一定非要做到余数为1。比如，对上面题目在做辗转相除时，假设我们做到如下一步：

137=2×60+17，

60=3×17+9，

17=1×9+8，

这样得到一个系列商：2、3、1，共有3个商；余数系列：17、9、8。

下一步考虑求不定方程8s+10=9t的一个特解。其中，方程左边系数8是上面辗转相除最后一步得到的余数；右边系数9是上面辗转相除倒数第二步得到的余数；取加号是因为商的个数是奇数。

对8s+10=9t而言，若令t=2，则可得s=1。于是我们得到一个特解（1，2）。然后，我们在此基础上列表递推回去，所得到原不定方程137x+10=60y的一个特解：x=10，y=23。

继续试一下。假设在做辗转相除时，只做到：

137=2×60+17，

60=3×17+9，

这样得到一个系列商：2、3，共有2个商；余数系列：17、9。

下一步考虑求不定方程9s-10=17t的一个特解。其中，方程左边系数9是上面辗转相除最后一步得到的余数；右边系数17是上面辗转相除倒数第二步得到的余数；取减号是因为商的个数是偶数。

对9s-10=17t而言，若令t=1，则可得s=3。于是我们得到一个特解（3，1）。然后，我们在此基础上列表递推回去，可得到原不定方程137x+10=60y的一个特解：x=10，y=23。

下面我们再举上面介绍过的几个例题说明一下这种方法。

求不定方程7x+4y=100的一个特解。

解：我们对此可以先求7x-100=4y的一个特解。

由7=1×4+3，4=1×3+1，可得到系列商：1、1。余数系列：3、1。

商的个数是偶数，最后的余数是1，倒数第二个余数是3。于是我们可以先求解不定方程1s-（-100）=3t，令t=34，得s=2。于是系列商加上2、34可得到第一列数。然后对这列数进行上面介绍的操作，最后可得到7x-100=4y的一个特解：x=36，y=38。

由此，我们可以得到7x-100=-4y（即原不定方程7x+4y=100）的一个特解：x=36，y=-38。

继续求不定方程107x-37y=25的一个特解。

解：由107=2×37+33，37=1×33+4，33=8×4+1，得系列商：2、1、8；余数系列：33、4、1。

商的个数是奇数，最后的余数是1，倒数第二个余数是4，因此我们需要先求解1s+（-25）=4t，令t=-6，得s=1。于是把系列商与1、-6排成一列数。然后对这列数进行上面介绍的操作，最后可得到107x-25=37y的一个特解：x=3，y=8。

通过上面两个例子，我们看到，即便ax+c=by中的c为负，也可以直接利用这种方法求特解。另外，在上面的例子中，都是a>b，如果出现a<b时如何解决呢？我们举下面例子说明一下。

求8x-4=29y的一个特解。

解：先做辗转相除

8=0×29+8

29=3×8+5

8=1×5+3

5=1×3+2

3=1×2+1

得系列商：0、3、1、1、1。后面两个余数：1、2。

因为商的个数是奇数，最后的余数是1，倒数第二个余数是2。于是我们可以先求解不定方程1s+（-4）=2t，令t=0，得s=4。于是系列商加上4、0可得到第一列数。然后对这列数进行上面介绍的操作，最后可得到8x-4=29y的一个特解：x=44，y=12。

通过上面的介绍，我们看到用阿耶波多的方法确实可以有效地找到ax±c=by（a, b，c都是正整数）的一个特解。当然，由于具体求的步骤的差别，最后得到的特解并不一样。但正如我们已经指出的，不管特解如何取，最终得到的全部解是相同的。另外，我们也提到，如果我们选取合适的参数，使特解都转化为最小特解，那么这个最小特解是唯一的。对这种转化如何进行，我们也已经简单介绍过。这里不再赘述。事实上，阿耶波多就已懂得了转化的方法。

进而，阿耶波多还将其方法推广到解一次联立不定方程组。如他研究并解决了不定方程组。这些研究都走在了当时世界前列。