几何三大作图问题

几何三大作图问题

在几何学中，作图问题是人们喜欢的一个课题。只用圆规和直尺就可以完成许多作图问题，例如二等分一条线段或一个角、过一点作一给定直线的垂线、作圆内接正六边形等等。在所有这些问题中，直尺仅仅当作一直边，一个画直线的工具，而不能用于测量或标示距离，是一个没有刻度的直尺。只限于用圆规和直尺作图的习惯是古希腊人流传下来的，它具有一定的理论意义和方法论意义，是研究问题的一种方法。实际上希腊人在作图时也毫不犹豫地使用了其他工具。

数学上有许多这样的问题，问题本身很简单，是属于初等数学问题。但是要想从逻辑上彻底解决它们，却受到人的认识能力的限制。在知识水平和数学方法还没有发展到一定程度之前，这些问题无法彻底解决。也许正是因为如此，这些问题刺激了许多学者投身研究。尽管在一定的历史时期这些问题是不可能做出的，但是研究过程中产生了许多新学科、新方法，为数学发展注入了新的活力和生命力。例如费尔玛大定理、寻求五次一般方程的根式解等属于这一类问题，还有一个“几何三大作图问题”也属于这一类问题，而且这个问题经历了2000多年时间才最后解决。另外，这个问题虽然是几何问题，但最后却是因为代数学的发展才得以解决的。这也说明了数学这门古老而又富有生命力的学科的统一性。

什么是“几何三大作图问题”

几何三大作图问题是:(1)倍立方:求作一个立方体，使其体积是一已知立方体的二倍;(2)三等分任意角;(3)化圆为方:求作一正方形，使其面积等于一已知圆。在所有这些问题中，只允许用圆规和直尺。这里需要说明的一点是，处理几何作图问题，不是要求以一定的精确度实际把图画出来，而是从理论上说明只用圆规和直尺能否找出画图的方法来。其次，还要说明，在这里几何作图的概念在某种意义下似乎是人为的。圆规和直尺肯定是作图的最简单的工具，但是在几何中从来没有只限于用这些仪器。如果允许使用直尺、圆规以外的作图工具，如直角三角板或半圆尺等，这三大作图问题就很容易解决，早在古希腊时代就已经被解决。因此，这样一个看似不经意的限制条件却是一个十分重要的条件。

“几何三大作图问题”的历史起源

古希腊是世界文化、科学的发源地之一。数学也是古希腊最为发达的学科之一。在数学史上，希腊数学一般指从公元前600年—600年间活动于希腊半岛、爱琴海区域、马其顿与色雷斯地区、意大利半岛、小亚细亚以及非洲北部的数学家所创造的数学。

公元前5世纪上半叶，历史上著名的希波战争以后，希腊数学开始走向繁荣。具体表现是产生了许多学派，其中有一个著名的巧辩学派，也叫“智人学派”、“诡辩学派”或“哲人学派”。这个学派以提出并致力研究“几何三大作图问题”而著称。

关于倍立方问题，埃拉托塞尼(约公元前276—前195年)在他的《柏拉图》一书中记述了一个传说，后来被赛翁(约390年)所用并流传下来。说是鼠疫袭击提洛岛，一个先知者得到神的谕示向提洛岛的人宣布，必须将现有的立方体祭坛的体积加倍，瘟疫方可停息。工匠们试图弄清怎样才能造成一个立方体，使其体积为另一个立体的2倍。为此他们陷入深深的困惑之中，于是他们就这个问题去请教柏拉图。柏拉图对他们说:神的真正意图不在于神坛的加倍，而是想使希腊人为忽视几何学而感到羞愧。

第二个是三等分任意角。用尺规去二等分一个角是轻而易举的，自然会提出三等分任意角的问题。另外，在历史上，除了“几何三大作图问题”外，还有正n边形的尺规作图也是此类问题。而如果任意一个角能用尺规作其，那么诸如正9边形、正18边形就可由正三角形得到。

圆和正方形都是最常见的几何图形，也是古代人最早认识的几个图形之一。因而，自然会想到可否作一个正方形和已知圆等积。这就是化圆为方问题。在历史上，化圆为方问题强烈地吸引了人们的兴趣。巧辩学派中的安蒂丰(约公元前5世纪人)由于研究化圆为方而提出了一种“穷竭法”，是近代极限思想的起源。他提出的“穷竭法”解决化圆为方的问题被亚里士多德记载在《物理学》一书中流传下来。安蒂丰的穷竭法，是先作圆内接正方形(或三角形)，将边数加倍，得内接正八边形、十六边形、三十二边形。这样继续下去，他深信到“最后”，正多边形必与圆重合，也就是多边形与圆的“差”必会“穷竭”，于是便可以化圆为方了。这种方法虽然不能解决化圆为方问题，却提供了一种求圆积的方法，也即得到了一种计算π的方法。

这三大问题根本不可解

经历了若干世纪，数学家们毫无所获地寻求着这些问题的解法，后来逐渐怀疑这样问题可能根本就不可解。但是“如何才能证明某些问题是不可解的呢?”数学家遇到了挑战。

现在看来，这样一个看似很简单的初等几何问题是不可能在初等几何范围内解决的。在17世纪费尔玛和笛卡尔发明了解析几何之后，为数学家解决这三大问题提供了一个很好的工具。借助这样一种“几何与代数”统一的思想，为了更清楚更深刻地理解作图问题，我们可以将几何问题“翻译”成代数语言。于是任何一个几何作图问题都是这种类型的:给定某些线段如a，b，c，…，求一个或多个其他线段x，y，…几何作图问题实际上就是已知一些几何量，去求作另一些几何量。为简单起见，假设只需求作一个线段x。于是几何作图就归结为解一个代数问题:首先，我们必须找出所求的量x和给定的量a，b，c，…之间的关系(方程);其次，必须解这方程来求未知量x;最后，我们必须确定，通过相应于用圆规和直尺来作图的代数过程能否得到这个问题的解。三大问题不可解的思路逐渐清楚起来了。

下面要做的就是将这三大问题“翻译”成代数思维:

(1)倍立方体问题:设给定的立方体的边是单位长，则它的体积是一立方单位。如今要求出一个体积是它的2倍的立方体的边长x。于是所求边长x满足一个简单的三次方程x³－2=0于是，我们的问题是数x=是否能用直尺和圆规做出。

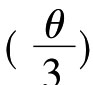(2)三等分任意角:可以用各种不同方式，来得到这个问题的代数等价问题。最简单的是考虑由余弦cosθ=g给出的角θ。这时问题等价于求量x=cos的问题。应用三角公式可知cosθ=g=4cos³－3cos，令cos=z，则有4z³－3z=g即4z³－3z－g=0…

于是三等分任意角的问题就转化为以上方程的根是否能用尺规做出的问题。

(3)化圆为方:设圆的半径是一个单位，那么面积就是π。因此作一面积等于单位圆的正方形，相当于求作一条长为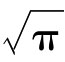的线段，这个线段将是所求正方形的边。于是化圆为方问题就转化为是否可用尺规作图的问题。

由以上讨论，我们可以看出，几何三大问题都归结为一些数能否用尺规做出的问题。因此，我们必须去解决的一个问题是:能用尺规做出的数具有什么特性。即什么样的数或数的集合能用尺规做出。

什么样的数可用尺规做出

讨论了三大几何作图问题的本质之后，这三大问题的可解性就转化成去刻化尺规可作图的数的基本特征了。

“有理”的代数过程——已知量的加、减、乘、除能用尺规作图来实现。

如果给定两个长为a和b的线段，可以做出a+b，a－b，ra(r是任意有理数)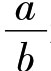，和ab。

作法:a+b

画一条直线，在上面用圆规标出距离OA=a，AB= b，则OB=a+b。

a－b

画一条直线OA=a，在OA上用圆规截AB=b，则OB=a－b。

能作加法，就能做出pa，p是任意正整数，只要作连加即可。

下面作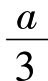，在一直线上标出OA=a，过O任意作第二条直线，在直线上我们标出任一线段OC=c，再作OD=3c。连接AD且过C画一直线平行于AD，交OA于B，则OB=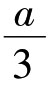。用同样的方法我们能画出，q是任一正整数。令r=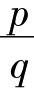，则同理可做出，然后再作p，就有ra。r为任一有理数。

为了作，在任意一个角O的两边标出OB=b，OA=a，且在OB上标出OD=1，过D作平行于AB的直线交OA于C，则OC的长为a/b。

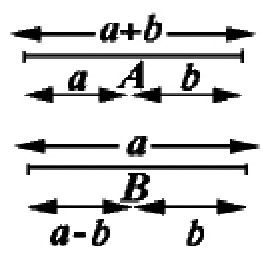
图3-2　a+b与a-b

图3-3　a/3

图3-4　a/b

图3-5　ab

最后作ab，在任意一个角O的两边上标出OA=a，OC=b，OB=1，连接BC，过A作平行于BC的直线AD交OC的延长线于D，则OD=ab。

由以上作图可知，已知量的加、减、乘、除运算都能用直尺和圆规做出。自然就会再深入一步:一个已知量的平方根能否用直尺和圆规做出呢?也能，如果给定一个已知线段a，则可只用圆规和直尺作

作法:在直线上标出OA=a，AB=1。以OA为直径作一圆，而且过A作OB的垂线交这个圆于C。

则AC²=OA·AB=a，AC=

假设最初只给定了一个元素，即单位长1。则由以上讨论可知，我们用圆规和直尺能做出由单位长通过有理运算加减乘除而得到的所有数，即所有有理数，这里r与s为整数(s≠0)。在数学上，如果一个数集关于加减乘除四种有理运算封闭，就称为一个数域。

图3－6

的作图

于是从这个单位出发，我们就能用尺规做出整个有理数域，因而做出坐标平面上的所有有理点(即坐标为二个有理数的点)。另外，我们还能做出有理数域中所有正有理数的平方根，因此，对于数域F，任取其中的数a、b、c(c＞0)，则可用尺规做出所有形如a+ b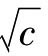的数，而所有形如a+ b的数也对加减乘除封闭，即任意两个形如a+ b的数通过加减乘除运算之后仍然是形如a+的数。因此，这样的数也构成一个域，如果称有理数域为F₀，则形如a+ b的数集形成一个域F₁，而且域F₀称为域F₁的子域。

所有可作图的量的全体，现在能够确切地描述了。无论最初给定了一些什么量，从由它们确定的一个给定域F₀出发。例如，如果只给定一个线段作为单位长，那么，它所确定的是有理数域，然后添加属于F₀，但不属于F₀，我们能做出可作图量的一个扩域F₁，它由所有形如a₀+b₀的数组成，其中a₀、b₀可以是F₀中的任意数。进一步作F₁的一个新的扩域F₂，它由形如a₁+b₁的数组成，其中a₁、b₁，是F₁中的任意数。而k₁是F₁中的某个数，它的平方根不属于F₁。重复这个过程，在n次加进平方根以后，我们能得到一个域F_n。可作图的量是而且仅仅是那些能用这样一系列扩域达到的数(即属于上述类型的域F_n)。扩充的个数n取多大这是无关紧要的，在某种意义上它标志着问题的复杂程度。

下面我们用一个例子来说明这个过程。从理论上说明以下数可用尺规做出。

设F₀是有理数域，取k₀=2，我们得到域F₁，它包含了数1+现在取k₁=3，a₁=1+，b₁=1，则1+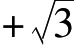属于域F₂。最后取k₂=5，同理，我们得到域F₂，F₂包含了数1+再取k₃=1+我们得到域F₃，F₃包含数因而对于F₀通过3次扩域而得到了数可用尺规做出。

三大问题的不可解性

由本节(3)中的讨论，我们已经得出，倍立方问题的可解性由x=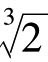是否能用尺规作图决定。现在可用反证法来证明x只用圆规和直尺是不能做出的。

证明:假设是可以用尺规做出的。

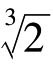因为是一无理数，所以不能属于有理数域F₀，因此只能属于某个扩域F_K，K∈N假设K是使得扩域F_K包含x的最小正整数。

故可设x=p+q的形式，

其中p，q，ω∈F_k－1，但现在我们来说明，如果x=p+q是三次方程x³－2=0的一个根，则x= p－q也是它的一个根。

∵x∈F_k，∴x³∈F_k，x³－2∈F_k

对此(1)与(2)式可得a=p³+3pq²ω－2，b=3p²q+q³ω

如果令y=p－q然后在a，b的表达式中以－q代替q，就得至y³－2=a－b√ω

∵　　x³－2=0

∴　　a+b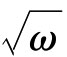=0

由此可得出=－∈F_k－1与假设矛盾。

因此必有a=b=0

则有a－b

所以y=p－q也是方程x³－2=0的一个根。且x≠y。否则x－y=2q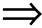q=0=0

∴　　x=p∈F_k－1与假设矛盾。

我们得出x=p+q如果是三次方程x³－2=0的一个根，则y=p－q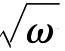是该方程的另一个根。而对于三次方程x³－2=0来说，它只有一个实根，其余两个根是虚根。而p±q都是实数，得出矛盾。因此x³－2=0的根不能在域F_k中，所以用直尺和圆规作倍立方体是不可能的。

利用以上思路，容易证明:

如果一个有理系数的二次方程没有有理根，则它的根没有一个是由有理数域F₀出发的可作图的数。

利用以上结论和本节(3)中的讨论，我们只要说明三次方程4z³－3z－g=0没有有理根，即可说明三等分任意角的不可能性。

不妨取θ=60°，则g=cos60°=，方程变为

8z³－6z=1

设u=2z

就有u³－3u=1　……………………………………(1)

假设方程(1)存在有理根u=r/s满足这个方程，

(r，s)=1

代入(1)式有

r³－3s²r=s³

s³=r(r²－3s²)

∴r|s³继而r|s必有r=s=1，否则与(r，s)=1矛盾。

因此r=s=±1代入(1)式不满足方程，从而方程(1)，即方程8z³－6z=1没有有理根。

这就证明了三等分任意角只有尺规是不可能的。

我们已经用比较初等的方法处理了倍立方、三等分任意角问题。但是三大问题中的最后一个化圆为方比较复杂一些，需要用数学分析的方法方能说明。

化圆为方最后归结为π是否可尺规做出，即需要说明π不能包含在由有理数域F₀连续添加平方根而达到的任意域F_n中。在18世纪时，数学家猜测存在一种类型的无理数，不满足任何有理系数代数方程，这种数就是超越数，而满足有理系数代数方程的数叫代数数。19世纪时，在1882年，林德曼证明了π是超越数，从而证明了π不可以用尺规作图这一问题。

由此，一个在公元前5世纪被提出的三大几何作图问题到了公元1882年，在经历了2000多年的探索之后最终得以解决。

【注释】

[1]李继闵著。《九章算术》导读与译注。陕西科学技术版社，1998，626页。

[2]同①。

[3]同①，388页。

[4]吴文俊主编。世界著名学家传记(上)。科学出版社，1995，395页。

[5]同④，403页。

[6]邓明立，伽罗瓦，吴文俊主编。世界著名数学家传记(上册)。科学出版社，1995，924页。

[7]费尔玛著，高嵘译。论解析几何。——李文林主编。数学珍宝。科学出版社，1998，514页。

[8]同⑦，515页。