平面反射系统中物像关系的矩阵表示方法

5.8　平面反射系统中物像关系的矩阵表示方法

在研究矢量计算方法的基础上，类似于第4章矩阵方法在共轴球面系统近轴光学中的应用，本节将讨论用矩阵工具研究平面反射系统物像空间方向上共轭关系的基本方法和概念。

平面反射系统的成像作用，从数学意义上理解，是在一个三维线性空间（欧氏空间）进行的线性变换，它满足线性变换的一般规律，当选定基底后，其变换可用线性方程组来表示；应该着重指出的是，平面反射系统对物像的变换作用是一种特殊的线性变换——正交变换，即变换前后它保持向量的内积不变。若设m表示欧氏空间V₃中的正交变换，则对任意的两个向量A，B∈V₃，均有

（mA，mB）=（A，B）

由此，可导出变换前后向量的长度和夹角不变，即：长度：│mA│=│A│；夹角：〈mA，mB〉=〈A，B〉，式中A≠0，B≠0。

特别，若A⊥B，则mA⊥mB。上述特性在平面反射系统成像中的具体体现是，变换前后物像的大小恒不改变。

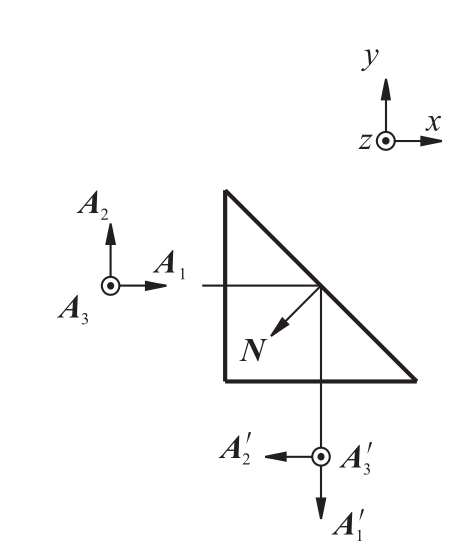
为了研究平面反射系统的物像共轭关系，首先确立如图5.48所示的右手直角坐标系O－XYZ作为标准坐标系。选取分别与X、Y、Z轴一致且彼此相互垂直的单位矢量A₁、A₂、A₃代表物空间的三维物体。其中，A₁沿入射光轴方向；A₂、A₃代表物平面，A₃垂直于图平面指向读者，A₂在图平面内并与A₁、A₃构成右手直角坐标系。物坐标基底（简称物基）i、j、k为标准正交基。经平面反射系统所成像的方向用A₁＇、A₂＇、A₃＇表示。其中，A₁＇沿出射光轴方向；A₂＇、A₃＇平面为像平面，像坐标基底（简称像基）i＇、j＇、k＇亦为标准正交基。

图5.48表示了具有同一光轴截面的平面反射系统物像方向共轭关系的示意图。实际上的平面反射系统光轴也可能为空间折线，因此将有更复杂的情况。严格说，平面反射系统的物像共轭关系，应该包括位置上的共轭关系和方向上共轭关系。从实用的意义考虑，我们主要关心它们在方向上的共轭关系，而不注意它们的位置。因此图中的像坐标A₁＇、A₂＇、A₃＇与物坐标A₁、A₂、A₃只具有方向上共轭的意义。一般情况下，是研究物空间的单位矢量A在像空间与之共轭的单位矢量A＇的确定方法。这里，A是广义的物矢量，它可以是任意的光线矢量、光轴矢量、物面的坐标矢量以及反射面法线、角镜棱线等特征矢量；同样，A＇也是广义的像矢量。在研究上述平行光路中平面反射系统的物像方向共轭关系时（包括平行光路中的光轴问题及像倾斜问题），所涉及的矢量均为自由矢量（即在空间可沿任意方向平移的矢量）。

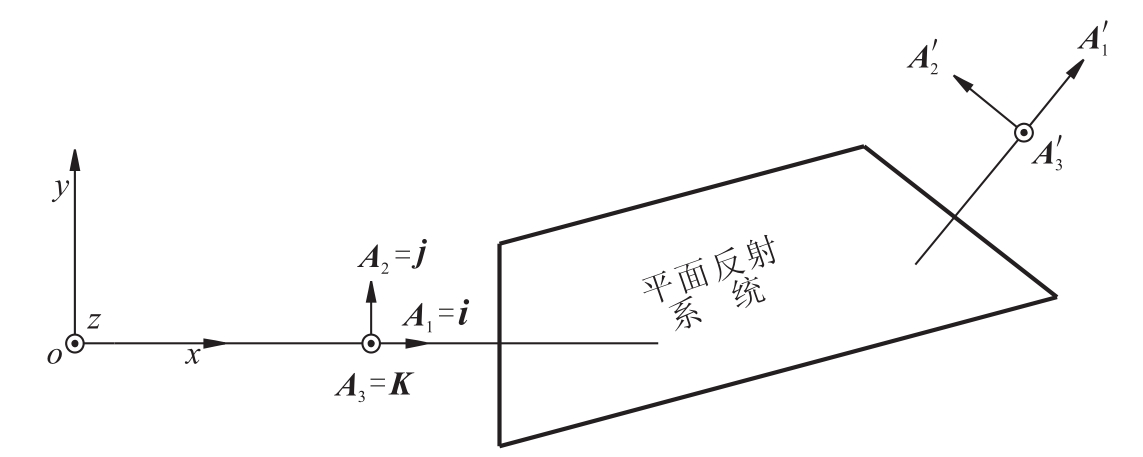
图5.48　具有同一光轴截面的平面反射系统物像共轭关系

下面，重点介绍与平面反射系统正交变换相对应的平面反射系统作用矩阵的概念及其确定方法。

从一般情况出发，设m是平面反射系统在标准正交基i、j、k下的一个正交变换，单位物矢量A及其共轭的单位像矢量A＇的坐标分别为：A_x、A_y、A_z和A_x＇、A_y＇、A_z＇，则变换m可以表为如下的线性方程组形式：

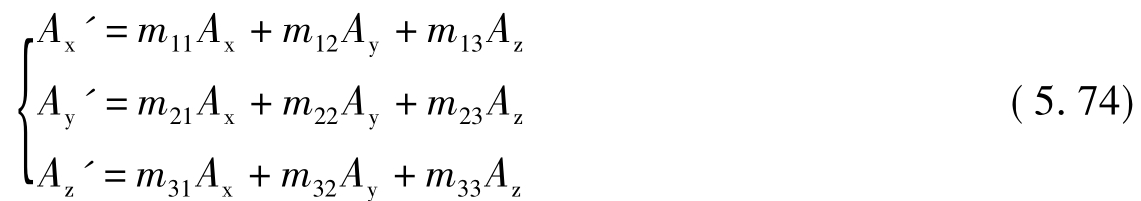
上式亦可写为如下矩阵方程的形式：

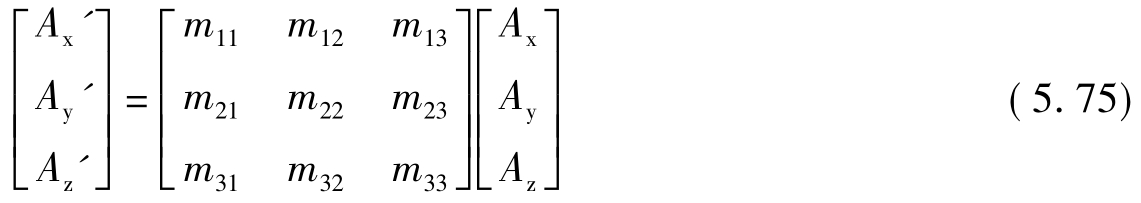
上式中分别为矢量A＇和A的列矩阵形式。此外，定义

将上述表示形式代入式（5.75）则有

A＇=MA　　　　　　　　　　　　　　　　　（5.77）

式（5.75）和式（5.77）即为平面反射系统物像方向共轭关系的表达式，式中的三阶方阵M代表了欧氏空间V₃内的一个正交变换作用，因此定义M为平面反射系统的作用矩阵。显然，在标准正交基下，对应于正交变换的方阵M为正交方阵（矩阵）。本节中涉及有关正交矩阵的部分重要性质有：

（1）正交矩阵M的行列式值detM=±1；

（2）正交矩阵M的非奇异阵存在逆矩阵，其逆阵也是正交矩阵；

（3）正交矩阵的逆阵等于其转置矩阵，即M^－1=M^T；且有M^TM=MM^T=E，式中E为单位方阵。

（4）正交矩阵的乘积仍为正交矩阵。

（5）正交矩阵M的n个列矢量（或n个行矢量）是两两正交的单位矢量。其任意一行或任意一列的每个元素的平方和等于1；任意两行或任意两列中对应元素乘积之和等于零。正交矩阵元素间的这种性质又称为正交条件。

确定平面反射系统作用矩阵的常用方法有如下两种：（1）利用平面反射的矢量计算公式与矩阵乘法求得；（2）根据标准正交基的成像变换结果求得。以下分别具体介绍：

1）利用平面反射的矢量计算公式与矩阵乘法计算平面反射系统作用矩阵

平面镜是平面反射系统的基本组元，而且分析表明，很多平面反射系统均可简化为一等效的平面镜。因此，有必要首先研究平面镜的作用矩阵。

若物矢量A、反射面法线矢量N和像矢量A＇在标准坐标系o－xyz中的各分量分别为： A_x、A_y、A_z；N_x、N_y、N_z；A_x＇、A_y＇、A_z＇，将它们代入（5.58）式，即A＇=A－2（A·N）N，则可得到如下线性方程组的形式：

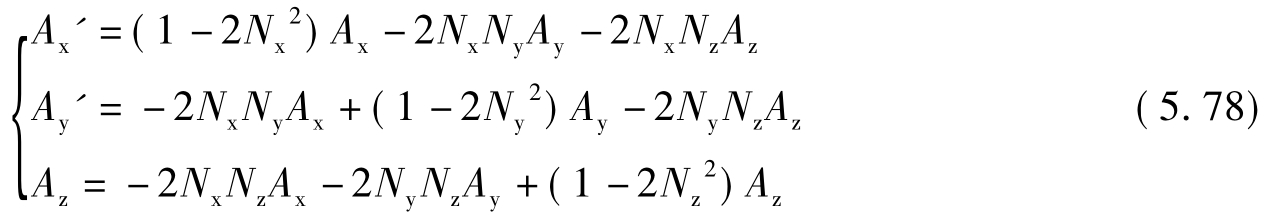
上述三元一次线性方程组若以矩阵方程形式表示，则为：

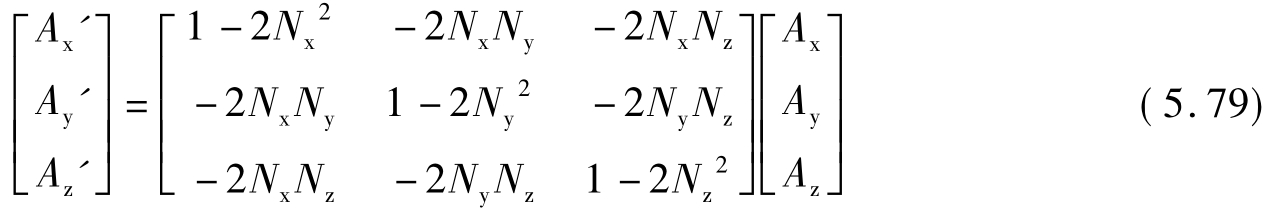
上式中，令

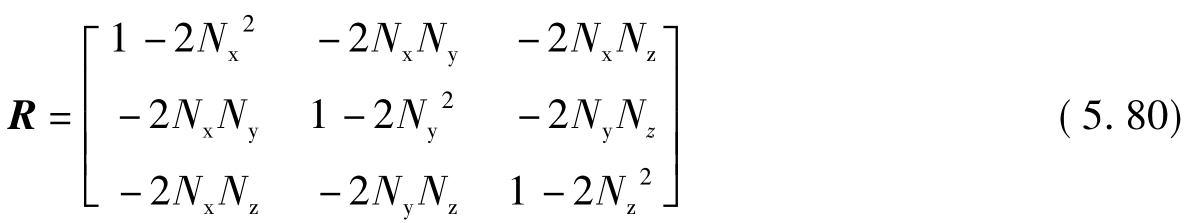
可称此三阶方阵R为平面镜的“反射矩阵”，它也就是平面镜的作用矩阵M。

这样，当给定平面镜在标准坐标系中的空间方位，即知道N的三个分量N_x、N_y和N_z后，代入式（5.80）即可求出平面镜的作用矩阵M，进而由式（5.79）计算像矢量A＇。

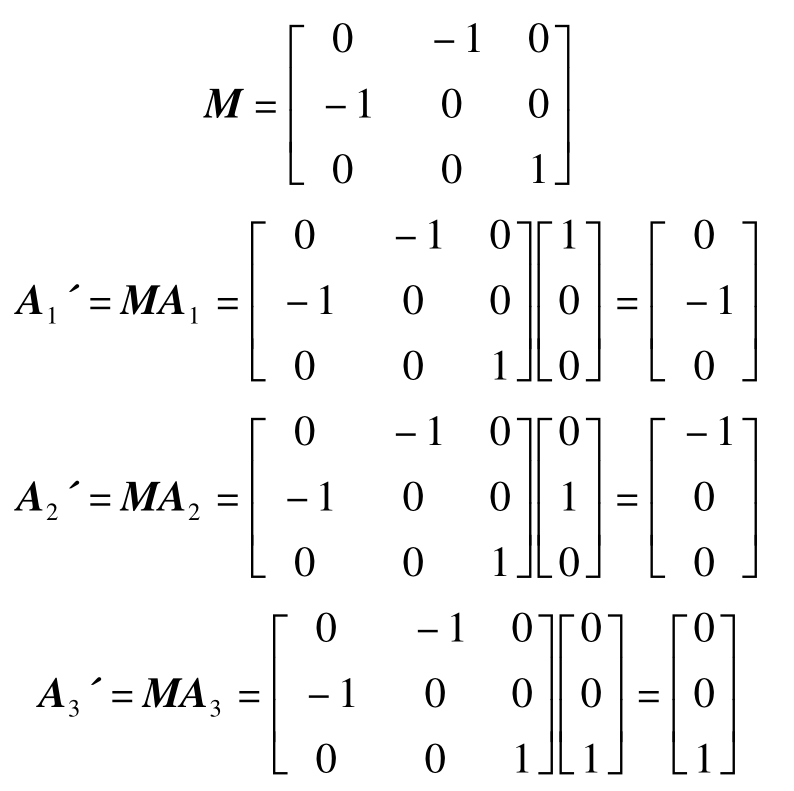
［例5.3］　计算如图5.49所示的物矢量A₁=i，A₂=j，A₃=k（标准正交基）经直角棱镜DI－90°后的像矢量A₁＇，A₂＇，A₃＇。

［解］：由图5.49知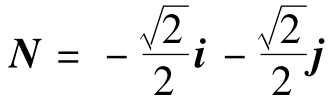，，即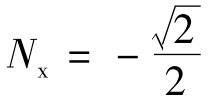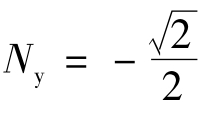，，N_z=0，将其代入式（5.80），则得到作用矩阵，并可求出各像矢量。

5.49　DⅠ－90°直角棱镜的物像变换

计算结果为：A₁＇=－j，A₂＇=－i，A₃＇=k，即成镜像。

在统一的标准坐标系o－xyz内，若平面反射系统由n个反射面组成，则反映其综合作用的作用矩阵M，应由n个反射矩阵的有序乘积构成，即：

M=R_n·R_n－1·…R₂·R₁　　　　　　　　　　（5.81）

式中每个反射面的反射矩阵均由式（5.80）求得。

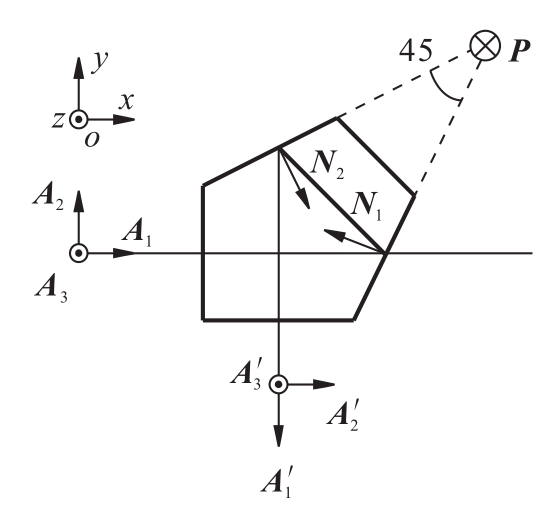
图5.50　五棱镜的作用矩阵

特别，对二面角镜应有

M=R₂·R₁（5.79）

［例5.4］　计算如图5.50所示五棱镜（DⅡ－90°）在标准坐标系o－xyz下的作用矩阵。

解：如图所示，N₁=－cos22.5°i+sin22.5°j

即N_1x=－cos22.5°；N_1y=sin22.5°

又N₂=cos67.5°i－sin67.5°j

即N_2x=cos67.5°，N_2y=－sin67.5°

分别代入式（5.80），得到

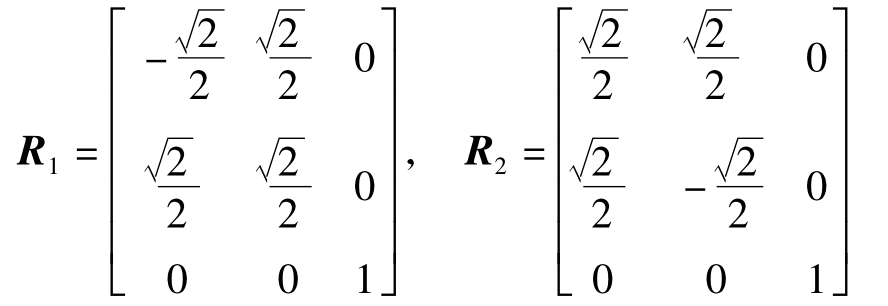
五棱镜作用矩阵

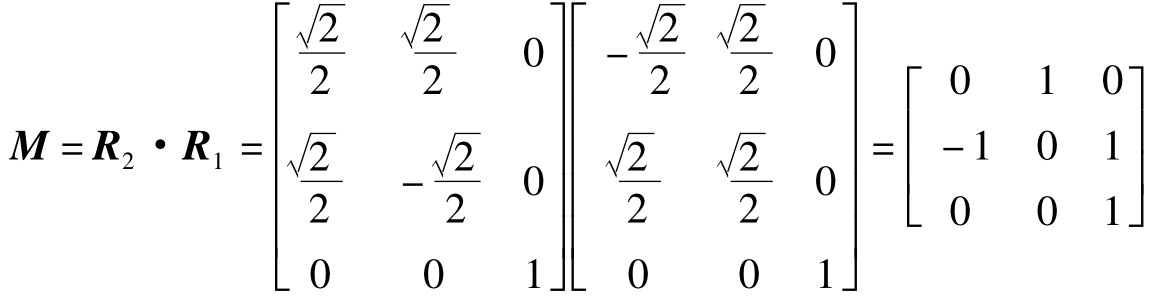
角镜的作用矩阵也可由二面角镜的反射公式（5.71）直接得到。

A″=Acos2α+（1－cos2α）（A·P）P－sin2α（A×P）

在标准坐标系o－xyz中，若A、P、A″的坐标分别为：A_x、A_y、A_z；P_x、P_y、P_z和A_x″、A_y″、A_z″，则代入上式并经整理后应有：

因此，二面角镜的作用矩阵一般表达式为

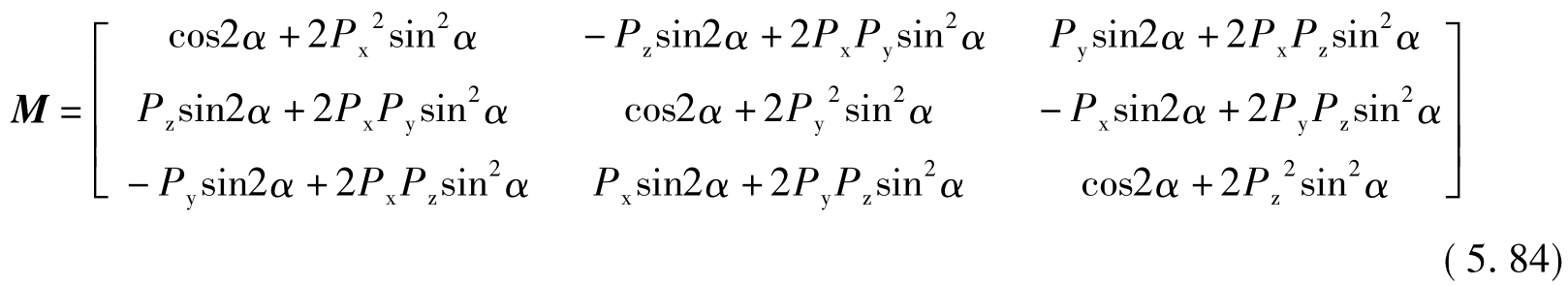
常用如下的特别情况，如P_x=0、P_y=0、P_z=1（P=k），则有

应该注意的是，上述各式中的2α（=ω）系指从入射光线到出射光线按右手定则所转过的角度，它与角镜的两个反射面相对于入射光线的位置有关。如果从入射光线到出射光线的转角是按右手定则，绕－Z轴转成，则式中所有的2α应以－2α取代。这一事实也表明，平面反射系统的作用矩阵与系统和入射光轴的相对位置有关。图5.51表示了应用式（5.85）所得到的两种不同情况下的五棱镜作用矩阵（α=45°）。

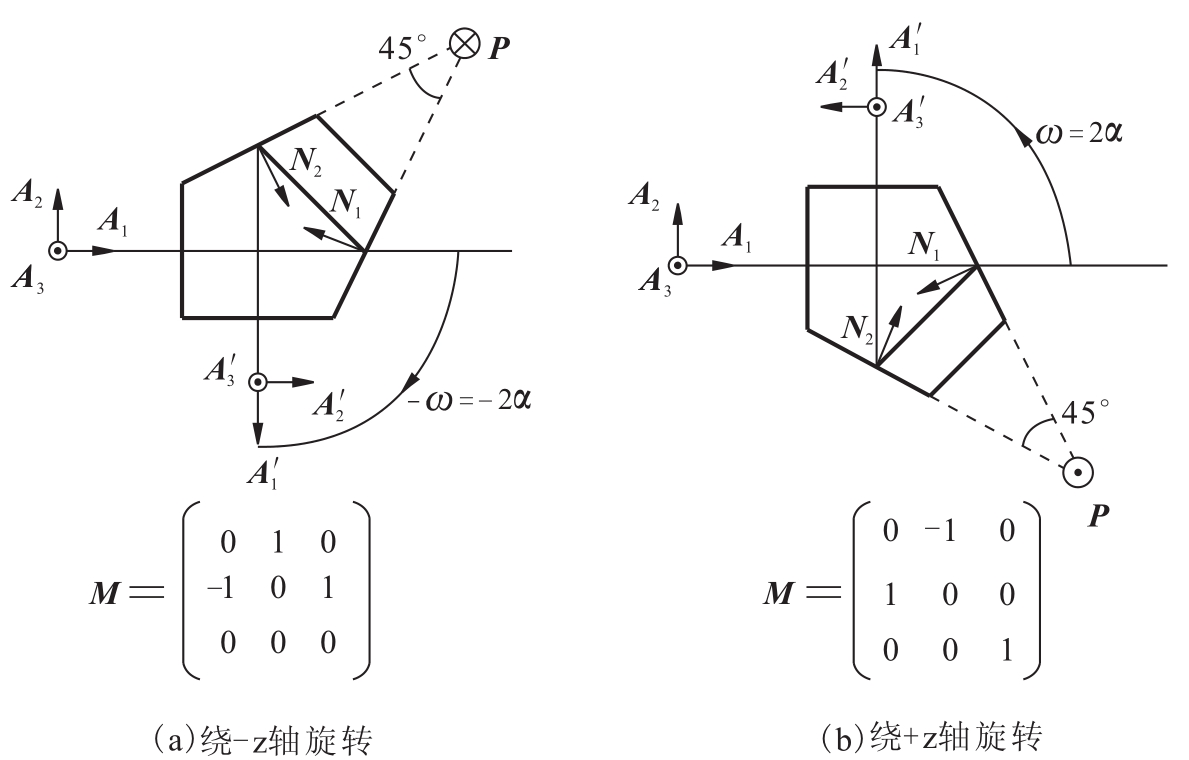
图5.51　两种不同情况下五棱镜的作用矩阵

角镜的作用矩阵表达式（5.85）很重要，这不仅是因为各种类型的角镜应用广泛，而且还因为有些平面反射系统可以简化为等效的角镜。

2）根据标准正交基的成像变换结果求系统作用矩阵

这种方法可以简单迅速地求取平面反射系统的作用矩阵，因而很有实用价值。

在平面反射系统物像关系表达式（5.77）中，若物矢量A（即A₁、A₂、A₃）形式地以标准正交基（i、j、k）取代，根据线性代数中有关线性变换在一组基下的矩阵的理论，正交变换m由它在（i、j、k）处的作用唯一决定，变换后基的像mi、mj、mk（即A₁＇、A₂＇、A₃＇）可以表为基的线性组合，即

借助于矩阵乘法的法则，可以将上式形式地写为

将上式两端同作转置，则有

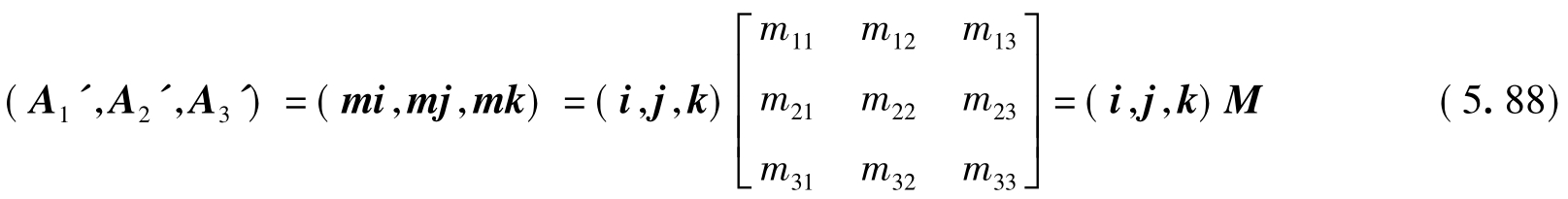
由于标准正交基（i，j，k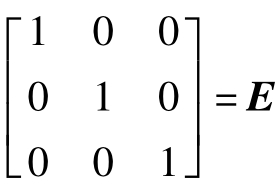）=，即为单位阵，根据矩阵乘法规则，可以得到

M=（mi，mj，mk）=（A₁＇，A₂＇，A₃＇）　　　　　　（5.89）

上式表明，平面反射系统的作用矩阵M可以由标准坐标系o－xyz中，标准正交基的i，j，k经系统所成的像A₁＇，A₂＇，A₃＇决定。作用矩阵M的第一列三个元素就是第一个像矢量A₁＇在o－xyz中的三个坐标（即方向余弦），其余依此类推。作用矩阵M的三列元素分别为A₁＇，A₂＇，A₃＇在标准坐标系o－xyz中的三组方向余弦，表为

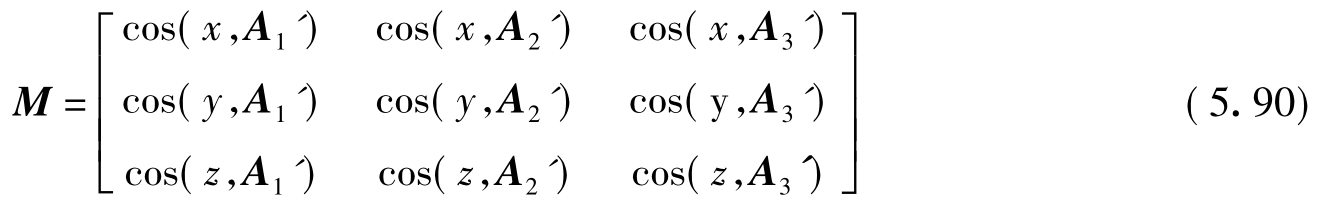
另外，应该指出的是，上面推导过程中采用的形式写法只是一种约定，并非真正的矩阵的乘法。这种形式写法符合矩阵乘法的结合律和分配律，它有利于公式推导的简化。

下面，举例说明利用（5.89）式和（5.90）式求取平面反射系统（反射棱镜）作用矩阵的方法（见图5.52）。再次指出，取图中各反射棱镜的物坐标A₁，A₂，A₃分别与标准坐标系的x、y、z轴方向重合一致。其中A₁沿入射光轴方向；A₃垂直于图平面指向读者；A₂在图平面内并与A₁、A₃构成右手直角坐标系。

［例5.5］　求取下面几种典型棱镜的作用矩阵：

（1）道威棱镜DⅠ－0°（图（a））

（2）五棱镜WⅡ－90°（图（b））

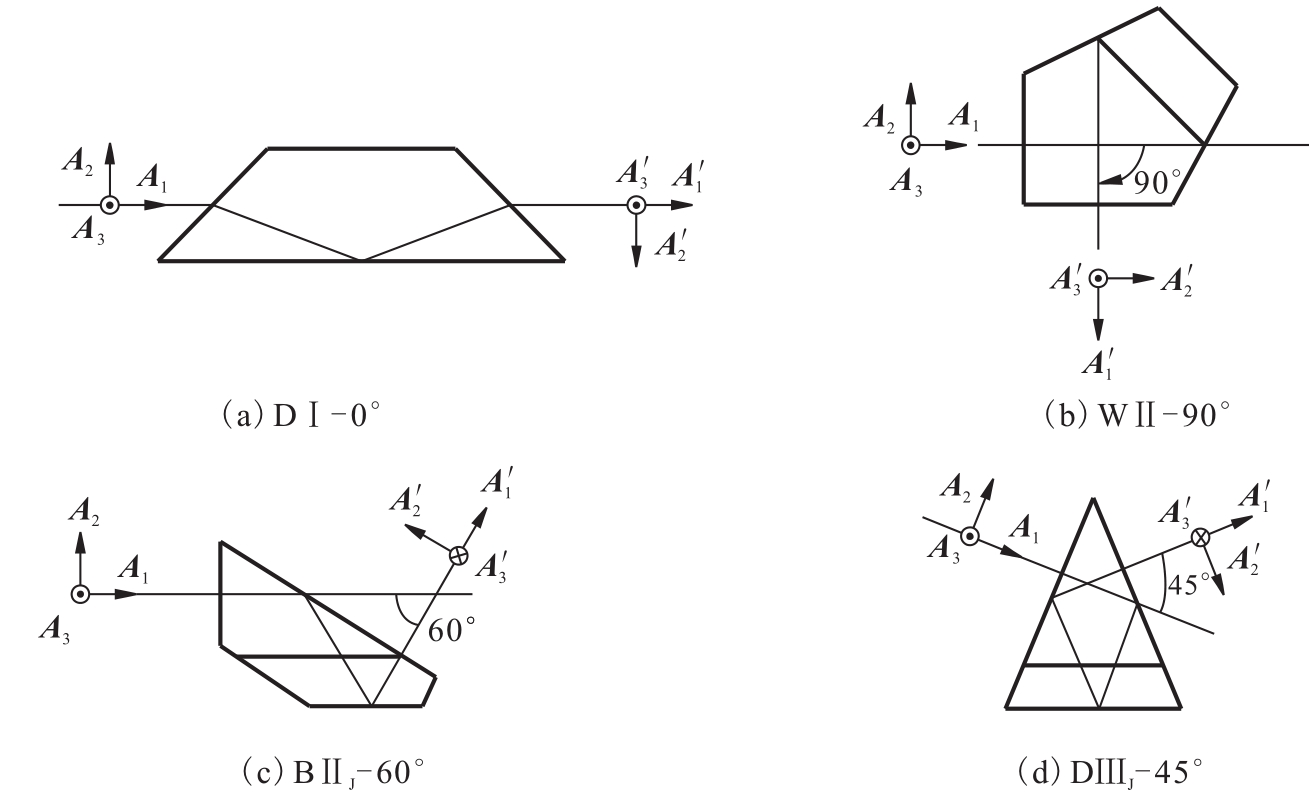
图5.52　几种典型棱镜的作用矩阵

（3）屋脊半五棱镜BⅡJ－60°（图（c））

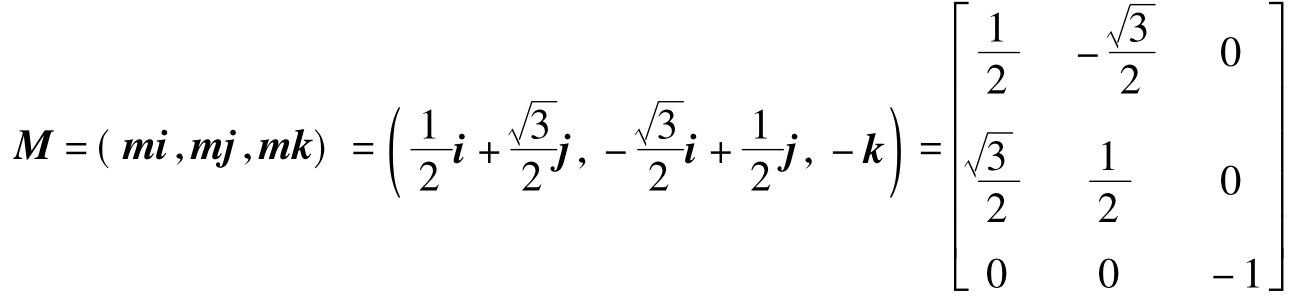
（4）斯密特屋脊棱镜DⅢJ－45°（图（d））

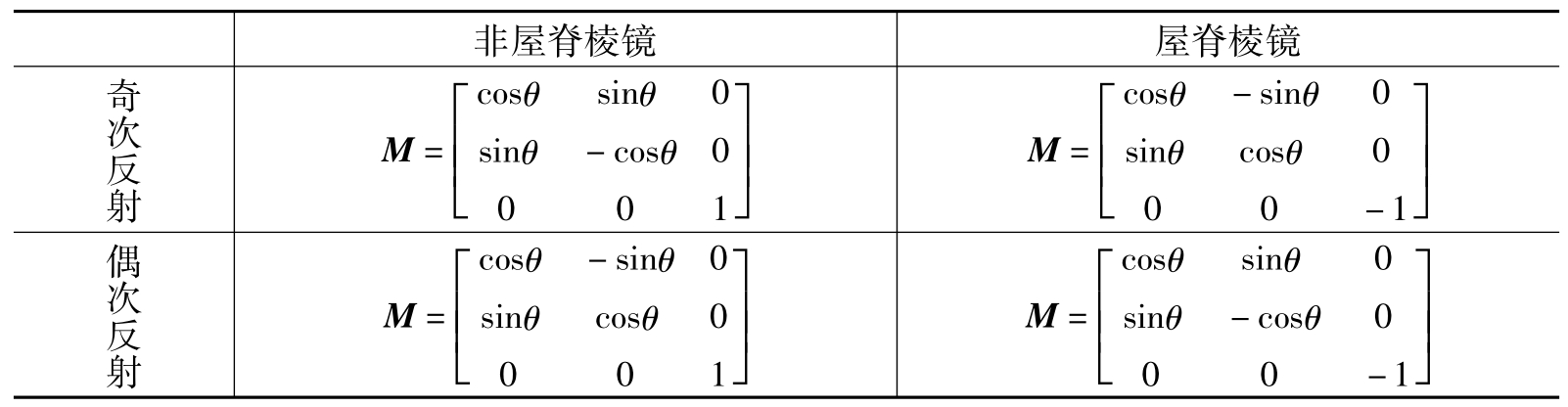
由式（5.90）和上述例子可以看出，对平面反射棱镜作用矩阵M中的各元素取值与光轴折转角度θ、反射次数的奇偶（镜像或一致像）以及有无屋脊面有关，其基本规律可以概括如表5.4所示。

上述讨论解决了平面反射（反射棱镜）系统作用矩阵的求取方法。这样，若给定物空间的坐标矢量，即可方便地求取像空间的坐标矢量。

还应指出，以上所讨论的，是在初始静止情况下平面反射系统（棱镜）对物像的正交变换作用及其作用矩阵；当平面反射系统（以下简称棱镜）由于工作原理的需要或位置误差而产生转动或微量偏转时，物像之间的变换不仅要考虑棱镜本身的变换作用（作用矩阵M），而且还要考虑棱镜转动的影响，为此，尚需研究坐标变换及坐标变换矩阵。限于篇幅这部分内容从略。

表5.4　反射棱镜作用矩阵的计算