单自由度系统的传递函数和频响分析

一个线性非时变单自由度系统振动时的运动方程可写为式（2-51）称为单自由度系统的位移传递函数，该函数描述了在复数s域内单自由度系统的位移响应与激振力之间的映射关系。由拉普拉斯变换性质可得，单自由度系统初态为静止时，其速度和加速度传递函数分别为

式（2-45）还可写成

对以上方程两边进行拉普拉斯变换，得

其中，位移x（t）和f（t）的拉普拉斯变换分别为

式（2-47）可改写成以下形式：

其中

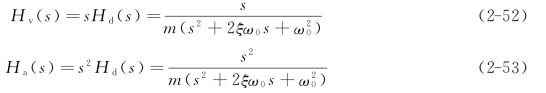
若对式（2-46）两边进行傅里叶变换，可得

其中，位移x（t）和力f（t）的傅里叶变换分别为

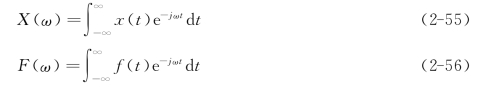
式中，j——单位虚数，即。

式（2-54）可改写为

其中

式（2-58）称为单自由度系统的位移频响函数，该函数描述了在频域ω内单自由度系统的位移响应与激振力之间的映射关系。由于傅里叶变换是拉普拉斯变换在s＝jω的特例，单自由度系统初态为静止时，其速度和加速度频响函数可分别表示为

由于频响函数是复函数，可表达为幅值和相位的形式。以位移频响函数Hd（ω）为例，式（2-58）可写为

其中，幅值和相位的表达式分别为

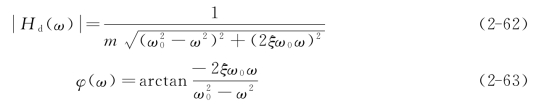
式（2-62）和式（2-63）所表达的单自由度系统位移频响函数的幅频特性和相频特性曲线如图2-1所示。

图2-1　单自由度系统位移频响函数的幅频与相频曲线

得

由式（2-65）解得

为求幅频曲线峰值所对应的圆频率ω′0，可通过求极值的方法来实现，令

由于一般工程结构的阻尼比都比较小（ξ0.1），则可认为

由此可见，幅频特性曲线峰值对应的频率可以确定为系统的固有圆频率。从图2-1的相频特性曲线中，结合相位的表达式（2-63）可以看出，在ω＝ω0处，φ（ω0）＝-90°。可见，相频特性曲线在-90°处对应的频率也可确定为系统的固有圆频率。

为确定系统的阻尼比，可通过半功率点处所对应的频率来求出。在半功率点处，频响函数的幅值可表示为

解方程式（2-68），可得到两个近似解：

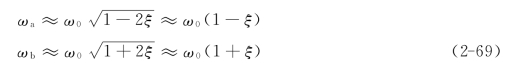
则

可以证明，a，b两频率点在相频特性曲线所对应的相位分别为

于是，可由幅频特性曲线在半功率点处以及相频特性曲线在-45°和-135°处所对应的频率ωa和ωb，按式（2-70）确定系统的阻尼比ξ。

同样，以位移频响函数Hd（ω）为例，式（2-58）可表达成实部和虚部的形式，即

其中，实部和虚部表达式分别为

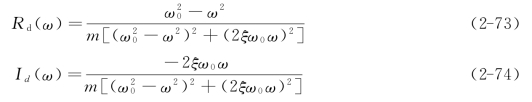
式（2-73）和（2-74）所表达的单自由度系统位移频响函数的实频特性与虚频特性曲线如图2-2所示。从图2-2中可以看出，实频曲线与频率轴的交点处即零值和虚频特性曲线的峰值所对应的频率均为系统固有圆频率ω0。同样可以证明，实频曲线的正负峰值对应的频率和虚频特性曲线峰值的1/2处对应的频率，为半功率点频率ωa和ωb。由此可按式（2-70）确定系统的阻尼比ξ。

图2-2　单自由度系统位移频响函数的实频与虚频曲线

对于单自由度系统的频响分析，也可以直接应用于模态耦合不大的多自由度系统。但是，对于多自由度系统来说，由于实频特性曲线与频率轴的交点以及相频特性曲线与-90°交接处在邻近模态的影响，容易产生水平移动。因此，用幅值的峰值或虚部的峰值所对应的频率作为系统的固有频率较为可靠［26］。

在实际结构中，大多数结构均呈现多自由度的特征，但基本原理与单自由度振动系统是相同的。限于篇幅，在此不多加介绍，可参看振动理论方面的有关书籍。