马柯维茨的均值方差模型

第三节　马柯维茨的均值方差模型

一、模型概述

投资者将一笔资金在给定时期(持有期)里进行投资，在期初，他购买一些证券，然后在期末全部卖出，那么在期初他将决定购买哪些证券，资金在这些证券上如何分配。投资者的选择应该实现两个相互制约的目标——预期收益率最大化和收益率不确定性(风险)的最小化之间的某种平衡。

马柯维茨模型的假设是:

假设一:投资者以期望收益率(亦称收益率均值)来衡量未来实际收益率的总体水平，以收益率的方差(或标准差)来衡量收益率的不确定性(风险)，因而投资者在决策中只关心投资的期望收益率和方差。

假设二:投资者是不知足的和厌恶风险的，即投资者总是希望期望收益率越高越好，而方差越小越好。

马柯维茨均值方差模型就是在上述两个假设下导出投资者只在有效边界上选择证券组合，并提供确定有效边界的技术路径的一个数理模型。

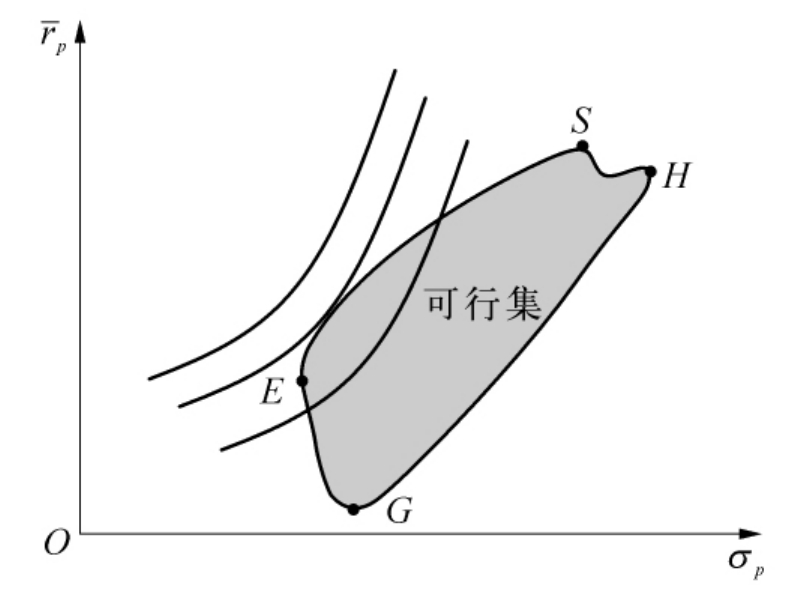
图10－1　可行与有效集

二、有效边界

在马柯维茨均值方差模型中，每一种证券或证券组合可由均值方差坐标系中的点来表示，那么所有存在的证券和合法的证券组合在平面上构成一个区域，这个区域被称为可行区域。

可行域的左边界的顶部称为有效边界，有效边界上的点所对应的证券组合称为有效组合。

三、选择最佳的证券组合

(一)无差异曲线

对一个特定的投资者而言，任意给定一个证券组合，根据他对期望收益率和风险的偏好态度，按照期望收益率对风险补偿的要求，可以得到一系列满意程度相同的(无差异)证券组合。所有这些组合在均值方差(或标准差)坐标系中形成一条曲线，这条曲线就称为该投资者的一条无差异曲线。

同一条无差异曲线上的组合满意程度相同;无差异曲线位置越高，该曲线上的组合的满意程度越高。无差异曲线满足下列特征:

(1)无差异曲线向右上方倾斜;

(2)无差异曲线随着风险水平增加越来越陡;

(3)无差异曲线之间互不相交。

(二)最优证券组合

有效边界上位于最靠上的无差异曲线上的证券组合便是所有有效组合中该投资者认为最满意的组合，即在该投资者看来最优的组合，这一组合事实上就是无差异曲线族与有效边界相切的切点所对应的组合。

如图10－2，投资者选择位于最西北的无差异曲线上的组合。这个组合对应于无差异曲线与有效集的切点。在图10－2中所看到的这一组合是无差异曲线I₂上的O^*。虽然投资者偏好I₃上的组合，然而可行组合中不存在这样的组合。想要位于这条无差异曲线只能是一种奢望而已!至于I₁上，有很多组合可以选择(例如O)，然而，图中显示O^*位于组合O之上，因为O^*位于更西北的无差异曲线上。

图10－2　选择最优组合

四、马柯维茨均值方差模型的应用

(一)估计各单个证券的期望收益率、方差，以及每一对证券之间的协方差或相关系数

假设某证券A在未来给定时期的收益率(记作r)的各种可能取值状况及其可能性(记作p)如下表示:

收益率(r):r₁ r₂…r_n

概率(p):p₁ p₂…p_n

那么证券A在该时期的期望收益率就是未来可能取值的加权平均，其中权数是相应的可能性(概率)。期望收益率记作E_A，即

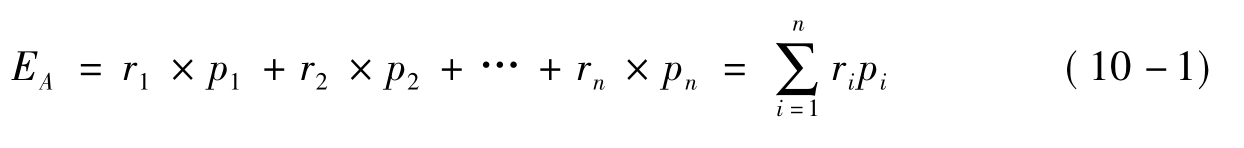
一对证券(A，B)在未来给定时期的收益率的各种可能取值状况为r_i，s_i及其可能性(概率)为p_ij(i= 1，2，…，n; j= 1，2，…，m)，

则证券A与B的协方差为

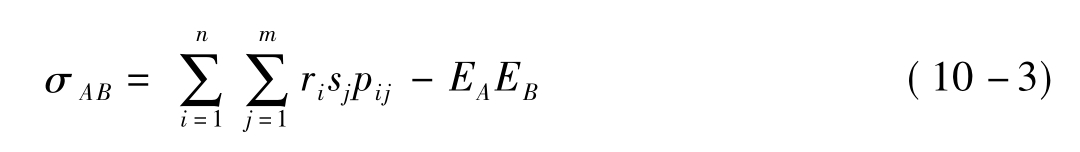
证券A与B的相关系数为

(二)对给定的期望收益率水平计算最小方差组合

假定市场上有证券1，2，…，N，

投资者的投资组合为:投资于证券i的比例为X_i(i= 1，2，…，N)。

则X₁+ X₂+…+ X_N= 1

该投资组合的期望收益率为r_p= X₁ E₁+ X₂ E₂+…+ X_N E_N(10－5)

所有可能的(r_p，σ_p)就构成了(r_p，σ_p)平面上可行区域，对于给定的(r_p)，由下面模型求出组合的最小方差(σ_p)及其对应的组合。

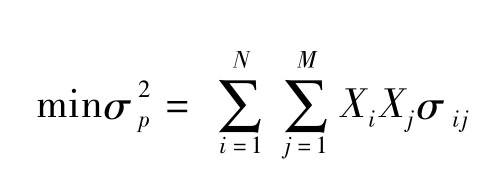
s.t.X₁+ X₂+…+ X_N= 1

X₁ E₁+ X₂ E₂+…+ X_N E_N= r_p

(若不允许买空，则还应满足X_i≥0(i= 1，2，…，N))

取遍可能的r_p，就得到有效边界σ_p=σ(r_p)。　　(10－7)

(三)对于给定的无差异曲线族E= f(σ)，求出最优证券组合

求最优证券组合即求无差异曲线族E= f(σ)与有效边界σ_p=σ(r_p)相切的切点所对应的组合。

五、市场模型

(一)系统风险与非系统风险

单个证券的风险可以分为系统风险和非系统风险两部分。当股市大盘上涨时，大部分股票的价格也上涨;当股市大盘下跌时，大部分股票的价格也随之下跌。这表明市场上存在着一些影响所有证券的共同因素。对个股来说，有时候并不跟随其他股票的波动而同向波动，或者虽然波动但是波幅的大小却很不一致。这主要是由个股自身的因素引起的。对于由共同因素引起股票指数波动而带来的个股价格变化引发的个股收益率的不确定性，叫做系统风险。对于纯粹由个股自身因素引起的个股价格波动带来的个股收益率不确定性，则称为非系统风险。系统风险又叫做不可分散风险，非系统风险又称做可分散风险。

(二)市场模型

1963年夏普提出了市场模型，用以衡量系统风险。该模型假设某种个别证券在给定时期内的收益率与同一时期内的市场指数存在某种线性关系，即

R_i=α_iI+β_iI+ε_i(10－8)

其中，R_i和R_I分别是第i种证券和市场指数的收益率，α_iI、β_iI和ε_i分别是截距、斜率和随机误差项。

需要指出的是:(1)通过截距项的调整，可以使得随机误差项的期望值为0;(2)斜率项常被称为贝塔值，并且β_iI= Cov(R_i，R_I)/V_I，其中，Cov(R_i，R_I)是第i种证券收益率和市场指数收益率之间的协方差，V_I是市场指数收益率的方差。

如果一种证券的贝塔值大于1，我们称之为进攻型证券，它将比市场指数更易变;如果一种证券的贝塔值小于1，我们称之为防御型证券，它的易变性比市场指数小。

图10－3　收益率与市场指数之间的线性关系

六、分散化原理

根据市场模型，任何证券i的总风险都是用它的方差来测度，记为σ²_i，它由两部分组成:(1)市场(或系统)风险，以及(2)个别(或非系统)风险。即

(一)组合的总风险

当一个组合的没一个风险证券的回报率通过市场模型同市场指数的回报率相联系时，那么，对于这个组合的总风险，情况如何呢:如果对于给定的组合P，投资于每一证券i的资金比例记为X_i，则组合的回报率为

将方程中的r_i用方程r_i=α_iI+β_iI r_I+ε_iI的右边代替，将导出组合的市场模型:

其中:

方程(1)和(2)中，表明组合的截距α_pI和贝塔值β_pI分别为各证券的截距和贝塔值的加权平均，使用它们的相对比例作为权数。同样，在方程(3)中，组合的随机误差项ε_pI是各证券的随机误差项的加权平均，还是以相对比例为权数。于是组合的市场模型是方程r_i=α_iI+β_iI r_I+ε_iI所给出的单个证券的市场模型的直接扩展。

从方程α_pI+β_pI r_I+ε_pI可知，由组合回报率的方差测度的组合的总风险，记为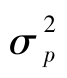将等于:

其中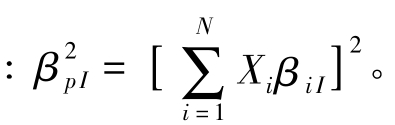

假设各证券的随机误差项之间是不相关的:

(二)组合的市场风险

一般地，一个组合越是分散化(即，组合中包含的证券数越多)，每一个证券的比例X_i越小。这将不会引起β_pI显著减小或增大，除非刻意在组合中增加相对低的或高的贝塔值的证券。也就是说，因为一个组合的贝塔值是其证券的贝塔值的加权平均，没有理由认为增加分散性，会引起组合的贝塔值，继而是组合的市场风险向一特定方向发生变化。因而，可以得出结论:分散化导致市场风险的平均化。这个结论是合理的，所以当经济前景转向萧条(或繁荣)时，大多数证券的价格将下跌(或上升)。不管分散化程度如何，组合的回报率总是对市场普遍性影响很敏感的。

(三)组合的个别风险

对于个别风险，情况是完全不同的。在一个组合中，一些证券因为其发行公司意料之外的好消息而上涨。其他一些证券则因为公司未预料的坏消息而下跌。总的来看，预期有好消息和坏消息的公司数量近似相同，这导致一个好的组合的预期的净影响很小。即当组合变得更加分散时，个别风险，进而总风险将变得更小。

方程的方括号中的值正是各个证券的个别风险的平均值，但组合的个别风险只有这个值的1/N。现在，当一个组合变得更加分散时，证券数N变得更大，从而1/N变得更小，导致组合更小的个别风险。即:分散化可以减小个别风险。

粗略地说，一个包含30种或更多的随机选出的证券的组合将有一个相对很小的个别风险。即它的总风险略微大于其市场风险。从而这个组合是一个“好的组合”。如图10－4描述了分散化如何导致个别风险的减少和市场风险的平均化。

图10－4　风险与分散化