函数零点与方程根的讨论

§3.4　函数零点·方程根的讨论

相关知识点和工具：罗尔中值定理；闭区间上连续函数的零点存在定理；函数单调性；罗尔定理的推广：设f为n阶可导，且有n＋1个零点，则f^（n）（x）至少有一个零点。但此结果不能逆推！！

例1　证明方程2^x－x²－1＝0恰有三个不同实根。

证　首先证有三个不同实根，不妨结合几何图形分析根的大概位置。

x₁＝0，x₂＝1，x₃介于4和5之间。再证仅此三根。

反证法，若有第四个根，则f（x）＝2^x－x²－1的三阶导数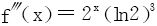应有至少一个零点，矛盾。

注　最好不要用图形代替证明，即严密化证题。

例2　已知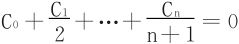，则方程C₀＋C₁x＋…＋C_nxⁿ＝0在（0，1）内有根。

分析　设根为ξ，则C₀＋C₁ξ＋…＋C_nξⁿ＝0，联系Rolle定理，构造一个函数f（x），st　f′（ξ）＝C₀＋C₁ξ＋…＋C_nξⁿ即可。

例3　设f∈［a，b］，且当0≤k≤n时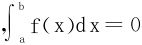，，求证f（x）在［a，b］上至少有n＋1个零点。

分析　从n＝1情形入手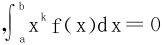说明f（x）至少有一个零点x₀且f（x）要变号。若f（x）仅有x₀唯一的零点，则f在［a，x₀）和（x₀，b］上符号相反。又若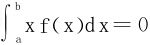，则必有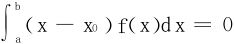，由于f在x₀的两侧只变号一次，则（x－x₀）f（x）在［a，x₀）∪（x₀，b］上恒正或恒负，矛盾。

证明　反证法。若不然，f在［a，b］上只有m（m≤n）个零点：

a≤c₁<c₂<…<c_m≤b，令P_m（x）＝±（x－c₁）（x－c₂）…（x－c_m），选取＋、－号使P_m（x）与f（x）在［a，b］上同号即可得。

例4　若f（x）在R上可导，且f（x）＋f′（x）>0，试证f（x）至多只有一个零点。

分析　条件f（x）＋f′（x）>0不易应用，联想本讲义§1.3之例2。作辅助函数F（x）＝e^xf（x）则有F′（x）＝e^x（f（x）＋f′（x））。

证一　引入F（x）＝e^xf（x）从条件知F′（x）>0，于是F（x）是R上严格递增函数。则F（x）至多有一个零点，而e^x>0，故f（x）至多只有一个零点。

证二　反证法。若f（x）有两个零点，x₁，x₂，则F（x₁）＝F（x₂）＝0，由Rolle定理，∃ξ∈（x₁，x₂），st　F′（ξ）＝e^ξ（f（ξ）＋f′（ξ）＝0，但e^ξ>0，故f（ξ）＋f′（ξ）＝0，矛盾。

注　反证法其实证明了原命题的逆否命题，在f（x）的两个零点之间，一定有f（x）＋f′（x）的零点。

派生题1：设f在［a，b］上连续，在（a，b）内可导，且f（a）＝f（b）＝0，求证：

∀实数λ，∃c∈（a，b），st　f′（c）＝λf（c）。

关键：构造辅助函数F（x）＝e^－λxf（x）。

派生题2：设f，g∈C^*［a，b］，f（a）＝f（b）＝0，试证∃ξ∈（a，b），st

f′（ξ）＋f（ξ）g′（ξ）＝0

关键：引入F（x）＝f（x）e^g（x），F′（x）＝e^g（x）（f′（x）＋f（x）g′（x））

思考：在同样的条件下，证明存在一个η使得f′（η）＋f（η）g（η）＝0

置换思路，此处g（η）相当于题目中的g′（ξ），构造。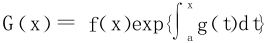

例5　设f（x）∈C［a，b］，且∀x∈［a，b］，有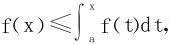试证f（x）≤0。

分析　反证法，若∃x₀∈［a，b］，st　f（x₀）>0，存在邻域U（x₀，δ）在其上f（x）>0似乎推不出矛盾。

证明　令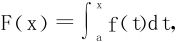则原条件变为F′（x）－F（x）≤0，再引入辅助函数G（x）＝e^－xF（x），G′（x）＝e^－x（F′（x）－F（x））≤0，于是G（x）是递减函数，∀a<x≤b，G（x）≤G（a）＝e^－aF（a）＝0⇒F（x）≤0，由原条件f（x）≤F（x），立知f（x）≤0。

注　凡f′（x）＋λf（x）类型的项一般联想到e^λxf（x）的导数。

例6　证明方程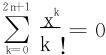有且仅有一个实根。

证一　为简便，引入记号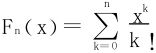！，由于F_2n＋1（＋∞）＝＋∞，F_2n＋1（－∞）＝－∞，故F_2n＋1（x）＝0显然有解。

设ξ是F_2n（x）的最小值点，则ξ一定是其极小值点，于是F′_2n（ξ）＝0，即F_2n－1（ξ）＝0，。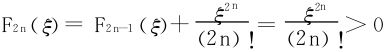

严格的书写可以采用归纳法。

F₁（x）＝0有唯一的零点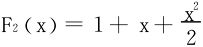，，由于判别式Δ<0，故无零点。且F₂（x）>0，于是F₃（x）有唯一的零点，…

证二　令G（x）＝e^－xF_2n＋1（x），易推得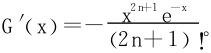

当x>0时，G′（x）<0，G（x）单调递减，且由F（0）＝1，F（＋∞）＝0知G（x）在（0，＋∞）上没有根。当x<0时，G′（x）>0，G（x）单调递增，且F（－∞）＝－∞，故有唯一的根。但e^－x恒正，于是F_2n＋1（x）有唯一的根。

例7　证明xⁿ＋x＝1在（0，1）上存在唯一的根x_n，并且x_n→1，（n→∞）。

分析　从几何图形转化为两曲线y＝xⁿ和y＝1－x相交的问题。

令F_n（x）＝xⁿ＋x－1。从F′_n（x）>0易推知根的存在唯一性。下证。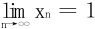

证明　首先证｛x_n｝↗，F_n（x_n）＝F_n＋1（x_n＋1）＝0

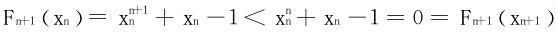，且F_n＋1（x）递增。故有x_n<x_n＋1；又0<x_n<1，推出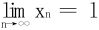存在。

其次证明l＝1。反证法，若不然，设l<1，∃ε₀，st　l＋ε₀<1，∃N，当n>N时x_n<l＋ε₀<1，所以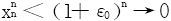。由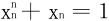，令n→∞又应当有l＝1，得出矛盾。

例8　设f在R上二阶可导且f″（x）>0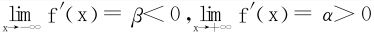，，且∃x₀，st　f（x₀）<0，求证f（x）在R上有且仅有两个零点。

分析　f″（x）>0⇒f′（x）↗，结合条件∃c，st　f′（c）＝0。

在（－∞，c）上，f′（x）<0，f（x）↘，在（c，＋∞）上，f′（x）>0，f（x）↗，故f（c）必是f的最小值点，且f（c）<0。然后证当｜x｜充分大时，f（x）>0即可。

例9　设f（x）在［0，1］可微，∀x∈［0，1］，0<f（x）<1，且f′（x）≠1。试证存在唯一的ξ∈（0，1），st　f（ξ）＝ξ，亦即f（x）存在不动点。

证明　引入F（x）＝f（x）－x，F（0）>0，F（1）<0，且F（x）连续，推出∃ξ，st　F（ξ）＝0。下证唯一性。

若不然，还存在另一个η，使得f（η）＝η，不妨设0<ξ<η<1，在区间［ξ，η］上用Lagrange中值定理，∃x₀∈（ξ，η），st　f（η）－f（ξ）＝f′（x₀）（η－ξ）。

所以f′（x₀）＝1，与题设矛盾。

或用f′（x₀）≠1⇒F′（x）≠0，且F（1）<F（0）知，F（x）必为严格递减。故其零点唯一。

例10设f（x）＝a₀＋a₁cosx＋…＋a_ncosnx，其中a_i∈R，且

a_n>｜a₀｜＋｜a₁｜＋…＋｜a_n－1｜

证明：f^（n）（x）在［0，2π］内至少有n个零点。

分析　鉴于事实“求导一次，零点少一个”，猜测f（x）必至少有2n个零点。而条件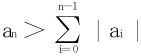表明f（x）的构成项中，末项a_ncosnx是龙头老大，有多少零点它说了算。显然cosnx在［0，2π］中完成了n个周期，故有2n个零点。剩下的是证明f（x）亦有2n个零点。

例11　设u_n（x）＝（x²－1）ⁿ

（2）证明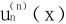的一切根全在（－1，1）之内。

证明　（1）法一：利用Leibniz乘积求导公式u_n（x）＝（x－1）ⁿ（x＋1）ⁿ

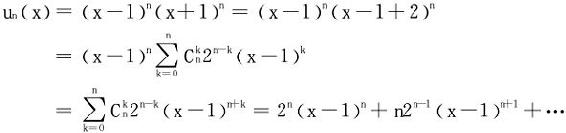
仍推知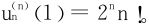

（2）±1是u_n（x）的两个n阶零点，继而是u′_n（x）的n－1阶零点，由Rolle定理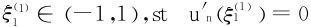，∃。仍由Rolle定理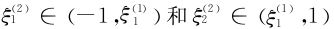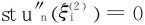，∃（i＝1，2）。且±1是u″_n（x）的n－2阶零点，…反复n次得知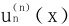不再以±1为零点，而n个零点全位于（－1，1）之内。注意到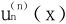是n次多项式，上述n个零点构成其全部零点。

注　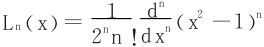即为勒让德多项式。

习题3.4

1．讨论方程4^x－3x³－1＝0的根。

2．给出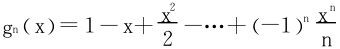，证明当n为奇数时，g_n（x）恰有一个零点；当n为偶数时，g_n（x）无实零点。

3．设在［1，＋∞）上，f″（x）<0，f（1）＝2，f′（1）＝－3，证明f在［1，∞）上仅有一个零点。

4．设f（x）在R上二次可微，且有界，试证f″（x）有零点。

5．若f在R可导，且∃0<λ<1，st｜f′（x）｜≤λ，证明f（x）存在不动点。

6．设f∈C^*［a，＋∞），且f（a）<0，证明：若∀x>a，f′（x）>c>0，则f（x）在（a，＋∞）内必有唯一的零点。

　又问：条件f′（x）>c>0，削弱为f′（x）>0，结论是否仍然成立？

8．f_n（x）＝x＋x²＋…＋xⁿ，证f_n（x）＝1在［0，∞）上有唯一实根x_n，且limx_m存在，并求其值。

（北师大97）

9．f_n（x）＝sinx＋sin²x＋…＋sinⁿx，证明f_n（x）＝1在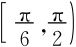内存在唯一解x_n，且。（n→∞）

（北师大99）

10．证明f（x）＝x²ⁿe^－x的n阶导数f^（n）（x）在x>0范围内至少有n个零点。

11.∀a，b，c∈R，证明方程e^x＝ax²＋bx＋c至多有三个根。

（浙江大学2000年）