【摘要】：根据问题的具体情况，选取一个变量例如为积分变量，并确定它的变化区间设想把区间分成个小区间，取其中任一小区间并记为，求出相应于这小区间的部分量的近似值.如果能近似地表示为上的一个连续函数在处的值与的乘积，就把称为量的元素且记作，即； 以所求量的元素为被积表达式，在区间上作定积分，得，即为所求量的积分表达式，这个方法通常叫做元素法。
(1/2) 定积分的元素法的一般步骤
（1）根据问题的具体情况，选取一个变量例如
为积分变量，并确定它的变化区间
（2）设想把区间
分成
个小区间，取其中任一小区间并记为
，求出相应于这小区间的部分量
的近似值.如果
能近似地表示为
上的一个连续函数在
处的值
与
的乘积，就把
称为量
的元素且记作
，即
； （3）以所求量
的元素
为被积表达式，在区间
上作定积分，得
，即为所求量
的积分表达式，这个方法通常叫做元素法。
(2/2) 体积
旋转体的体积： （i）平面图形由曲线
与直线
，
，
轴所围成： 绕
轴旋转一周而成的旋转体的体积为
； 绕
轴旋转一周而成的旋转体的体积为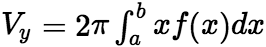
。 （ii）由连续曲线
及直线
，
，
轴所围成的平面图形 绕
轴旋转一周而成的旋转体的体积
； 绕
轴旋转一周而成的旋转体的体积
。
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
