无限个自然数相加

算术一般只能处理数量关系有限的问题，但提供了人类思维的基础与条件. 人类的认识能力是逐步深化的. 甚至是超时空的. 从数学的发展我们至少可以领悟到: ①无限是有限的延伸;②有限由无限组成; ③演绎法是认识无限的有力武器.

1.无限是有限的延伸

自然数列1，2，3，…有始无终，没有尽头，古已有之，自然数集合中的元素的数目显然是无限的了，但自然数有一个特性，就是如果一个数是n的话，他后面的那个数一定是n+1，于是我们可以用1，2，3，…，n，…完整地表达有无限个自然数，但这种认识也只限于普通的归纳阶段.

在数学中，真正从有限进入无限，得到普遍的定理，是通过数学归纳法. 1891年，意大利数学家皮亚诺(G.Peano，1858—1932)在他的《算术原理新方法》一书中，用公理方法给出了自然数理论，建立了一个自然数的公理系统. 它包含三个原始概念(集合、自然数、后继者)和五条公理:

①1是一个自然数;

②1不是任何自然数的后继者;

③每一个自然数a都有一个后继者;

④如果a的后继者与b的后继者相等，那么a与b也相等;

⑤若一个由自然数组成的集合S，1属于S，又若当任一数a属于S时，它一定也有a的后继者属于S，则S就含有全部自然数. 最后这条公理称为归纳公理，它是数学归纳法的逻辑基础。

数学归纳法是建立在归纳公理之上的，它的陈述通常是: 如果一个命题A(n)，当n=1时成立，又假定该命题当n=k时成立，能证明n=k+1时也成立，那么就可以断言，这个命题对于所有的自然数都成立.

初学数学归纳法的人，似乎不大理解，如此这般就可证明有关自然数的命题，觉得与一般经验归纳法并无区别. 其实这是误解，数学归纳法的本质是演绎推理，所证命题必然含于归纳公理之中. 如果一个命题在经验归纳法之下，证实了千百次或者更多，都不能说该命题得到了证明，顶多可算作合理的假设，这也告诉我们，对有关自然数的命题，一个一个地验算是不行的，因为自然数有无限多个，必须采用数学归纳法，这是使有限向无限延伸的科学办法.

太阳光线在人们所处的空间中，被认为是平行的，但它们来自太阳，因而这些平行光线应交于一点(太阳). 这样一个事实，启发了数学家，在处理几何图形时，如果把无穷远元素(无穷远点，无穷远直线，无穷远平面)和非无穷远元素平等看待，不加区别，那么这个几何图形所处的空间就扩大了，这个扩大了的空间称为射影空间. 同样，把加上了无穷远点的直线称为扩大的直线，把有无穷远直线的平面称为扩大的平面，在三维欧氏空间中，一切无穷远点组成的集合称为无穷远平面，加上无穷平面后的空间称为扩大的空间.在射影空间中，平行的概念消失，共面的两条直线或一个平面和一条直线总相交于一点，两个平面总相交于一条直线. 此外，每两点总决定一条直线，每三个不共线的点总决定一个平面，等等.

射影几何的奠基人，法国数学家笛沙格(G.Desargues， 1591—1661)在1636年出版的《试论锥面截一平面所得结果的初稿》中利用无穷远点和无穷远直线，提出了他的假定，又称笛沙格定理: 如果两个三角形ABC和A'B'C'的对应边的交点P、Q、R处于同一直线上，则其对应顶点的连线相交于同一点. 反之，如果三角形ABC和A'B'C'的对应顶点的连线相交于同一点，则其对应边的交点处于同一直线上. 笛沙格指出，如果前者成立，那么后者也成立. 这是两个对偶的命题，是射影几何的一条重要定理. 关于对偶命题，对偶原理成立. 对偶原理是指: 若射影平面空间对偶命题(合理或定理)中的一个是正确的，则另一个命题也是正确的，两个对偶命题只不过手续与内容互换而已.

自然数集合的无限，笛沙格定理无穷远元素的引入都是从有限个自然数或有限元素来的，是从有限中外推得到的，从而导出了数学归纳法和对偶原理. 这是把有限与无限巧妙联系的结果.

2.有限由无限组成

古希腊毕达哥拉斯学派信奉“万物皆数”的信条，而这个数指的整数与分数，后来发现，没有任何有理数与数轴上这样上点相对应(图2.1): 距离OP的长度，它等于边长为1的正方形的对角线长，引起了第一次数学危机.继而，又发现数轴上还存在许多点也不对应于任何有理数，可见数轴上点是非常稠密的，短短一条线段就可以反映出无穷的数. 我国古代庄子有一句名言: “一尺之棰，日取其半，万世不竭.”相比之下，这个认识就高明得多. 如果把图2.1中带箭头的直线看作数轴，把直线的中点作为原点O，在数轴取定单位. O点左边表示负数，右边表示正数，那么这条数轴就可容纳下全部实数，即使取0到1的单位长线段，我们都可以把0到1的所有有理数的点找出来. 这么多的有理点仍不能把这个单位长线段填满. 而无理数不能化为有理数，因此，0到1的单位长线段就留有空隙，它们对应着无理点，于是我们可以断言，在0到1的单位长线段里，仍然包含着无数有理点和无数无理点，表明这样一条有限长的线段是由无限多个点组成的，这样一个事实，数学家直到19世纪才彻底弄清.

图2.1

1874年德国数学家魏尔斯特拉斯(K.T.W.Weierstrass， 1815—1897)给出了一个处处不可微的连续函数的经典例子:

图2.2 科赫曲线

假定原来的等边△ABC，面积为S. 每一边三等分使△ABC分为9个全等的等的等边三角形，设每一个的面积为a，因此，S=9a，a=S/9，即第一次外翻的尖角形面积a≈S/9.

考虑确定雪花曲线六个初始尖角中每一个面积的极限. 大尖角的面积是a，在由它生成下一批尖角中每一个尖角具有面积a/9，相继所生成尖角的面积为，…，注意每一阶段尖角的个数，把这个尖角本身及其不断生成的各个尖角的面积相加，即

把六个尖角中每一个所造成的面积相加，再加上原来生成三角形内部的六边形得到

科赫曲线用无限的周长占了一个很有限的地盘，奇异极了!还有，普通的几何对象具有整数维: 零维的点、一维的线、二维的面、三维的立体，乃至四维的时空. 它们的维数都是整数. 而科赫曲线的维数不是整数，比一维大比二维又小，是1.2618. 科赫曲线以无限的长度挤在有限的面积内，确实占有空间，而这个空间的维数是分数，实在令人寻味.

在有限与无限的认识上，人们存在一个误区，就是认为无限比有限大，比有限多，无限应包含有限，无限由有限组成. 通过上述两个例子，我们看到，人们上述认识不总是正确的，无限地可以寓于有限，有限也可包含无限. 有限与无限的这种联系，是由数学家首先发现和运用的.

3.演绎法建造无限的乐园

集合论的发展是现代数学的巨大成就之一，当今，几乎没有哪一个数学分支不或多或少地受到集合论思想和方法的影响.

集合论初期产生过一些悖论，后来把集合论建立在公理系统的框架内，人们也就觉得安全了.

康托尔采用匹配的方法(也就是一一对应的方法)来研究无限集，他发现，自然数集、整数集、素数集、有理数集等都构成一一对应关系. 并把这些具有一一对应关系的集合称为等势的集合，称它们有相同的基数. 这个“数”是最小的无限数，亦称超限数，记作(读作阿列夫零).它是和所有自然数集有相同大小的一切集合的共性. 康托尔发现，任一线段上的点与全直线上的点，与正方形的内的点，与立方体内的点，构成一一对应，而一条直线上的点与n维空间的点构成一一对应. 但是自然数集与无理数集不等势，有理数集与实数集不等势，n维空间的点与实函数集合不等势. 康托尔证明了，对于每个非空集合，无论它是有限的还是无限的，都存在比它包含的元素更多的集合. 并且一般地任取一个无限集合，总可以利用它作出一个新的集合，这个新的集合具有比前者更大的基数，不能设想这个过程会有尽头，因此，康托尔认为，存在着无限多个不同的超限数，它们可排成一个上升列:，…，其中每一个都比前一个“大”.

有限数与超限数完全不同，表现在如下三个方面.

第一，就部分与全体关系而言，有限数部分小于全体; 超限数部分可以等于全体: 奇数集合与自然数集合一样大，无理数集合等于实数集合，等等.

第二，有限数与超限数运算法则不同，例如

它可解释为非负偶数集合与自然数集合可建立一一对应关系:

0 2 4 6 8 … 2n …

1 2 3 4 5 … n …

表2-1

这个序列包含着有先后次序的全部有理数舍去a与b有公因子的所有，每个有理数就以最简单的形式恰好只出现一次，如此，就使有理数集合与自然数集合构成了一一对应. 而每行的基数是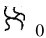，故有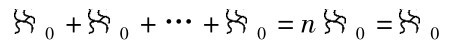

即可数无限是可数的. 还有

这些运算在有限数学中是不存在的.

第三，有限数和超限数与现实关系不同.

一个有限数无论它多大，都可以找到现实背影，以及与现实的联系; 超限数在现实中找不到背景，它既不存在于自然界，也没有为理性思维提供合理基础.

由上所述，无限整体意义上的无限，只能通过想象力和演绎方法才能发现. 超限数的创立纯属演绎思维的产物，它脱离有限而存在，也割断了与现实之间的联系.