实测研究整体思路

第一节　实测研究整体思路

首先，选择具有代表性的服装品牌作为研究对象，根据服装领域的专家对服装市场的综合理解，通过专家访谈收集数据，并运用权重层次分析法和层次分析法辅助软件Yaahp5.0，确定出不同服装类别的权重系数。然后，利用对消费者进行随机抽样调查，运用服装品牌个性量表作为测量工具测得第一手数据，通过分析可得到服装品牌个性在五个维度上的具体表现。

在整个过程中，运用了一个重要的数据处理方法，即层次分析法(Analytical Hierarchy Process，简称AHP)。层次分析法是美国匹兹堡大学运筹学家萨迪(A.L.Saatty)于20世纪70年代提出的，它是一种定性与定量分析相结合的多目标决策分析方法。它特别适合于具有复杂层次结构的多目标决策问题。目前已经在各国得到广泛应用^[1]。

层次分析法^[2]的基本思想是:通过分析复杂问题包含的各种因素及其相互关系，将问题所研究的全部元素按不同的层次进行分类，标出上一层与下一层元素之间的联系，形成一个多层次结构。在每一层次，均按某一准则对该层元素进行相对重要性判断，构造判断矩阵，并通过解矩阵特征值问题，确定元素的排序权重，最后再进一步计算出各层次元素对总目标的组合权重，为决策问题提供数量化的决策依据。

层次分析法的步骤是:

(1)对实际问题进行分析，构造一个层次结构模型(评价指标层次体系)，包括指标层、准则层和措施层。

(2)逐层进行成对比较，得到若干正逆对称矩阵，即判断矩阵。为了使各因素之间进行的两两比较能够得到量化的判断矩阵，引进九分等级制，见表5-1。

表5-1　九分等级制

(3)计算判断矩阵J的最大特征值λ_max和其对应的特征向量W=(W₁，W₂，…，W_n)，特征向量W即为评价指标的权重向量。引入方根简化算法求特征值和特征向量，具体步骤如下:

①计算判断矩阵每行所有元素的几何平均值

得到=(，，…，)。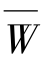

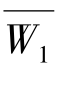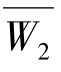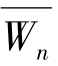②将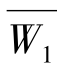归一化，即计算

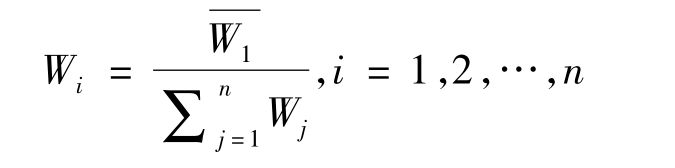
得到W=(W₁，W₂，…，W_n)，即为所求特征向量的近似值，这也是各评价指标的相对权重。

③计算判断矩阵的最大特征值λ_max

其中(W_j)_i，为向量Wj的第i个元素。

(4)为了减少由专家打分对权重向量计算产生的随机性因素，必须对判断矩阵进行一致性检验。一致性检验性的步骤如下:

①计算一致性指标CI，CI=(λ_max- n)/(n-1)，n为判断矩阵的阶数。

②选择随机一致性指标RI，对于1～9阶矩阵，一致性指标见表5-2。

表5-2　一致性指标

③计算CR，CR=CI/RI，若CR＜0.10时，判断矩阵有满意的一致性，否则就要对判断矩阵进行调整。

(5)当所有的判断矩阵都满足一致性条件时，最后根据复合原理求出组合权系数。