假设在一个总体中只含有下面20个个体:
12,11,8,11,9,10,11,10,8,10,
8,11,9,10,13,8,11,9,12,13,
从该总体中任意抽取5个个体得到样本1:9,10,12,10,11;算出平均数为10.4,把它写在一张小纸条上,放入一个口袋中,然后将这5个数放回总体.再从总体中随机抽取5个,得到样本2:10,11,9,8,13;将其平均数10.2写在小纸条上放入袋中,将抽得的5个数放回总体.依次重复500次,在口袋中就会有500个平均数,作出这些平均数的频率直方图,如图5.1所示.

图5.1 500个样本均值的直方图
这件事如用手工进行操作有点麻烦,好在这些计算和作图,都可在计算机上非常方便地利用统计软件来实现.
如果将图5.1中的各个小矩形顶端的中点用一条折线连接起来,就会呈现出“中间高,两边低,左右基本对称”的形状.可以想象,如果我们不断增加平均数的个数,并且使分组增多,分组的区间不断细分,那么频率直方图的对称性就越来越好,最后频率直方图上的折线就越来越接近图5.2中所画出的曲线.这条漂亮的曲线就是非常著名的正态分布曲线,可简称为正态分布.

图5.2 正态分布曲线
如果随机变量ξ的密度函数(参阅附录1)为
![]()
则称ξ服从正态分布N(μ,σ2),简称为ξ~N(μ,σ2).
公式(5.1)中的σ是正态分布的标准差,μ是正态分布的平均值,л是圆周率的常数3.14159,e是常数2.71828.正态曲线与x轴之间的面积为一个单位面积.
正态分布曲线在平面直角坐标系内的图形如图5.3所示,它具有如下性质:
(1)曲线是一个对称图形,对称轴是直线x=μ.整个图形像一口钟,因此正态分布曲线又称为钟形曲线.

图5.3 正态分布曲线在平面直角坐标系内的图形
(2)在x=μ处曲线有最高点.当x自μ分别向左、右远离时,曲线不断降低,呈现“中间高,两边低”的形状.
(3)曲线以x轴为渐近线,无论向左或向右延伸,都越来越接近x轴,但是永远不会与x轴相交.
(4)曲线的形状依赖于两个参数μ和σ.参数μ的变化表示曲线的左右平移,但是不改变曲线形状.参数σ的变化引起曲线形状的改变,σ大则曲线矮胖,σ小则曲线高瘦.为了确定一个具体的正态分布,只需要知道两个参数值:平均值μ和标准差σ.
图5.4显示的3种正态分布,每种都有相同的平均数,但是各有一个不同的标准差.这些曲线具有不同的形状,当σ=10时,曲线最矮胖;当σ=1时,曲线最高瘦;当σ=5时则居中,不胖不瘦.但是,它们都具有相同的对称轴:直线μ=50.

图5.4 平均数相同但标准差不同的正态分布
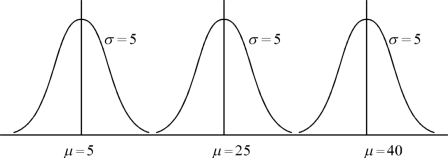
图5.5 平均数不同但标准差相同的正态分布
图5.5说明一族正态曲线,它们的标准差相同,但是各有一个不同的平均数.这些曲线的形状完全相同,所不同的只是位置,相互之间可经过左右平移得到.
图5.6显示3个不同的正态分布,每种都有一个不同的平均数和一个不同的标准差,因此,3种正态曲线的形状和位置都不相同.

图5.6 平均数和标准差都不同的3个正态分布
正态分布是由法国数学家德·隶莫佛(A.de Moivre,1667—1754)于1733年引进的,当时他用它作为二项随机变量当参数n较大时的近似概率.后来,拉普拉斯和其他一些数学家推广了这个结果,这些现在已包含在著名的中心极限定理中.
大约从1800年以来,科学家对正态曲线已经相当熟悉了,因为它经常出现在有关的测量中.假设一位科学家对某金属棒的精确长度感兴趣.他知道,由于人的手和眼睛不是非常的准确,测量仪器会有一定的误差,周围环境例如温度也会对测量结果产生影响.因此,他在测量长度时不是只测量一次两次,而是要测量很多次,例如50次.如果根据这50次测量值绘制成频率直方图,这个图形会趋近一条正态曲线.测量次数越多,它们的频率分布就会越接近正态曲线.
这是因为,在认真进行的一组测量中,误差应该归结为手和眼造成的误差,以及所用测量仪器的随机变化.所有这些误差都应该分布在准确值的两边,并且紧紧地围绕这个值.这如同一个神枪手对准目标射击时,他射出的子弹落在目标上的枪眼就应当聚集在一起,而且与中心的距离呈现越来越小的趋势.
测量的正态曲线对科学家非常有用.在正态分布中,数据围绕着平均值,也就是趋近准确值.因此,如果大规模测量遵循正态分布,就可用大量测量的平均值作为测量准确值的最佳逼近.而且,如果大规模的测量呈现非正态分布,那么就说明已经有某些附加的影响渗透到测量中去了,应该找出这些因素并加以清除.例如,在一间温度不断升高的屋子里测量金属棒的长度,因为金属棒受热膨胀的原因,测量的数值肯定会持续不断地增大,而不可能呈现正态分布.根据这些测量值绘制出的图形会立刻反映出这种附加的因素.
正态曲线曾被无数次使用于测量天文距离,用于测量质量、力和速度;用于确定物质的熔点、沸点、结冰点的温度以及其他上百种化学性质.因为它在清除测量中的错误时具有重要作用,所以正态曲线也常常被人称为“误差曲线”.奇妙的是,误差曲线的存在揭示了一个看起来好像是悖论,然而却是真实的结论:测量中的误差(随机误差)并非随意出现,而总是表现为正态曲线.
大约在1833年,比利时统计学家凯特勒利用正态曲线研究人的生理特征及能力的分布.他使用的数据大部分取自于文艺复兴时期的一些著名艺术家对人体各部位所作的上千次测量.凯特勒及其数百名后继者的研究发现:人类几乎所有的精神和物理的特征都符合正态分布.手脚的长度、身高、体重、头颅的大小、脑的重量,由智力测验测得的智力,眼睛对电磁光谱中可见光部分的每段频率的反应灵敏度,等等,所有这些特征在一个种族或民族之内,都表现为正态分布.即使动物、矿物、植物也同样如此.例如,任何一种苹果的重量和大小也都是正态分布.
凯特勒还注意到,测量的次数越多,个体的变化就越不突出,人类的主要特征的趋向也就更加显著.每个这种特征的中间值,就等同于理想的或“平均的人”.而且,平均的人就是一个引力中心,整个社会都环绕他旋转.
对于人的特征和才能也显正态分布,凯特勒给出的解释是:所有的人就像面包一样,都是从同一个模型中制造出来的.不同之处仅仅在于,在创造过程中,发生了某些意外的变化.正是由于这个原因,所以人类会呈现出与测量中的误差分布相同的正态分布.自然界想创造完美的人,但是失败了,于是在每一方面都出现了一些误差.
现在人们深信,任何物理的或精神方面的能力分布都一定是正态分布.这种信念根深蒂固.在对大量的人所进行的任何测试中,如果结果不符合正态分布,就会遭到怀疑.例如,对一批人进行一次新的智力测试,而测试成绩没有呈现正态分布.在这种情况下,人们不会怀疑关于智力呈正态分布的结论,而是会认为这次测试失败.
关于分布图形的研究,还可引出一些非常有趣的问题和结论.我们已经知道,关于精神的和物质的特征都表现为正态分布.可是,如果我们根据社会上各种收入与具有这些收入的人的数量关系,就可描绘出一幅收入分布图形,这个图形很可能如图5.7所示.这条曲线说明,大多数人都处于低收入水平,只有少数人属于高收入阶层.事实上,相关研究表明,最普遍的收入即大众收入,处于仅能维持生计的水平.

图5.7 收入分布图
显而易见,收入分布图形与人类能力分布图形有很大的不同.人的能力分布图是正态分布,而收入分布图则表现为严重的偏态分布.于是,由此就可引出一个十分重要的社会问题:为什么收入的分布与挣得这些收入的人的能力的分布,两者之间会有如此巨大的差异呢?
现在世界各国都十分重视孩子的教育.有一个10岁男孩,在一次智力测验中测得的智商(IQ)为166分,他的父母知道这是一个很高的得分,因此千方百计为他寻找合适的特殊教育.我们已经知道,人的智商呈正态分布.我们先讨论如何应用正态分布计算其概率,然后才能真正弄清这个166是多么杰出的一个分数.
在平均值为μ、标准差为σ的正态分布中,若令μ=0,σ=1,则可得到最简单的正态分布,记作N(0,1),其密度函数为
![]()
N(0,1)称为标准正态分布,其图形如图5.8所示.
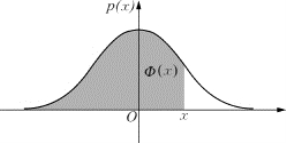
图5.8 标准正态分布
若用Φ(x)表示图5.8中的阴影部分的面积,则有
![]()
Φ(x)是N(0,1)的分布函数,人们制作了标准正态分布函数的数值表以便查用,见附录2.
例1 设随机变量ξ服从标准正态分布N(0,1),求:
(1)P(ξ<1.5); (2)P(1<ξ<2).
解 (1)由分布函数的定义可知
P(ξ<1.5)=Φ(1.5).
查附表可得Φ(1.5)=0.9332.
故P(ξ<1.5)=0.9332.
(2)由图5.9所示的简图可知
P(1<ξ<2)=Φ(2)-Φ(1).
查附表可得
Φ(2)=0.9772,Φ(1)=0.8413
故P(1<ξ<2)=0.9772-0.8413=0.1359.
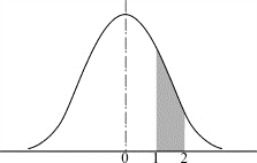
图5.9 例1(2)简图
例2 设随机变量ξ服从标准正态分布N(0,1),求P(-1.5<ξ<1).
解 由图5.10所示的简图可见:
P(-1.5<ξ<1)=Φ(1)-Φ(-1.5)=Φ(1)-[1-Φ(1.5)]=0.8413-(1-0.9332)=0.7745.

图5.10 例2简图
说明 在标准正态分布函数的数值表中虽然未列出Φ(-x)的值,但是由标准正态分布的对称性,以及分布曲线下方的面积为1,可以得到
Φ(-x)=1-Φ(x).
利用标准正态分布可以计算任意一个正态变量ξ的概率值,而不论μ和σ取何值.若ξ是非标准正态变量,只要先将变量ξ标准化,即令![]() ,则Z是一个标准正态变量,服从分布N(0,1).
,则Z是一个标准正态变量,服从分布N(0,1).
若ξ~N(μ,σ2),要求P(a<ξ<b),则将要求的概率化为
![]()
即
![]()
由于Z~N(0,1),故
![]()
例3 设随机变量ξ服从N(349.2,42),求P(ξ<340).
解 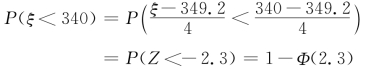
=1-0.9893=0.0107.
现在回到智商166分的那个男孩的情况.我们或许要问,总体中有多大比例的孩子可能有如此高的智商.也就是说,要求P(ξ>166)的值.根据资料可以知道智商分数的均值是100,标准差是15,把智商分数标准化可得
![]()
查标准正态分布表可得,这个概率小于0.00003.因此,总体中智商超过166分的人极少,每10万人中只有3人.
下面我们来讨论,如何借助正态分布将学生的考试分数划分成若干等级.根据经验,一般总是认为学生的考试分数服从或者近似地服从正态分布N(μ,σ2).因此,在一次考试以后,教师就可以将分数超过μ+σ的评为A等,分数在μ到μ+σ之间的评为B等,分数在μ-σ到μ之间的评为C等,分数在μ-2σ到μ-σ之间的评为D等,而将分数低于μ-2σ的学生评为F等.那么按照这样的分等方法,各个等第占总体的百分比是多少呢?
我们可以进行下列计算:
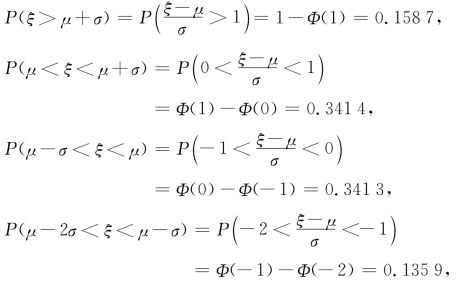

因此可以知道,在这次考试中能获A等的学生约占16%,B等约占34%,C等约占34%,D等约占14%,F等约占2%.
只要某一个随机变量是大量相互独立的偶然因素的和,而且每个因素的个别影响几乎都是极其微小,那么就可断定,这个随机变量服从或近似地服从正态分布.因此,正态分布的应用非常广泛,对它的研究也显得特别重要.
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。
















