利用边角关系解三角形

胡同文^[1]

[摘　要] 高考考生在考场上能否顺利解决三角形问题，关键在于是否理清了三角形中边与角的关系。本文以2013年高考部分三角形题为例，将三角形问题中存在的边角关系，归类为正弦定理、余弦定理、面积问题适用的边角关系以及三角关系等四个问题，以帮助考生复习三角形内容，提高解题技巧。

[关键词] 高考；数学；解三角形；边角关系

三角形问题是数学高考的必考内容，题型较为固定，2013年在全国各地高考题中都有出现。若考生在解决三角形问题时思路不对，没有理清三角形中正弦定理、余弦定理适用的边角关系和三角关系，会在高考考试中浪费考试时间，影响高考数学成绩。

一、正弦定理适用的边角关系

1. 问题描述

在三角形问题中，已知三角形的两边一角求角，两角一边求边，把已知和结论放到一起，就变成了两边两角问题，用正弦定理：s（R为三角形外接圆的半径）解决。变形形式a↔2RsinA,b↔2RsinB,c↔2RsinC ，即可以将边转化为角的正弦，也可以将角的正弦转化为边。

2. 题例

例1（2013年高考湖南理科卷第3题）

在锐角△ABC中，角A，B所对的边长分别为a，b，若2asinB=3b，则角A等于（　 ）。

分析：题中已知边a，b，sinB求角A，放在一起就是边a与角A、边b与角B的关系，使用正弦定理将边化角变形得：

2sinAsinB=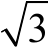3sin B

所以sinA=。因为ABC为锐角三角形，所以A=。答案：D。

例2（2013年高考北京理科卷第15题）

在△ABC中，a=3，b=26，∠B=2∠A。

（I）求cosA的值；（Ⅱ）求c的值。

分析：题（I）中关系转化为边a与角A，边b与角B的关系，所以使用正弦定理得：

sinB=sin2A=2sinAcosA

所以b=2acosA，代入得cosA=。题（Ⅱ）答案略。

例3（2013年高考辽宁理科卷第6题）

在△ABC，内角A，B，C所对的边长分别为a，b，c，asinBcosC+csinBcosA= 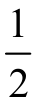b，且a＞b，则∠B=（　　）。

分析：题中条件有边a，b，c，角A，B，C，使用正弦定理变形将边化角得：

sinAsinBcosC+sinCsinBcosA=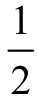sinB ，

得sinAcosC+sinCcosA=sin(A+C)=sinB =，

因为a＞b，所以B=。

二、余弦定理适用的边角关系

1. 问题描述

在三角形问题中，已知三角形的三边求角，两边一角求边，把已知和结论放到一起，就变成了三边一角问题，用余弦定理解决：a2=b2+c2+2bccosA ， b2=a2+c2+2accosB ，c2=a2+b2+2abcosC 。

变形形式：

2. 题例

例4（2013年高考上海理科卷第4题）

已知△ABC的内角A，B，C所对的边分别为a，b，c，若3a2+2ab+3b2-3c2=0，则角C的大小是_______（结果用反三角函数值表示）。

分析：题中条件有边a，b，c求角C，归类为三边一角的关系，用余弦定理变形形式，得cosC=。答案：C=π-arccos。

例5（2013年高考重庆理科卷第20题）

在△ABC中，内角A，B，C的对边分别是a，b，c，且a2+b2+2ab=c 2，

（1）求C；（2）设cosAcos，求tanα的值。

分析：题（1）条件有边a，b，c求角C，归类为三边一角关系，用余弦定理可得答案。题（2）答案略。

例6（2013年高考山东理科卷第17题）

设△ABC的内角A，B，C所对的边分别为a，b，c，且a+c=6，b=2，cosB=，

（Ⅰ）求a，c的值；（Ⅱ）求sin(A-B)的值。

分析：题（Ⅰ）中条件有边a，b，c，角B，归类为三边一角关系，用余弦定理得答案a=3，c=3；题（Ⅱ）答案略。

三、面积问题涉及的边角关系

1. 问题描述

在三角形问题中，经常涉及三角形的面积问题，由面积公式：S=2absinC =2acsinB=2bcsin A可以知道，面积公式可归类为三角形的两边一角问题和三边一角问题，这些都可以看作是同一类问题。在遇到三角形的面积问题的时候，我们需要将面积公式和余弦定理进行套用，即，会起到很好的简化效果。

2. 题例

例7（2013年高考新课标版Ⅱ卷理科第17题）

△ABC在内角A，B，C的对边分别为a，b，c，已知a=bcosC+csinB，

（Ⅰ）求B；（Ⅱ）若b=2，求△ABC面积的最大值。

分析：题（Ⅰ）中出现的条件有边a，b，c，角B，C，采用正弦定理将边转化为角，化简可得B= ；题（Ⅱ）中条件有边b，面积S，角B，归类为典型的三角形面积问题，利用面积公式和余弦定理公式套用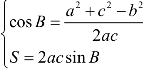进行转化，再用基本不等式可得S的最大值为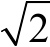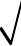2+1。

四、三角关系

1. 问题描述

在三角形问题中，已知三角形的三角，求其他的量，这一类问题就归类为角的转化问题，将其中的一角或两角进行转化。由三角和A+B+C=π可推出化简公式：

sin(A+B)=sinC ，sin(B+C)=sin A ，sin(A+C)=sin B；

cos(A+B)=-cosC ，cos(B+C)=-cos A ，cos(A+C)=-cos B。

2. 题例

例8（2013年高考江西理科卷第16题）

在△ABC中，角A，B，C所对的边分别为a，b，c，已知cosC+(cosA-3sinA) cosB=0，

（1）求角B的大小；（2）若a+c=1，求b的取值范围。

分析：题（1）中条件有角A，B，C，利用三角关系cosC=-cos(A+B)将角C转化成角A和B，再进行化简处理，答案；题（2）中条件由边a，c，求边 b，三边关系用余弦定理即可求解。

例9（2013年高考四川理科卷第16题）

在△ABC中，角A，B，C的对边分别为a，b，c，且

（Ⅰ）求cosA的值；（Ⅱ）若a=42，b=5，求向量 在方向上的投影。

分析：题（Ⅰ）中出现的条件有角A，B，C，利用倍角公式和三角关系cos(A+C)=-cosB 转化后可得cosA=-，题（Ⅱ）略。

☆ 本文原载于《课程教育研究》2014年第35期，略有改动。

【注释】

[1]【作者介绍】胡同文，1986年生，男，汉族，四川犍为人，任教于四川省成都市新津县华润高级中学，中学一级教师。