雕塑与数学

第二节　雕塑与数学^[2]

我要从人类原始的数学文化中发掘材料，用我的雕塑把这些数学信息送向遥远的未来。

——海拉曼・费古生

一、基于数学观念与形式的雕塑

当过17年数学教授的著名美国雕塑家海拉曼・费古生（Helaman Ferguson，1940—）的雕塑作品“NC脐带环”（图1-2-1），是一个青铜雕塑，看起来像玛雅或古代中国废墟中挖掘出来的古代文物。这个雕塑周边被抛光，环的表面似乎篆刻着中国古代的鼎文。其实它是一个完美的数学作品。这一雕塑的截面是数学中的圆内旋轮线（图1-2-2），它是大圆内，半径为大圆半径1/3的小圆上的一点，当小圆沿大圆圆周在大圆内滚动一周所形成的轨迹。其表面是6阶段近似的皮亚诺（Giuseppe Peano，1858—1932）曲线。

图1-2-1

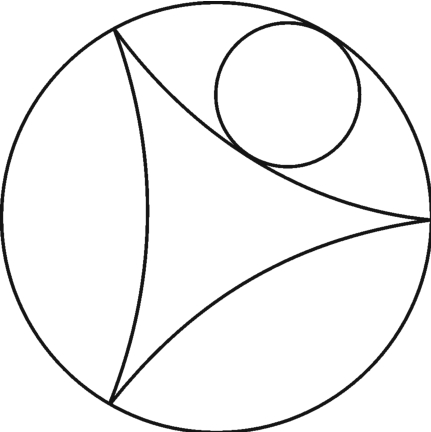
图1-2-2

皮亚诺曲线是充满欧氏平面上正方形区域的连续曲线。首先由皮亚诺给出，然后希尔伯特（David Hilbert，1862—1943）给出了简化构造方法。只要沿着皮亚诺曲线移动，我们将经过正方形中的每一点，包括正方形边上的每一点。

希尔伯特给出的简化构造方法如下：将区间［0，1］上的闭正方形分成四个面积相等的小正方形，连接小正方形的中心得到皮亚诺曲线的第1阶段近似；把每个小正方形分成四个更小的面积相等的正方形，连接更小正方形中心点就会得到皮亚诺曲线的第2阶段近似；再把更小正方形分成四个面积相等的还要小的正方形，重复上述步骤得皮亚诺曲线的第3阶段近似……第4阶段近似（如图1-2-3所示的一张中国澳门邮票上的图案）。使用一个复杂得多的方式可以作出一条经过一个正方体的每一个点的类似的曲线。图1-2-4是第一步。

图1-2-3

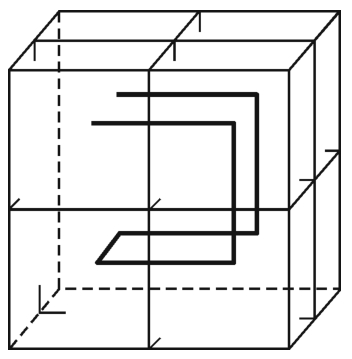
图1-2-4

经过几步希尔伯特的简化构造作图，皮亚诺曲线看起来像错综复杂的迷宫。每一步增加了路径的曲折，然而它与整个曲线相像。整个曲线是无穷长的，由无穷多的无穷小段折叠而成，人们不可能画出真正详尽的皮亚诺曲线。机械师和艺术家可以用有限宽度的切削工具来加工出有趣的印记和使人愉悦的花纹。费古生采用五阶段的皮亚诺—希尔伯特曲线作为脐带环的表面刻纹，使得其雕塑具有一个独特的有浮雕的表面——其图像像玛雅的象形文字或中国古代青铜器上的铭文（图1-2-5）。

图1-2-5

进一步指出的是，基于数学观念与形式的雕塑已产生广泛的社会文化影响，从图1-2-6至图1-2-8给出的不同国家的邮票上的图案就可略见一斑。图1-2-6中一座雕塑的形状是一个巨大的螺线，它就是巴西象征着进步的雕塑作品《扩张》。图1-2-7是一座非常引人注目的麦比乌斯带形三维雕塑作品《连续》，是由瑞士建筑师比尔创作的。它就竖立在法兰克福德意志银行的门前，由一整块80吨重的花岗岩雕刻而成。

图1-2-6

图1-2-7

麦比乌斯带是德国数学家麦比乌斯（Augustus Mobius，1790—1868）所创造的。一般的带子是由一张纸条的两端粘接而成，纸的一面成为带的内侧，而纸的另一面则成为带的外侧。如果一只蜘蛛想沿着纸带从外侧爬到内侧，那么它非得设法跨越带的边缘不可。而图1-2-8所示的麦比乌斯带，它也是由一张纸条两端粘接而成，不过，在粘接前扭转了一下。现在，所得的纸带已不再具有两面，它只有单面。这种单侧性使得不管外形被如何变形，它都不能被刺破或撕破。设想一只蜘蛛开始沿着麦比乌斯带爬，那么它能够爬遍整条带子而无须跨越带的边缘。要证实这一点，只要拿一支铅笔，笔不离纸连续地画线。那么，你将会经过整条带子，并返回你原先的起点。

图1-2-8

基于麦比乌斯带的艺术设计每年都在不断涌现。作为实用价值，麦比乌斯带的最大影响莫过于技术方面。麦比乌斯带作为汽车风扇或机械设计的传动带，在工业上有着特殊的重要性，它比传统的传动带，在磨损方面，表现得更加均匀。还有记录声音的麦比乌斯带已由弗利斯特（Forrester）于1923年设计出来了，同样思路也可用于录像带，等等。

二、雕塑的文化意义

费古生认为“雕塑是数学传播的有效途径；数学是雕塑设计的清晰语言”。他的雕塑使不是数学家的大众来体会数学家从事数学工作的愉快和那种美妙的感受。“我试图表示人类文化中最美丽的成就。”费古生说，“它们是蕴藏着的知识，但它们不应该一直躲藏在后面。”明显地，他的作品不仅传播了数学的视觉美、对称与和谐，而且表达了数学的韵味和情感。这些作品对于艺术家、数学家和参观者都是一种熏陶和启迪。在费古生的作品中，数学内在的符号化与艺术内在的符号化相互碰撞和交织。他的数学信息在许多方面使人产生共鸣。在一件雕塑作品中，人们可以清晰地看到，数学定理是怎样起作用的以及数学的永久性。现在费古生许多包含数学内容的雕塑分布在美国各地，包括于1988年创作的静静地坐落在罗得岛省美国数学会总部门前的广场上，为庆祝美国数学会成立100周年的雕塑“花托”（图1-2-9，这一具有凹槽的造型优美的雕塑，是花托、十字帽和向量场的组合）。费古生说：“我要从人类原始的数学文化中发掘材料，用我的雕塑把这些数学信息送向遥远的未来。”

图1-2-9

另一位用氖光灯管做材料从事艺术工作的女雕塑家哈立爱特・勃列森（Harriet Brisson）说：“我的许多工作是根据数学原理来做的，我发现无论从艺术的角度还是视觉的角度来看，数学图形是丰富的源泉。”今天，雕塑家们依靠数学思想来扩充艺术的例子比比皆是。托尼・罗宾（Tony Robbin）利用对拟晶体几何、第四维几何和计算机科学的研究来发展和扩充他的艺术（Pappas，1999）。三叶形扭结、环面、球形、向量、流、运动——这些是存在于赫拉曼・弗格森的雕塑中的几种数学概念。我们时常听说艺术家利用数学概念来增加他们作品的魅力。数学家、艺术家赫拉曼・弗格森在他的非凡的雕塑中传递出数学的美。他是这样说的：“数学既是艺术形式又是科学……我相信把数学沿着美学渠道传达给一般听众是行得通的。”赫拉曼用来创造他的精美形式的方法来自传统雕塑、计算机和数学方程。他的作品的名称有：《野球》、《带有十字形帽和向量场的克莱因瓶》、《带有向量场的脐点环面》等。不管是什么样的雕塑，里面都存在着数学。虽然它在被设想出来和创造成功时可以不用数学思维，然而数学存在于那件作品中，正像它存在于自然界万物中一样。

世界著名雕塑大师罗丹（Rodin）曾说过这么一句叫世人感到惊讶，让数学家感到自豪的话：“我不是一个梦幻者，而是一个数学家，我的雕塑之所以好就因为它是几何学的。”并说：“我可以在所有场合去发现立体因素，在我看来，平面和体积是所有生命的法则与美的法则。”许多艺术家都认为，罗丹的这段话显示了他对雕塑艺术的深刻理解。雕塑的美“存在于对体积的操纵与数的构成之间的关系之中”。

参考文献

［1］［美］伊凡斯・彼得生．数学与艺术——无穷的碎片［M］．袁震东，林磊译．上海：上海教育出版社，2007：22－32．

［2］袁震东．数学与雕塑［J］．数学教学，2006（9）：30，43．

［3］［美］T．帕帕斯．数学的奇妙［M］．陈以鸿译．上海：上海科技教育出版社，1999：72．

［4］［英］罗宾・J．威尔逊．邮票上的数学［M］．李心灿，邹建成，郑权译．上海：上海科技教育出版社，2002：102．