从逆向问题到逆向思维

情况简介

这是2008年我上的一节区级公开课，也是上海市市级规划项目课题《高中生数学思维障碍的分析、诊断与克服》（2005年立项）面向全区教研室开设的科研成果推广课。

文化教育价值

1.方法的简洁：

正难则反，运用逆向思维可以化繁为简。

2.哲学的思辨：

正向与逆向辩证统一。

3.情感体验：

运用逆向思维解决问题，与诗句“众里寻他千百度，蓦然回首，那人却在灯火阑珊处”的心境产生共鸣。

教学设计

教学目标：

回顾、巩固课本上有关“逆”的基本概念“逆运算”、“互逆命题”等；

知道什么是“逆向问题”，并学会提出一个有意义的“逆向问题”；

灵活运用逆向思维解题，有助于培养学生深刻性、全面性、灵活性等思维品质。

教学重点与难点：

提出一个有意义的“逆向问题”；

通过具体数学问题体会逆向思维。

教学过程：

1.“逆向”溯源

对“逆向”来一个追根溯源，我们发现，在高中数学教材上接触过有关“逆”的概念有“逆运算”、“逆命题”等。

（1）逆运算：

我们知道，减法是加法的逆运算，除法是乘法的逆运算。如，复数减法是加法的逆运算，即复数a＋bi减去复数c＋di的差是指满足（c＋di）＋（x＋yi）＝a＋bi的复数x＋yi，记作（a＋bi）－（c＋di）。其中a，b，c，d，x，y∈R。

（2）逆命题：

如果一个命题的条件与结论分别是另一个命题的结论与条件，那么这两个命题成为互逆命题。如把其中一个称为原命题，那么另一个称为它的逆命题。

例1：（2006年上海卷）

在平面直角坐标系xOy中，直线l与抛物线y2＝2x相交于A、B两点。①求证：“如果直线l过点T（3，0），那么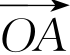·＝3”是真命题；②写出①中命题的逆命题，判断其真假，并说明理由。

这里①的证明略。在①中命题里“在平面直角坐标系xOy中，直线l与抛物线y2＝2x相交于A、B两点”是前提，“直线l过点T（3，0）”是条件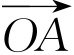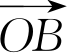，“·＝3”是结论。所以它的逆命题应为：在平面直角坐标系xOy中，直线l与抛物线y2＝2x相交于A、B两点，如果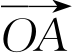·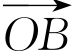＝3，那么直线l过点T（3，0）。通过举反例可知该逆命题为假命题。

明确互逆命题的这两个命题形式是随着命题的条件与结论的改变而构成的。将原命题的条件与结论互换位置就得到了它的逆命题。所以正确地写出原命题的逆命题，关键在于把握原命题中谁是条件，谁是结论即可。

在高中数学中与“逆”有关的概念还有“反函数”、“充要条件”等，从这些概念上我们都能很直接地体会到“逆向”的数学思想。

2.逆向问题

求出一个数学问题的正确结论后，将其作为条件之一，提出与原来问题有关的新问题，我们把它称为原来问题的一个逆向问题。它是近几年高考热点研究中出现的一个新概念。

（1）给定的逆向问题

例2：（2009年上海卷·春季）

如图1，在直角坐标系中，有一组对角线长为an的正方形AnBnCnDn（n＝1，2，…），其对角线BnDn依次放置在x轴上（相邻顶点重合）。设｛an｝是首项为a，公差为d（d＞0）的等差数列，点B1的坐标为（d，0）。

①当a＝8，d＝4时，证明：顶点A1、A2、A3不在同一条直线上；

②在①的条件下，证明：所有顶点An均落在抛物线y2＝2x上；

③为使所有顶点An均落在抛物线y2＝2px（p＞0）上，求a与d之间所应满足的关系式。

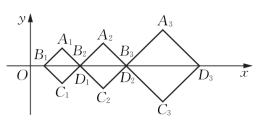
图1

给定的逆向问题是在一个数学题题目中呈现的，往往是第二小题是第一小题的逆向问题。在此例中，第③小题既是对第②小题的推广，同时也是第②小题的逆向问题。给出逆向问题，能使学生解题目标明确，引导学生感悟通过探究逆向问题来发现真理的过程，是引导学生进行研究性学习的有效手段。

（2）开放的逆向问题

开放的逆向问题指在一个数学题中，只给出原问题，而由学生自己提出一个与原问题相关的“逆向”问题。

例3：（2007年上海卷（春季））

……试给出问题“在平面直角坐标系xOy中，求点P（2，1）到直线3x＋4y＝0的距离。”的一个有意义的“逆向”问题，并解答你所给出的“逆向”问题。

明确“在平面直角坐标系xOy中”是前提，原问题的条件中有两个信息点：①“点P（2，1）”和②“直线3x＋4y＝0”。当我们求得原问题中的结论：点到直线的距离为2后，将它作为逆向问题中的条件，于是便可针对原问题的两个信息点提出各种不同的有意义的逆向问题。

针对信息点①可以提出如下逆向问题：在平面直角坐标系中，求到直线3x＋4y＝0的距离为2的点的轨迹；在平面直角坐标系中，求到直线3x＋4y＝0的距离为2且横坐标为2的点的纵坐标，等。针对信息点②可以提出如下逆向问题：在平面直角坐标系中，点P（2，1）到过原点的直线l的距离为2，求直线l的方程；在平面直角坐标系中，点P（2，1）到直线l：ax＋4y＝0的距离为2，求直线l的方程，等。

学会提出一个逆向问题，首先要明确原题中的前提，并且必须细致地分析清楚题中的各个信息点，才能对相关信息点进行有效提问。

3.逆向思维

逆向思维是指从原问题的相反角度来思考问题，引导启发思维，从而得到原问题的求解方法。在历年高考和考前训练中，运用逆向思维求解的试题也屡见不鲜。

（1）定义、公式的逆向使用

定义的表现形式是一个命题，它具有可逆性。所以我们既要熟练地正向使用定义、公式及有关定理等，同时也要重视对它们的逆向使用。

例4：（2003年上海卷）

已知数列｛an｝（n为正整数）是首项为a1，公比为q的等比数列。

①求和：

②由①的结果归纳概括出关于正整数n的一个结论，并加以证明。

对于①，逆向使用二项式定理可得：

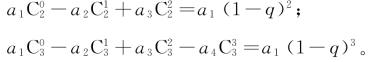
对于②，关于正整数n的一个结论为：若数列｛an｝（n为正整数）是首项为a1，公比为q的等比数列，

则

逆向使用二项式定理即可证得，证明略。

例5：（2006年上海卷）

若函数f（x）＝ax（a＞0，a≠1）的反函数的图像经过点（2，－1），则a＝________。

这里，如果直接求出f（x）的反函数f－1（x）＝logax，再用（2，－1）代入，求出a的值亦可。不过如果明确了反函数的定义，并且逆向使用反函数定义，就知道原函数f（x）的图像应该经过点（－1，2），即可求得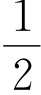

例6：（2006年陕西卷）

cos43°cos77°＋sin43°cos167°的值为_______。

原式可化为cos43°sin13°－sin43°cos13°，逆向使用两角差的正弦公式，即可得结果为－。

除了逆向使用二项式定理、反函数定义，还可对其他一些对定理、定义以及公式的逆向使用，如对基本不等式的逆向使用等等。

（2）运算与变换的可逆性

熟练运用运算的可逆性以及函数图像的平移、旋转、伸缩变换的可逆性等，可以化繁为简，找到解题的捷径。

例7：（2007年山东卷）

要得到函数y＝sinx的图像，只需将函数的图像（　　）

A.向右平移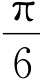个单位　　　B.向右平移个单位

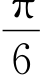C.向左平移个单位　　　D.向左平移个单位

由于，再运用图像变换的可逆性易得正确选项为A。

例8：（2007年全国卷）

设复数z满足＝i，则z＝_________。

此题不必设z＝a＋bi（a，b∈R），利用运算的可逆性有即可得z＝2－i。

（3）反证法与逆否命题的应用

在一些有关存在性、否定性、唯一性等命题的时候，往往正面直接入手很难。正难则反，反证法有时就成为一种行之有效的方法。

例9：判断命题“若空间四点不共面，则这四点中任何三点都不共线”的真假。

考虑其逆否命题：若空间四个点中有三点共线，则四点共面。易知该逆否命题是真命题，故原命题亦为真命题。

例10：若a，b，c均为实数，且求证：a，b，c中至少有一个大于0。

可采用反证法。由于结论的反面是：a，b，c均不大于0。故假设a，b，c都不大于0，即a≤0，b≤0，c≤0，则a＋b＋c≤0。

而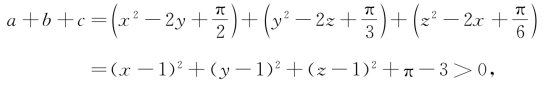

这与a＋b＋c≤0矛盾，假设不能成立，故得证。

（4）概率中的排除法与集合中的补集思想

概率中的排除法与集合中的补集思想都是逆向思维最常见的表现形式。

例11：（2008年上海市虹口区高考模拟卷）

在集合｛1，2，3，4，5，6，7，8｝中任取4个数组成的子集，如果这四个数中任取两数之和都不是9，则取出这种子集的概率为_______。

这里把取出四个数中存在两数之和为9的情况排除即可。1－

例12：已知关于x的不等式＜0的解集为M，若3∈M，5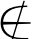M，求实数a的范围。

由于3∈M，5M，所以＜0且≥0，或52－a＝0，故可得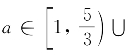（9，25］。

例13：已知下列三个方程：x2＋4ax－4a＋3＝0，x2＋（a－1）x＋a2＝0，x2＋2ax－2a＝0，其中至少有一个方程有实根。求实数a的取值范围。

问题的反面是：三个方程都没有实根。我们先求出三个方程均没有实根时，求得故原题实数a的取值范围是a∈

（5）反客为主的逆向视角

例14：（2006年江西卷）若不等式x2＋ax＋1≥0，对一切x∈（0）成立，则a的最小值是_______。

这里我们可以反客为主，将原不等式看成关于a的一元一次不等式：当时，有则所以a的最小值是－。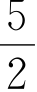

从上例，我们可以发现字母a原是不等式中的一个参数，而直接将原不等式看成是关于x的不等式，而用一元二次方程根的分布理论去解的话就过于烦琐。而当我们变换视角，主客倒置，将不等式看成关于a的一元一次不等式就能轻松应对。

（6）执果索因的思想方法

在探讨有关因果关系的问题时，往往先知道结果，然后才去探究其原因，这一探究的过程成为“执果索因”。

例15：已知集合A＝｛－4，－2，3，8｝。①试写出一个形如ax＋b＞0（a≠0）的关于x的不等式，使得它的解集与集合A有且只有一个公共元素；②试写出一个一元二次不等式，使得它的解集与集合A有且只有一个公共元素。

对于①，不妨找一个解集为（6，＋∞）的一元一次不等式，使得它与集合A有且仅有一个公共元素8。易找到这样的一元一次不等式，如：x－6＞0等。对于②，不妨找一个解集为（－∞，－8）∪（6，＋∞）的一元二次不等式，这样它与集合A有且仅有一个公共元素8。易找到这样的一元二次不等式，如：（x＋8）（x－6）＞0等。

在此中我们是拿着不等式的解集去找不等式。在数学中涉及执果索因的方法的还有很多例子，解题或证明中采用的分析法便是又一个例证。

4.回顾小结

从掌握课本上有关“逆”的基本概念“逆运算”、“互逆命题”等，到学会提出一个有意义“逆向问题”，最终希望学生达到较高的思维层次要求，学会逆向思维。当我们在致力于研究一个问题，正向思考颇费周折的时候，不妨正难则反，采取逆向思维，就会“骤然回首，豁然开朗”。经常训练有关逆向问题，如：研究逆命题并判断真假，合理地提出逆向问题，同时经常训练学生采用逆向思维的解题方法，有助于培养学生深刻性、全面性、灵活性等思维品质，有利于相关思维障碍的克服。

5.作业布置（略）

教学设计说明

有关“逆”，学生一直比较陌生，而且在解决数学问题的时候学生更多的是想到正面进攻，一般都不会想到去逆向出击。

正值自己研究关于思维障碍的课题，所以设计了这样一堂关于逆向思维的课。本课的设计主要从学生已有的经验出发，然后逐步过渡到逆向思维阶段。

本课经历了从逆运算、逆命题，到逆向问题，再到逆向思维三个阶段，这三个环节层层递进。

1.关于“逆运算与逆命题”

学生对逆运算和逆命题应该不会陌生。这一环节的设计主要是让学生从已有的数学经验出发，有一个对“逆”的大致体验。

2.关于“逆向问题”

逆向问题曾一度成为高考热点。在开放的逆向问题中，学生对原问题提出一个逆向问题的能力还很欠缺。在这节课中，具体解读如何提出逆向问题，关键是把握好原问题中的一些信息点，至于解决逆向问题则不是本课的重点。

3.关于“逆向思维”

逆向思维是一种解决数学问题的手段。逆向思维有很多具体的形式。在本课中虽然例题看似较多，但题目本身难度并不高。主要目的是要让学生通过一些具体的例题来了解形式各异的逆向思维。故本课重点在于对逆向思维的体会，以期达到能灵活使用逆向思维解题的目的，从而促进学生深刻性、全面性、灵活性等思维品质的发展。

关于逆向思维，本课在以下六个方面分别做出解读，并给出实例加以具体说明。①定义、公式的逆向使用；②运算与变换的可逆性；③反证法与逆否命题的应用；④概率中的排除法与集合中的补集思想；⑤反客为主的逆向视角；⑥执果索因的思想方法。

我们一般都提倡在讲解数学知识或数学问题的时候，将数学的思想方法润物细无声地渗透给学生。不过当“渗透”无法酝酿出足够的力量时，我们不妨就高举逆向的旗帜，来一次关于逆向思维教学的正面出击。这堂课就是对逆向思维教学的一次主动出击。这样的直面出击能有助于使逆向思维更为惹人注目，从而加深印象，以至刻骨铭心。

课例点评

“反其道而行之”，让思维从问题的相反面的方向发展。比如，司马光砸缸的故事中，当小伙伴跌进水缸里时，其他孩子都在想怎样把他从水里救出来，而司马光却独自从相反的方向思想，把“救人离水”变为“让水离人”，这样的思维方式就是逆向思维。逆向思维与常规思维（顺向思维）的不同之处，就是反过来思考问题，用绝大多数人没有想到的方法去解决问题。

本节课是徐泼老师领衔的市级规划课题“高中学生数学思维障碍的分析、诊断与克服”成果鉴定与展示活动中的一节课。徐教师针对当前数学教学中的热点问题“逆向问题与逆向思维”组织教学，她敢于上这节课，说明了她对这一问题的研究是深入的，也是卓有成效的。

在数学中，不少概念都包含着“逆”的含义，加法与减法、乘法与除法、乘方与开方等都是互“逆”的运算；原命题与它的逆命题，是条件与结论相逆的命题；原函数与反函数，是由一对逆映射决定的。学生对这些都是有所了解的。在小学生学习减法和除法时，6－2等于几，6÷3等于几，教学时都是引导学生用逆向思维来思考的。另外，“正难则反”的思维方法，学生也经常在自觉或不自觉地运用。

徐老师在课上讲的是“逆向问题”，这是与“逆命题”不同的一类问题，也是近年来高考中的一个热点问题。“逆命题”，只要把条件与结论对换就行了，而“逆向问题”是把题目中的结论作为条件，能推得什么样的结论，这种问题是开放的，因为把原来问题中的结论作为条件后，得到的新的结论不一定是原来的条件，学生在学过条件的充分性与必要性后都知道这一点。所以，这节课上师生的思维层次是比较深的。

徐老师在课堂上选择的问题都是近年来高考中的一些典型题目，对“逆向问题——逆向思维”开展了探究与讨论，由浅入深，对逆向问题与互逆问题的联系与区别作了阐述，对“执果索因”的逆向思维方法进行了概括。课堂上讨论的问题比较多，容量很大，但在教师的正确引导下，学生在学习过程中，能积极投入，勇于探究，热烈讨论。使问题一个个得到较好的解决。因而，我们认为本节课是体现高三复习中的研究性学习的一节好课。这节课也是徐老师多年来潜心研究的结晶与成果。

嘉定区教师进修学院　张桂明（教研员）