剖析高考数学中的恒成立问题
于先锋
新课标下的高考越来越注重对学生的综合素质的考查,恒成立问题便是一个考查学生综合素质的很好途径,也是数学高考中的难点。它主要涉及到一次函数、二次函数等函数的性质、图象,渗透着换元、化归、数形结合、函数与方程等思想方法,在培养学生思维的灵活性、创造性等方面也起到了积极的作用。近几年的数学高考中频频出现恒成立问题,其形式逐渐多样化。
解决高考数学中的恒成立问题常用以下几种方法:①函数性质法;②主参换位法;③分离参数法;④数形结合法。下面我就以近三年高考试题为例加以剖析:
一、函数性质法
1.二次函数:
①若二次函数f(x)=ax2+bx+c(a≠0)>0(或<0)在R上恒成立,则有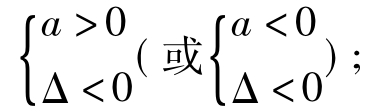
②若二次函数f(x)=ax2+bx+c(a≠0)>0(或<0)在指定区间上恒成立,可以利用韦达定理以及根的分布等知识求解。
例1(2008年江西卷理12) 已知函数f(x)=2mx2-2(4-m)x+1,g(x)=mx,若对于任一实数x,f(x)与g(x)的值至少有一个为正数,则实数m的取值范围是( )
A.(0,2) B.(0,8) C.(2,8) D.(-∞,0)
分析:f(x)与g(x)的函数类型,直接受参数m的影响,所以首先要对参数进行分类讨论,然后转换成不等式的恒成立的问题利用函数性质及图像解题。
解析:当m=0时,f(x)=-8x+1>0在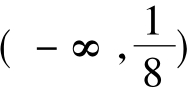 上恒成立,而g(x)=0在R上恒成立,显然不满足题意;(如图1)
上恒成立,而g(x)=0在R上恒成立,显然不满足题意;(如图1)
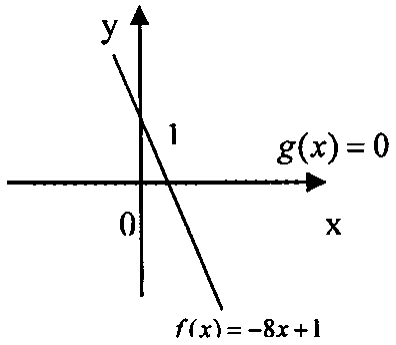
图1
当m<0时,g(x)在R上递减且g(x)=mx>0只在(-∞,0)上恒成立,而f(x)是一个开口向下且恒过定点(0,1)的二次函数,显然不满足题意。(如图2)
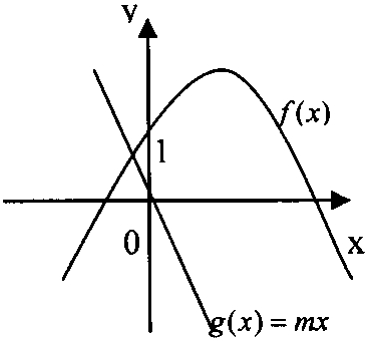
图2
当m>0时,g(x)在R上递增且g(x)=mx>0在(0,+∞)上恒成立,而f(x)是一个开口向上且恒过定点(0,1)的二次函数,要使对任一实数x,f(x)与g(x)的值至少有一个为正数则只需f(x)>0在(-∞,0)上恒成立。(如图3)

图3
则有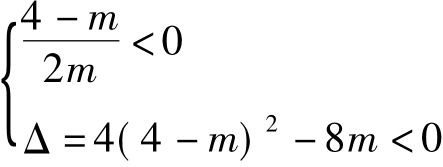 或
或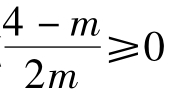 解得4<m<8或0<m<4,综上可得0<m≤8即m∈(0,8)。故选B。
解得4<m<8或0<m<4,综上可得0<m≤8即m∈(0,8)。故选B。
例2(2009年江西卷文17) 设函数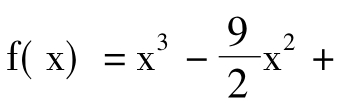 6x-a.
6x-a.
(1)对于任意实数x,f'(x)≥m恒成立,求m的最大值。(节选)
解析:(1) f'(x)=3x2-9x+6,∵对A x∈R,f'(x)≥m,即3x2-9x+(6-m)≥0在 x∈R上恒成立,∴Δ=81-12(6-m)≤0,得m≤-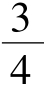 ,即m的最大值为-
,即m的最大值为- 。
。
2.其他函数:
f(x)>0恒成立→f(x)min>0(注:若f(x)的最小值不存在,则f(x)>0恒成立→f (x)的下界大于0);f(x)<0恒成立→f(x)max<0(注:若f(x)的最大值不存在,则f(x) <0恒成立→f(x)的上界小于0).
例3(2007年重庆卷理20) 已知函数f(x)=ax4 ln x+bx4-c(x>0)在x=1处取得极值-3-c,其中a、b为常数.
(1)试确定a、b的值;
(2)讨论函数f(x)的单调区间;
(3)若对任意x>0,不等式f(x)≥-2c2恒成立,求c的取值范围。
分析:f(x)≥-2c2恒成立,即f(x)min≥-2c2,要解决此题关键是求f(x)min,x>0。
解:(1)(2)略
(3)由(2)知,f(x)在x=1处取得极小值f(1)=-3-c,此极小值也是最小值.
要使f(x)≥-2c2(x>0)恒成立,只需-3-c≥-2c2,即2c2-c-3≥0。
从而(2c-3)(c+1)≥0。解得c≥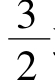 或c≤-1。
或c≤-1。
∴c的取值范围为(-∞,-1]∪[ ,+∞)。
,+∞)。
例4(2008年天津文21) 设函数f(x)=x4+ax3+2x2+b(x∈R),其中a,b∈R。
(Ⅲ)若对于任意的a∈[-2,2],不等式f(x)≤1在[-1,1]上恒成立,求b的取值范围。(节选)
分析:f(x)≤1,即f(x)max≤1,a∈[-2,2],x∈[-1,1],要解决此题关键是求f (x)max。
解:(Ⅲ) f'(x)=4x3+3ax2+4x=x(4x2+3ax+4)由条件a∈[-2,2]可知Δ=9a2-64<0,从而4x2+3ax+4>0恒成立.当x<0时,f'(x)<0;当x>0时,f'(x)>0。
因此函数f(x)在[-1,1]上的最大值f(1)是f(-1)与两者中的较大者。
为使对任意a∈[-2,2],不等式f(x)≤1在[-1,1]上恒成立,当且仅当f(x)max≤1,即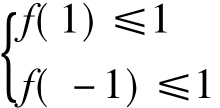 ,即
,即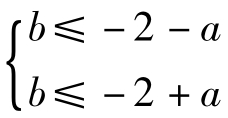 在a∈[-2,2]上恒成立.即
在a∈[-2,2]上恒成立.即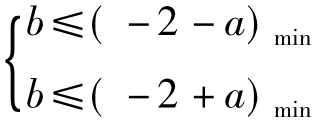 ,a∈[-2,2]
,a∈[-2,2]
所以b≤-4,因此满足条件的b的取值范围是(-∞,-4]。
则由题意得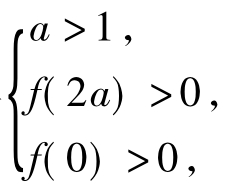 即
即 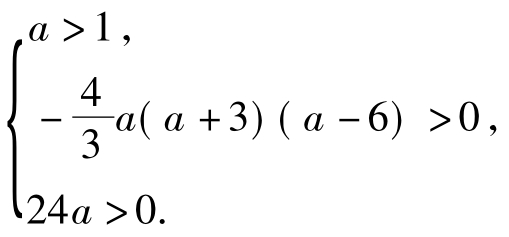 解得1<a<6
解得1<a<6
∴a∈(1,6)。
二、主参换位法
某些含参不等式恒成立问题,在分离参数会遇到讨论的麻烦或者即使能容易分离出参数与变量,但函数的最值却难以求出时,可考虑变换思维角度。即把主元与参数换个位置,再结合其他知识,往往会取得出奇制胜的效果。
例5(2007年辽宁卷文科22) 已知函数f(x)=x3-9x2 cosα+49x cosβ+18sin2α,g(x)=f'(x),且对任意的实数t均有g(1+cos t)≥0,g(3+sin t)≤0。
(Ⅰ)求函数f(x)的解析式;
(Ⅱ)若对任意的m∈[-26,6],恒有f(x)≥x2-mx-11,求x的取值范围。
解析:(Ⅰ)g(x)=f'(x)=3x2-18x cosα+48cosβ,A t∈R,0≤1+cos t≤2,2≤3+sin t≤4,而g(1+cos t)≥0,g(3+sin t)≤0恒成立.则由二次函数性质得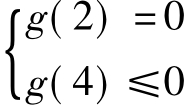 ,解得cosα=1,cosβ=
,解得cosα=1,cosβ=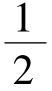 ,sinα=0.∴f(x)=x3-9x2+24x。 (Ⅱ) f(x)≥x2-mx-11→mx-9x2+24x+11≥0.令h(m)=mx-9x2+24x+11,
,sinα=0.∴f(x)=x3-9x2+24x。 (Ⅱ) f(x)≥x2-mx-11→mx-9x2+24x+11≥0.令h(m)=mx-9x2+24x+11,
则f( x)≥x2-mx-11即h(m)≥0.由于m∈[-26,6],则有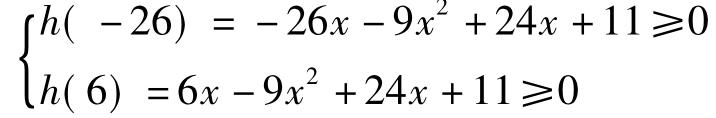 解得-
解得-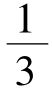 ≤x≤1。所以x的取值范围为[-
≤x≤1。所以x的取值范围为[-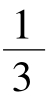 , 1]。
, 1]。
例6(2008年安徽文科20) 已知函数f(x)= ,其中a为实数.
,其中a为实数.
(Ⅱ)已知不等式f'(x)>x2-x-a+1对任意a∈(0,+∞)都成立,求实数的取值范围。(节选)
分析:已知参数a的范围,要求自变量x的范围,转换主参元x和a的位置,构造以a为自变量x作为参数的一次函数g(a),转换成A a∈(0,+∞),g(a)>0恒成立再求解。
解析:由题设知ax2-3x+(a+1)>x2-x-a+1对A a∈(0,+∞)都成立,即a (x2+2)-x2-2x>0对A a∈(0,+∞)都成立。设g(a)=(x2+2)a-x2-2x(a∈R),则g(a)是一个以a为自变量的一次函数。∵x2+2>0恒成立,则对A x∈R,g(a) 为R上的单调递增函数。所以对A a∈(0,+∞),g(a)>0恒成立的充分必要条件是g(0)≥0,-x2-2x≥0,∴-2≤x≤0,于是x的取值范围是{x|-2≤x≤0}。
三、分离参数法
利用分离参数法来确定不等式f(x,λ)≥0,(x∈D,λ为实参数)恒成立中参数λ的取值范围的基本步骤:
(1)将参数与变量分离,即化为g(λ)≥f(x)(或g(λ)≤f(x))恒成立的形式;
(2)求f(x)在x∈D上的最大(或最小)值;
(3)解不等式g(λ)≥f(x)max(或g(λ)≤f(x)min),得λ的取值范围。
适用题型:(1)参数与变量能分离;(2)函数的最值易求出。
例7(2007年山东卷文15) 当x∈(1,2)时,不等式x2+mx+4<0恒成立,则m的取值范围是________。
解析:当x∈(1,2)时,由x2+mx+4<0得m<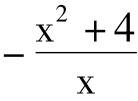 .令f(x)=
.令f(x)=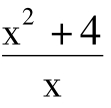 =
=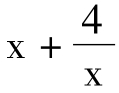 ,
,
则易知f(x)在(1,2)上是减函数,所以x∈[1,2]时f(x)max=f(1)=5,则(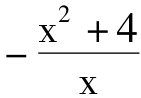 )min>-5∴m≤-5。
)min>-5∴m≤-5。
例8(2009年山东卷文21) 已知函数f(x)=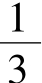 ax3+bx2+x+3,其中a≠0
ax3+bx2+x+3,其中a≠0
(1)当a,b满足什么条件时,f(x)取得极值?
(2)已知a>0,且f(x)在区间(0,1]上单调递增,试用a表示出b的取值范围。
分析:此题虽有三个变量x、a、b,而x的范围已知,最终要用a表示出b的取值范围,所以可以将看成一个已知数,对x和b进行离参。
解析:(2) f(x)在区间(0,1]上单调递增→f'(x)=ax2+2bx+1≥0在(0,1]上恒成立→b≥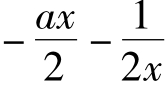 ,x∈(0,1]恒成立→b≥(
,x∈(0,1]恒成立→b≥(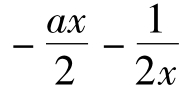 )max,x∈(0,1]。设g(x)=-
)max,x∈(0,1]。设g(x)=-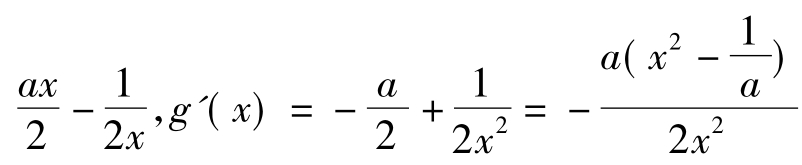 ,令g'(x)=0得x=
,令g'(x)=0得x=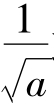 或x=
或x=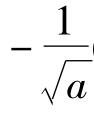 (舍去),当a>1时,0<
(舍去),当a>1时,0<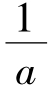 <1,当x∈(0
<1,当x∈(0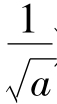 )时g'(x)>0,g(x)=
)时g'(x)>0,g(x)=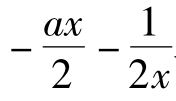 单调增函数;当x∈
单调增函数;当x∈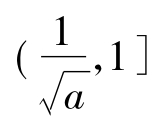 时g'(x)<0,g(x)=
时g'(x)<0,g(x)=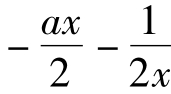 单调减函数,∴g(x)max=
单调减函数,∴g(x)max=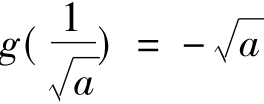 ,∴b≥
,∴b≥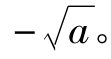
当0<a≤1时,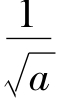 ≥1,此时g'(x)≥0在区间(0,1]恒成立,所以g(x)=
≥1,此时g'(x)≥0在区间(0,1]恒成立,所以g(x)=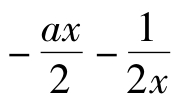 在区间(0,1)上单调递增,∴g(x)max=g(1)=
在区间(0,1)上单调递增,∴g(x)max=g(1)=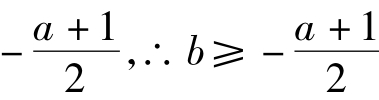 。
。
综上,当a>1时,b≥-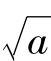 ;当0<a≤1时,b≥-
;当0<a≤1时,b≥-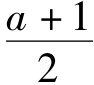 。
。
四、数形结合(对于f(x)≥g(x)型问题,利用数形结合思想转化为函数图象的关系再处理)
若把等式或不等式进行合理的变形后,能非常容易地画出等号或不等号两边函数的图象,则可以通过画图直接判断得出结果。尤其对于选择题、填空题这种方法更显方便、快捷。
例9(2007年安徽理科3) 若对任意x∈R,不等式|x|≥ax恒成立,则实数a的取值范围是
A.a<-1 B.|a|≤1
C.|a|<1 D.a≥1
解析:对A x∈R,不等式|x|≥ax恒成立
则由一次函数性质及图像知-1≤a≤1,即|a|≤1。
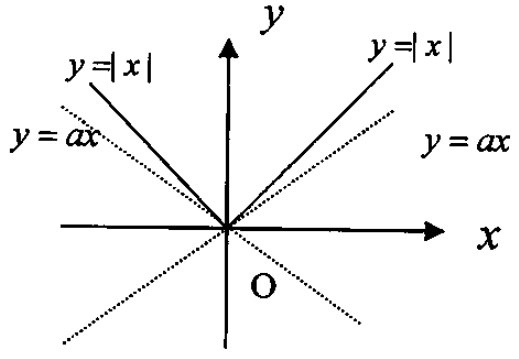
图4
上述例子剖析了近三年数学高考中恒成立问题的题型及解法,值得一提的是,各种类型各种方法并不是完全孤立的,虽然方法表现的不同,但其实质却都与求函数的最值是等价的,这也正体现了数学中的“统一美”。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。















