授人以鱼,不如教人以渔——浅淡数学教学中学生思维品质的培养
李继元
古人云:“授人以鱼,一饭之需;教人以渔,终身受用。”可见教人以方法的重要性。在数学教学中,进行学法指导、能力培养、素质提高,其核心就是发展学生的思维能力,培养学生良好的思维品质。笔者认为良好的思维品质是指思维的深刻性、敏捷性、创新性、灵活性、批判性等几个方面。它反映了人与人之间思维个性的差异,是判断智力层次,确定一个人智力水平的主要标志。因此,培养良好的思维品质是进行学法指导、能力培养的突破口,是提高学生素质的根本途径。
在教学过程中,我们应根据具体教学内容,充分挖掘教材潜力,发挥它在培养思维品质方面的重要作用。下面就以解析几何教学的几个片断为例,谈谈对学生思维品质的培养。
一、深化概念,培养思维的深刻性
思维的深刻性是指认识事物本质的能力,这种能力表现为善于思考问题、准确把握事物本质及其规律性,揭示被掩盖着的某些个别特殊情况等。教学中,不能只停留在描述知识的表面现象上,要注意引导学生善于概括归类,抓住事物的本质规律,预见事物发展的进程,把思维引向一定的深度和广度。
如在双曲线概念的教学中,当得出双曲线的概念[1]后,再通过设问:“概念中的常数为什么要小于|F1F2|,进而作如下启发,引申:
1.当常数等于|F1F2|时,点M的轨迹是什么?
2.当常数大于|F1F2|时,点M的轨迹是什么?
进而还可以引出双曲线的左支或右支与概念中“绝对值”之间的关系。
通过上述各问题的引申,使学生对双曲线概念中“绝对值”、“常数”(小于|F1F2|)就有了较深刻的认识和理解,从而培养了学生思维的深刻性,同时为概念的运用也打下了良好的基础。
二、在问题的研讨中,培养思维的创新性
思维的创新性是指独立思考创造出有用的结果或具有新颖成分的结果的智力品质,教学中应及时抓住可深入研讨的问题,积极引导学生广泛联想,探索创造,寻找一般规律,积极培养学生思维的创新性品质。
例如:在讨论直线与双曲线的位置关系时,当直线与双曲线方程联立的方程组只有一个解时,直线与双曲线只有一个公共点。那么这个公共点是交点,还是切点,事实上,通过研究和探索可知,直线L与双曲线C议程联立,消去X(或Y)得关于X的一元二次方程:ax2+bx+c=0的解与直线L和双曲线C的位置关系如下表所示:
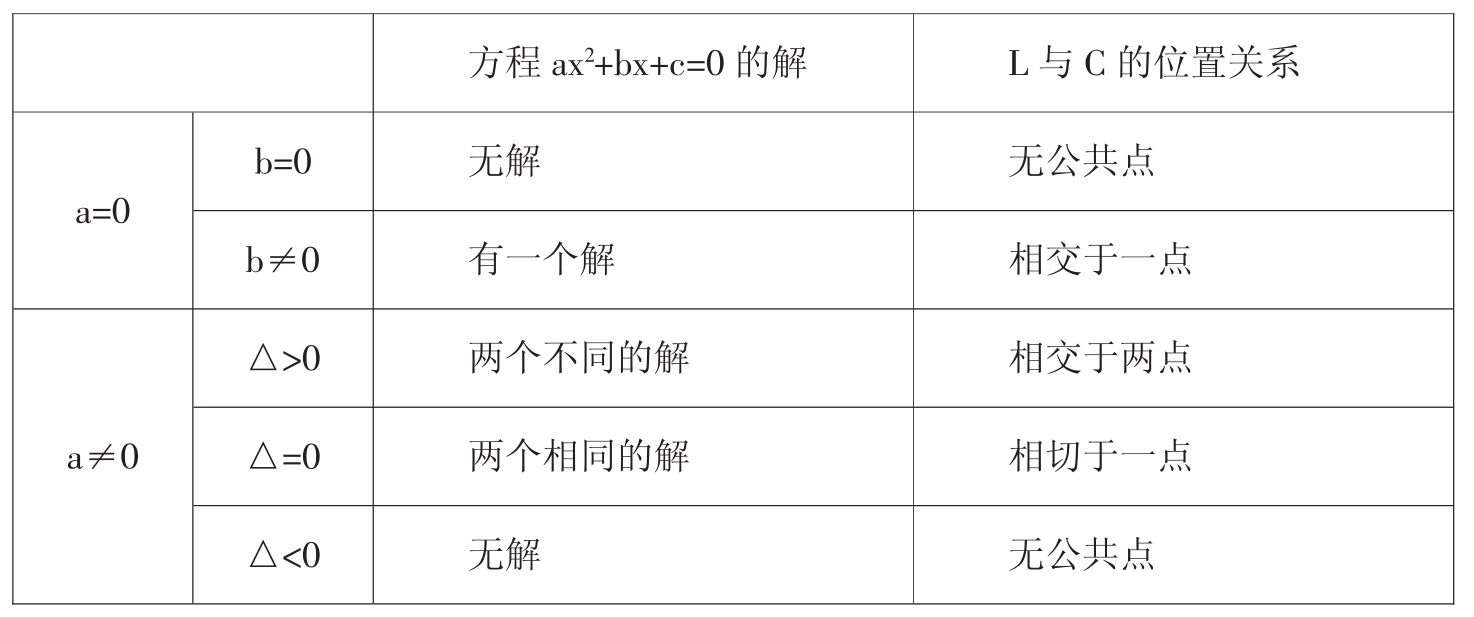
表中注一是指当L与C的渐近线时才出现这种情况;注二是指当L与C的渐近线平行时,才出现此情况。
像这样,对课本中的结论经常多问几个为什么,追本溯源,进行深入的研究探讨,以点带面,既可以使学生避免对知识的片面理解,又可以培养学生思维的创新性。
三、在概念的应用中,培养学生思维的敏捷性
思维的敏捷性是指思维过程中的简缩性和快速性,主要表现在解决问题的过程中能积极地思考、迅速地判断,并能缩短运算环节和推理过程。在教学中,我们不仅要对概念、定理、性质真正的理解,还要突出数学思维、数学方法的启示。解题时,应善于观察联系,综合分析,抽象概括。通过对概念、定理、性质在解题中的有效运用,达到训练新思维的敏捷性。
例1 设抛物线方程为Y2=2px(p>0),过抛物线焦点的直线交抛物线于A、B两点的横坐标和为m,求|AB|的值。
分析:设出直线A B的方程,与抛物线方程联立方程组,结合韦达定理求得│AB│。但运算过程较繁琐,实际上,根据A B过焦点这一特性,由抛物线概念不难得出:
AB=m+p
进而给出下列命题,让学生亲自动手解决。
命题1设椭圆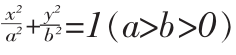 的离心率为e,且过焦点的直线交椭圆于A(x1,y1)、B(x2,y2)两点,求|AB|。
的离心率为e,且过焦点的直线交椭圆于A(x1,y1)、B(x2,y2)两点,求|AB|。
命题2设双曲线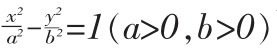 离心率为e,且过焦点的直线交双曲线于A(x1,y1)、B(x2,y2)两点,求|AB|。
离心率为e,且过焦点的直线交双曲线于A(x1,y1)、B(x2,y2)两点,求|AB|。
通过练习,让学生在概念的运用和对比中,领会问题中过焦点的直线有什么特性,总结出一般规律,提高熟练程度,从而培养了学生思维的敏捷性。
四、一题多解,一题多变,一题多联,培养思维的灵活性
思维的灵活性指能够根据客观条件的发展与变化,及时地改变先前的思维过程,寻求新的解决问题途径,能及时地摆脱思维定势束缚,在教学中,通过一题多解,一题多变,一题多联,可培养学生思维的灵活性。
例2 求过点A(3,4)且于圆C,(x-1)2+y2=1相切的直线方程。
分析:点A在圆C之外,下面引导学生从不同的角度解题。
思路一 设切点(x1,y1),则由切线性质得方程组
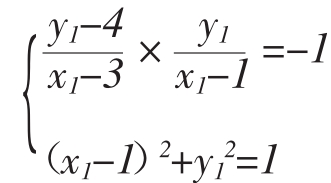
解出x1,y1,由两点式可求得切线方程。
思路二 设所求切线方程为y-4=k(x-3),与圆C方程联立方程组,消去y得:
(K2+1)x2-(6K2+8K+2)+9K2-24K+16=0,由其判别式△=0,可解得K的值,求得切线方程。
思路三 设所求切线方程为y-4=k(x-3),则圆心C(1,0)到切线的距离
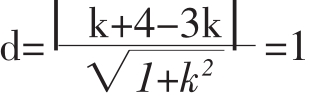
解得K的值,可求得切线方程。
相比之下,思路三最简便。通过上述多种思路分析,可使学生的思维处于一种积极的状态。在这些思路中,汇聚了大量的信息,从而拓宽了思维的领域,有效地训练了学生思维的灵活性。
进一步给出下列命题,一题多联,培养学生探求问题的个性品质。
变1求过点A(2,2)且与圆(X-1)2+y2=1相切的直线方程。
分析:注意点A在圆外,同时还应注意易漏掉切线斜率不存在的情况。
变2求过点A(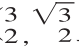 且于圆(x-1)2+y2=1相切的直线方程。
且于圆(x-1)2+y2=1相切的直线方程。
分析:点在圆上,通过垂线求切线斜率较简便。
变3求过点A(2,a)且于圆(x-1)2+y2=1相节的直线方程:
分析:注意对a取值的讨论。
通过上述一题多变,就可总结出过圆外或圆上一点与圆相切的切线方程的最简求法及注意事项。
五、设置误区,培养思维的批判性
思维的批判性,是思维活动中独立分析和批判的程度,它主要表现为善于思考,有自己的独立见解,敢于怀疑,有较高的辨别能力。在教学中,抓住具有普遍意义的典型错误,有意识地布置“陷阱”,引导学生进行错解辨析,对比类似问题在解决过程中的异同,提高学生的辨别能力和推理能力,从而达到培养思维的批判性的目的。
例3 直线L1:ax-y+2=0,与直线L2:(a+1)x-ay+1=0相垂直,则a的值为()
A、a=-2 B、a=2
C、a=-2或a=0 D、a的值不确定
教学时,笔者有意出示如下解法:
∵直线L1,L2的斜率分别为a,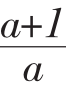
由L1⊥L2可得: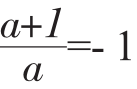
解得a=2
故:正确答案为A
然后引导学生进行辨析,得出正确答案为C,而不是A,使学生明确了产生错误的原因是忽视了直线斜率不存在的情况。
通过对上述问题的辨析,不仅使学生从“陷阱”中挣脱出来,自觉产生环境效应,更主要的是能使学生逐步培养用批判的态度来认识问题的习惯,从而使学生思维的批判性得到发展。
(1999年10月获宁夏教研室数学教学研究会二等奖)
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。
















