有一种数，在数学上称为无理数，即无限不循环小数，这种数无论计算到小数点后多少位，都无法找出它的重复循环部分，圆周率π即圆周长与直径之比就是这样一种数。这是无法用有限次加减乘除和开方等代数运算求出来的数。正因为如此，古代人民在解决圆周长、圆面积、球体积等类问题时，遇到计算π值问题，从那时起到现在，π值已经计算到小数点后几百万位了，还没有算完，当然也不会算完。
建武二十一年的斛
虽然如此，π值还是越来越精确化的。起初，人们采用的圆周率是“周三径一”，圆的半径为1，圆的周长为3，即π值取作3。这个数值当然相当粗糙，用它来进行一般计算都会产生相当大的误差，更不用说进行天文、地理的测量和计算了。随着生产和科学的发展，对π值的要求越来越精确。人们开始探索圆周率的计算。公元1世纪时，中国制造的律嘉量斛——一种圆柱形标准量器，它取的圆周率是3.1547。东汉天文学家张衡，在《灵宪》一书中取π＝730/232＝3.1466，又在球体积中取π＝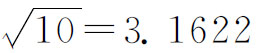
。三国时吴国人王蕃在《浑仪论》中取π＝142/45＝3.1556。这些π值虽然比π＝3的取值精确，但还都是经验的结果，而不是通过严格、科学的理论计算得出的，它没有给出π值的理论计算方法。因此，研究计算圆周率的科学方法，仍然要给人们继续进行艰苦的探索。
张衡
魏晋之际杰出的数学家刘徽，在计算圆周率方面做出了突出的贡献。刘徽在公元263年注释古书《九章算术》，并撰写《重差》一书。《重差》一书在唐朝称为《海岛算经》。在为《九章算术》作注时，刘徽正确地指出，“周三径一”不是圆周率的值，实际上是圆内接正六边形周长和直径的比值。用这样的圆周率计算圆面积，算出的不是圆面积，而是圆内接正十二边形的面积。刘徽发现，当圆内接正多边形的边数增加时，多边形的周长就越来越逼近圆周长。这样的发现启发他创立了割圆术，为计算圆周率和圆面积建立了相当严密的理论和完善的算法。
刘徽割圆术的主要内容和根据是：
（1）圆内接正六边形每边长等于半径。
（2）根据勾股定理，从圆内接正n边形的每边长，可以求出圆内接正2n边形每边的长。
（3）从圆内接正n边形每边的长，可以直接求出圆内接正2n边形的面积。
（4）圆面积S满足不等式
S2n＜S＜S2n＋（S2n－Sn）
S2n是圆内接正2n边形的面积，Sn是圆内接正n边形的面积。
（5）刘徽认识到：“割之弥细，所失弥小，割之又割，以至于不可割，则与圆合体而无所失矣。”这就萌发了极限的思想，多边形边数无限增加时，它周长的极限就是圆的周长，它面积的极限就是圆面积。
刘徽从圆内接正六边形算起，边数逐步加倍，相继算出内接正十二边形，正二十四边形，直至正九十六边形的每边长，并求出正一百九十二边形面积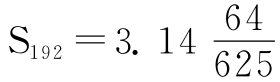
。这相当于求得π＝3.14124。在实际计算中，他采用了π＝3.14＝157/50。刘徽又继续求下去，直求出圆内接正三千零七十二边形的面积，验证了前面的结果，并且得出了更精确的圆周率值π＝3927/1250＝3.1416。
刘徽割圆术的创立，从理论上为计算圆周率探索出科学的方法，圆周率的计算，再不是用物理实体进行模拟测量后而得出的结果，因而不仅避免了测量误差，而且使其有了真正数学意义。他的计算在数学史上占有十分重要的地位。这种方法只用圆内接正多边形面积而不需计算外切正多边形，在程序上要简便一些。比起古希腊阿基米德的算法，刘徽的方法是事半功倍的。
到了南北朝时期，中国出现了一位杰出的数学家，他的名字叫祖冲之。
公元429年，祖冲之生在范阳遒县，即现在的河北省涞水县北。他生长在研究天文、历法的世家，从小接触大量有关文献和资料，并形成严谨的治学风格。他博访前故，远嵇昔典，搜练古今，博采深奥，在掌握大量已有知识的同时，坚持实际考察验证，亲身进行精密测量和细致计算，既继承了前人的成就，又纠正了以往的错误，促进了中国数学和天文学的发展，把中国的数学和天文学推进到一个新的高度。
祖冲之
祖冲之在数学上的巨大贡献是对圆周率的精确计算。他利用刘徽的割圆术，在小数还处在萌芽的时代，设圆的直径为1亿丈，以惊人的勇气和毅力，用简陋的算筹完成了大量极其复杂的计算，精确地求出圆周率π的值为：
3.1415926＜π＜3.1415927
这个计算把π值推算到小数点后7位，取得极为准确的结果，在当时乃至于以后的1000年中都是相当先进的。直到15世纪，阿拉伯数学家阿尔·卡西和16世纪法国的维叶特才又把π值向更为精确的数值推进了一步。
祖冲之还确定了两个分数形式的π的近似值，它们是：
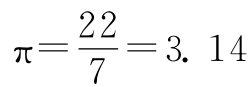这个结果称为“约率”；
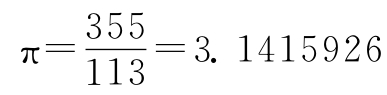这个结果称为“密率”。
我们知道，π是无理数，也就是不能用分数形式来表达的一种数。我们只能用分数来近似地表示它，越来越精确地逼近它。约率和密率就是用分数来逼近π值的两个结果。其中密率是祖冲之独立提出和首创的，密率的近似程度也是相当高的，1000年后才由德国的奥托和荷兰的安托尼兹重新提到。现在，圆周率的这一结果被人们称为“祖率”，祖冲之也被列入世界文化名人。近年来，人类对月球上的环形山加以命名，大多取文化名人的名字来命名，其中一座就被冠以祖冲之的名字。
祖冲之是无愧于文化名人之称的。因为，要把π值准确计算到小数点后7位，需要求出圆内接正12288边形的边长和24576边形的面积。这是一项非常艰难繁杂的工作，只有纯熟的技巧，深厚的理论，坚忍不拔的毅力，才能取得这样的成就。有些人以为，只要有天才的头脑就可以取得杰出的成就。殊不知天才的头脑只是成功的一半，另一半是由踏实的精神和不懈的努力来完成的。还是爱因斯坦说得好：成功就是百分之一的天才头脑加上百分之九十九的汗水。
明安图
祖冲之以后，一千年中圆周率的计算没有什么突破，一直到17世纪，近代数学发展以后才出现了以级数形式表达的π值计算公式。其中有大科学家牛顿发现的以二项展开式表示的π值计算公式，这个公式在清初传入中国，但没有公式的证明。这给中国数学家掌握和运用公式带来一定困难。当时的蒙古族数学家明安图写了一部《割圆密率捷法》的书，在书中完整地给出了π的无穷级数表示公式的证明，为用解析方法研究三角函数和圆周率开辟了新的途径。
为了证明π值表示式，明安图花费了半生心血，不仅圆满地解决了九个公式的证明，还推导出展开三角函数和反三角函数的新公式。明安图所用的是相似三角形对应边成比例的原理，用折线逼近圆弧，从折线和弦的关系导出弧和弦的关系。这样的方法，是中西结合，将割圆和比例联在一起的方法，把三角函数和圆周率研究提高到一个新的水平。
在古代割圆术中，对直线曲线关系的转化，人们的认识表现在用圆内接正多边形逼近圆周。而明安图指出：弓形中的弧是曲线，弦是直线，曲线和直线总是有区别的，不能等同。但弧和弦的关系不是无法解决的。当把某段弧长等分十分精细，以至于无穷，就可以把弧和弦统一起来，而得出彼此相求的关系。这样的认识，超出了圆内接正多边形的范围，也超出了仅仅求圆周长的范围，讨论任意长度弦和对应弧之间的关系，这是一种新的认识，是对直曲关系认识的一大进步。应当说，它突破了直就是直，曲就是曲的形而上学机械模式，进入了直曲关系的辩证认识。这不仅是数学上的进步，而且是人类哲学思维的进步。
从明安图的成就可以看出，这一时期的中国数学家，已经有了某些微积分思想萌芽。虽然中国数学没能按照自己的道路进展到这一阶段，但数学家们的贡献还是为以后数学的近代化发展打下了重要的思想基础。
书本上的知识而外，尚须从生活的人生中获得知识。
——茅盾
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
