逻辑思维的基本形式

第二节　逻辑思维的基本形式

概念、判断和推理是逻辑思维的基本形式。

一、数学概念

概念是反映研究对象的本质属性的一种思维形式，是人们主观意识对客观事物本质属性的能动反映，是一种科学认识方法。在逻辑学中，概念是思维形式的最基本组成单位，是构成判断和推理的要素。

数学概念是反映客观事物关于空间形式和数量关系方面的本质属性的思维形式。

1.数学概念的形成和特性

概念的形成是以实践为基础的。人们为了认识事物，掌握事物的规律，把握事物的本质，首先把某一类事物的本质属性及其非本质属性区别开来，然后把非本质属性撇开，将本质属性抽象出来，再运用适当的词语给予表达，从而形成概念。因此，概念的形成一般经过从客观事物到主观意识的认识过程，这个过程按照认识发展顺序就是感觉——知觉——表象——概念，其中感觉、知觉、表象（观念）属于感性认识，由表象到概念属于理性认识。概念的实质是一种思维形式，而思维则是人为的一种特殊的心理现象，是人脑对客观事物的能动的反映，是主观对客观事物的本质属性内在联系的一种概括、间接反映过程。

数学概念的形成一般都遵循由客观到主观的认识过程，初等数学中许多概念都是这样形成的。例如，人类先从感觉太阳和月亮满月时的外形开始，经过长期观察，慢慢地形成圆的观念，为了制造类似于圆的工具和器皿，促使对圆的本质属性的进一步理解，最后经过抽象概括，懂得了圆周上的点与圆心的距离保持不变的关系，从而得出了平面几何中圆的定义。

随着数学抽象程度的提高，数学概念的形成主要在于数学自身内部的矛盾运动。表现为纯逻辑的导出和内部的多级抽象，如虚数的产生来源于一元三次方程的求解；“群”概念的产生来源于高次方程根的表达形式问题的研究，等等，这些概念如“四元数”“群”“模”“范畴”“纤维丛”等，都超出我们现实生活所给予的表象，其抽象程度为一般人所难以理解和接受，然而由它们建立起来的理论在实践中有着广泛的应用。真正的数学概念的形成和确立，必须受客观的检验，不是人们主观任意臆造的“思想产物”，而是有其客观背景的。这如同微积分的概念，萌芽于古希腊时期，只是到了16世纪之后，技术的发展、微积分理论有了实际应用，这个概念才完全确立。

由于概念的产生是以感性认识为基础的，所以概念具有直观性。另外概念是借助于分析、综合、抽象、概括等方法，能动地反映各类事物对象所固有的一般的本质属性。因此，概念具有普遍性和抽象性。

概念的形成需要一个历史过程，随着事物的变化，概念自身也是发展变化的。

一些概念在事物的变化和发展过程中，反映对象的本质属性并没有发生根本变化，但是随着人类认识的发展，对概念的认识变得丰富、深刻。人类建立起来的理论不断完善、科学技术不断进步，事物的本质被揭示的可能性越大。这样，反映事物本质属性的概念随之而发展，因此，概念具有发展性。

上述特性在数学概念中有着充分体现。如平面几何和立体几何中的图形就有明显的直观性。但由于数学具有高度抽象性，所以数学概念的普遍性和抽象性较强，而直观性较弱，例如函数中最熟悉的二次函数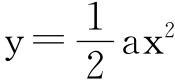，它是自由落体运动（高度与时间）、匀加速运动（距离与时间）、机械能（动能与速度）和热电学（热量与电流强度）等多种现象中变量之间关系的抽象概括。这就充分体现数学概念的普遍性和抽象性。

数学概念更突出地表现为它的发展性。数学中有不少概念，特别是较原始的概念，在揭示它的本质过程中，经历漫长的历史过程。有些概念经过几百年，甚至上千年，才能正确揭示其本质，如自然数概念，从人类认识数开始，直至集合论的建立之后，才由意大利数学家皮亚诺于1889年用公理化形式给出了它的精确定义。又如函数概念的发展，经过几次扩充、深化，才到达今天现代数学中深刻揭示其本质的关系定义。其发展过程大致经历如下几个阶段：开始，函数是幂x，x²，x³…的同义词，由17世纪莱伯尼兹首先给出，到18世纪，函数被理解为变量x与常量构成的任一表达式，并由欧拉给出函数f（x）的记号，后来随着运算的多样化，新的函数表达式的出现，特别是傅里叶证明了“由不连续的线段给出的函数能用一个三角函数式来表示”，打破了对函数概念的认识的传统观念，这个时期由柯西给出函数的定义为“若对于x的每一个值，都有确定的y值与之对应，则称y为x的函数”。这个定义较深刻地反映函数概念的本质，但当时对于“对应”的理解还不够深刻，直至一些更抽象的函数的出现，如狄里赫利构造的狄里赫利函数，使人们认识到函数的本质在于对应法则的存在，而不管其对应方式如何，或是否用解析式表示，这样，人们对函数概念的认识有了质的飞跃。至今现代数学，函数概念发展到由揭示对应关系更本质的映射来定义。并在现今的教科书得到反映。函数概念的本质逐步为中学生所认识。

2.数学概念的作用

科学概念的作用在于它的基础性和开拓性。一门科学的理论体系总是通过一系列概念的制定来总结和概括该门科学认识的成果的。因而科学理论体系即是科学概念体系。

一些科学的基本概念的形成，标志着相应的学科或理论体系的诞生。如“点”“线”“面”等，这些形的概念的提出，为欧几里得几何学创立奠定了基础。在科学的发展过程中，一个新概念的引入，往往标志着科学史上新成就的产生，而重要科学概念的形成，甚至具有划时代的意义。如“群”概念的诞生，具有划时代意义，它标志着代数学由传统代数迈向近世代数。“集合”概念的建立，使它成为整个数学的基础。因此，人们称“集合”和“群”的概念“是构成数学基础的主要思想”，“它们使纯数学和应用数学成为像今天这样发达和严密的最大源泉”。

数学概念的诞生，往往伴随着数学思想方法的诞生，如“变数”概念的诞生，促进了数和形结合方法，开创了用代数方法和从运动的观点研究几何图形和数量关系的局面，从而，诞生了解析几何，使数学进入辩证法的领域。正如恩格斯所说：“数学中的转折点是笛卡儿的变数。有了变数，运动进入了数学，有了变数，辩证法进入了数学，有了变数，微分和积分也就立刻成为必要的了……”

由于概念的形成需要积累丰富经验，需要对事物进行反复的观察、试验和理论上的探讨。在对事物的本质属性认识不清的情况下，有时会导致不正确的概念的产生，而且这样的概念会阻碍人类认识的深入和发展，在科学史上，这样的例子是不乏的，例如化学史上的“燃素”概念。它是德国医学家和化学家施塔尔在1703年提出的，他认为，“燃素”是一切可燃物质的根本要素，一切与燃烧有关的化学变化都是物体吸收和释放“燃素”的过程。这个错误的概念，曾将近100年之久阻碍人们对燃烧的本质的认识。在1774年，普利斯特列和舍勒分别析出了氧气，但不知道析出的是什么。他们只发现，当一种物体与这种气体燃烧时，这种气体就消失，后来，他们把这样的发现告诉了拉瓦锡，拉瓦锡根据实验事实重新研究了“燃素”的化学学说，终于发现这种气体是一种新的化学元素——氧。物质燃烧时，不是“燃素”分离，而是一种氧化过程。从而纠正了“燃素”概念的说法，使化学获得新的发展。

在数学史上“万物皆数”的说法是古希腊毕达哥拉斯学派提出的一种说法，他们认为“数”的形式就是（其中m，n为正整数），这个概念一直障碍数学的发展。直至他的门徒希帕索斯发现了无理数时才冲破了这个障碍，使数学得到发展。

3.数学概念的内涵与外延

概念是反映客观事物的本质属性的思维形式，因此，任一概念都反映着某一对象的本质属性。即反映客观内容的特征。另一方面通过概念反映的属性去称谓具有该属性的对象，即反映所研究的对象，这两个方面分别构成概念的内涵和外延，任一概念都是由概念的内涵和外延组成。

概念的内涵是一个概念所反映的对象的本质属性。它是概念在质方面的反映，说明概念所反映的事物的本质。

概念的外延是一个概念所反映的全部对象，它是概念在量方向的反映，说明概念所反映的事物的范围。

例如：“圆”这个概念的内涵是：“平面内，到定点的距离等于定长的点的集合”，它的外延是“一切由‘圆’组成的图形”。

虽然概念的内涵是指客观事物的本质属性，但是内涵是作为人们主观对客观事物的认识一种反映，是人们认识的结果。而客观事物的特有属性或本质属性是客观存在的，是作为认识的对象。因此，严格地说，两者之间是有区别的，只有当内涵真正地揭示所研究对象的本质属性时，它们才完全一致。

人类对客观事物的认识是不断发展的，概念的内涵也是不断发展的，随着概念的发展，内涵反映本质属性更精确，更深刻，更全面。人们在认识过程建立的错误概念逐步地被正确的概念所纠正。科学不断向前发展。

概念的内涵和外延是相互联系的。概念的内涵严格地确定着概念的外延。反之概念的外延也完全确定着概念的内涵。当概念的内涵发生变化时，概念的外延也随之变化，反过来也是一样。它们两者之间的依赖关系，遵循着反变关系（也称反变律），即当概念的外延缩小，内涵就增加，反之，外延扩大，内涵就减少。

根据反变关系，我们可以通过增加概念的内涵来缩小概念的外延以实现对新概念的认识。如果平行四边形的内涵增加“有一个角是直角”这个属性，就得到矩形的概念，这种认识概念的逻辑方法称为概念的限定，反之可以通过减少概念的内涵来扩大概念的外延，这种逻辑方法称为概念的概括。

运用概念的限定和概括的逻辑方法可以较好地形成概念系统和比较概念的异同，以及掌握概念属性，它常用于对某知识系统的整理。

4.数学概念间的关系

事物是相互联系的，概念也是相互联系的，逻辑方法上只研究概念间的外延关系，依据两个概念的外延之间是否有公共部分或公共部分的多少，来研究其关系，通常分为同一、从属、交叉、对立、矛盾等关系。前三者属相容关系，后两者属不相容关系。

将概念的外延视为集合，则它们的关系用韦恩图表示如下。

韦恩图

依图可知：

（1）相容关系

两个概念的外延至少有一部分相同，则称这两个概念的关系为相容关系。相容关系中，又分为同一关系、从属关系和交叉关系。

①同一关系：概念A和概念B的外延完全相同，则称这两个概念的关系为同一关系，即A＝B。

②从属关系：概念B的外延包含于概念A的外延，且仅为其中一部分，则称这两个概念的关系为从属关系，其中A为B的属概念，B为A的种概念。

③交叉关系：概念A的外延和概念B的外延有且仅有一部分相同，则称这两个概念的关系为交叉关系。

（2）不相容关系

两个概念的外延没有公共部分，则称这两个概念的关系为不相容关系。不相容关系中，又分为对立关系和矛盾关系。

①对立关系：属概念C的两个种概念A、B，若A、B的外延没有公共部分，且它们外延之和真包含于C的外延，则称A、B这两个概念为对立关系。

②矛盾关系：属概念C的两个种概念A、B，若A、B的外延没有公共部分，且它的外延之和恰等于C的外延，则称A、B这两个概念的关系为矛盾关系。

在同一体系中，弄清概念间的关系是十分重要的。如：概念A：等腰三角形底边上的高；概念B：等腰三角形底边上的中线。概念A与B的关系是同一关系。故具有A的性质，必具有B的性质，反之亦然。同一关系是实现由概念A性质与概念B性质之间相互转化的理论保证。

5.数学概念的定义

概念是思维的一种形式，要将思维的结果表现出来，进行交流、传递，必须运用词语或符号。在逻辑学上，将这种表现方法称之为给概念下定义，下定义就是用精练的语言、简明的方式，将概念的内涵或外延指出的方法，简言之，定义是揭示概念内涵的逻辑方法。

（1）定义的作用

一般地，揭示概念内涵的定义具有两方面的作用，这就是：每个定义都指出了，第一，具有定义揭示的性质的对象一定属于定义表示概念所反映的对象（判别性），第二，定义所反映的对象必须具有定义揭示概念的本质属性（性质性）。

如“圆”的定义表示了，平面上到定点等距的点共圆（判断平面上的点共圆）和圆上的点到圆心等距（圆的性质）。

（2）定义的组成

定义由被定义概念、联结项和已定义概念组成。

（3）概念定义的方式

①属加种差定义

方法：由被定义概念最邻近的属与被定义概念在属中区别于其他种的特性联合组成。

公式：属＋种差＝被定义概念

②发生性定义

方法：由被定义概念最邻近的属与被定义概念的对象形成的特征联合组成。

发生定义是属加种差定义的一种特殊情形。

③关系性定义

方法：由被定义概念最邻近的属与被定义概念在属中与其他对象之间关系联合组成。

关系定义也是属加种差的特殊情形。

④外延性定义

方法：直接指明被定义概念的外延。

⑤归纳定义

方法：对于与自然数有关的被定义概念，用递归的方式给出。

⑥公理化定义

用公理化的形式给出的定义形式。

⑦原始概念不加定义

数学是一个严密的逻辑体系，它必须建立在一些基础性的概念之上，这些概念是不直接加以定义的。其本质属性通过满足某些公理来隐含，或作一种公理性的默认，如几何学中的“点”“直线”“平面”等概念。

在同一体系中，概念与它的定义是不可分的。值得注意的是，概念是一种思维形式，定义是一种词语（名词）或符号的表述，两者之间是有差别的。不是所有的概念都能给出定义。如“集合”“对应”“点”“直线”“平面”等概念是一种理想化抽象思维形式，没有给出定义。

一个概念，从不同角度去揭示其本质属性会产生不同的定义，如自然数的定义有基数理论的定义——任何非空有限集合的基数称为自然数，也有序数理论的Peano给出的公理化定义。如矩形定义为“有一个角是直角的平行四边形叫做矩形”。而“对角线相等的平行四边形是矩形”作为判别定理。

在严格的科学数学体系中，一个概念只能有一个定义，如果给出两个定义，必须证明其等价，但作为教育科目的数学，由于考虑学生的认识水平和年龄生理的特点，在某一个系统中，同一概念可以有两个不同定义，如函数的定义，初中教材与高中教材给出的定义，表达形式不一样，但两者本质是等价的，但也有一些概念的两个定义不等价，如角的定义，在初中平面几何中，定义为：有公共端点的两条射线组成的图形叫做角。另外又给出，由一条射线绕着它的端点旋转而成的图形也叫做角，显然这两个定义是不等价的，因为前者不包含周角，而后者包含周角。

（4）定义的要求

为使在同一体系中，准确地揭示概念内涵界定概念的外延，下定义必须遵守下列要求：

①定义必须相称；

②定义必须简明；

③定义不能循环：

④定义一般不用否定语形式。

定义必须相称是指，被定义概念外延与使用的已知定义概念外延相同不能过宽或过窄，如“有一组对边平行的四边形是梯形”（定义过宽）；“开不尽的有理数的方根叫做无理数（定义过窄）。

定义必须简明是指下定义的词语必须简明准确，无多余的条件。如“有两条边相等或两个角相等的三角形是等腰三角形”。定义中“或两个角相等”是多余的条件，应删去。

定义不能循环是指不能直接或间接地使用被定义概念来定义被定义概念。如不能将“相互垂直的两条直线所成的角叫做直角”作为定义，因为两条直线相互垂直的定义是“两条直线相交成直角，那么这两条直线互相垂直”。

定义一般不用否定语是指在能够确切揭示概念内涵的对象，不用否定语来下定义。这样更有利于研究和建立数学系统，如使用“无理数不是有理数”作为定义，则不能较好的揭示无理数的本质属性。有些概念，其本质属性难以揭示，也只好用否定语来定义，如“平面内不相交的两条直线叫做平行线”。

6.数学概念的划分

概念的内涵借助于定义来揭示，那么概念的外延借助于哪种方法来揭示呢？前面讲述的概念间的关系是揭示外延的一种方法，此外还有借助于概念的划分来揭示概念外延的方法。

概念的划分是把一个属概念，按一定标准分为若干个不相容的种概念的逻辑方法。

划分是一种科学的分类，与通常将某一事物分成若干种情况的说法，在意义上有较大差别。

如学校在职人员分为干部、职员、工人、教师、技术员、教学辅助员、实验员、医生等等，这种分法不是划分。

逻辑学上的划分是一种专有名词。划分必须按一定标准进行的。任何划分包含三部分，它们是划分的母项（属概念）、划分的子项（各个种概念）以及划分的标准。

划分必须遵守一定的原则（要求）：①划分必须按照同一标准（定义所规定）；②划分的各子项间必须是不相容关系（定义所规定）；③划分必须相称，即划分的子项的外延之和必须等于被划分的属概念的外延；④划分不能越级，而被划分的属概念必须是划分的各子概念的最邻近的属概念。

这些要求有着不同的作用，要求①是保证划分的一致性。不能混乱；要求②和③是保证划分“不漏”“不重”；要求④是保证划分层次分明、清晰、合理。

例如，划分：

不符合要求①和②，划分中没有同一标准，且各子项关系不是不相容关系。

又如划分：

不符合要求③，其中只有两边相等的三角形被漏掉。

又如划分：

是不正确的，整式也就是多项式，这划分不符合要求②，多项式包含了单项式。即多项式与单项式有重复部分。

值得注意的是，在计算问题或讨论问题分单项式和多项式来运算和讨论只是一种方便于学生接受的做法。

又如划分：

不符合要求④，直角梯形最邻近的属是梯形，而不是四边形，按划分的要求，四边形应划分为：

这样的划分是按照标准“四边形的每组对边的平行关系”，其中没有一组对边平行为一类，只有一组对边平行为一类，有两组对边平行为一类，共三类，故划分为3个子项。

科学的划分具有两方面的作用。

（1）运用划分（分类）对各类进行讨论，达到解决问题的简化和深入的目的。

在数学中，分类讨论是一种常用的方法，它的理论基础是划分。只有正确划分，分类讨论才有保证，否则讨论会产生混乱。分类讨论，可以把解决问题的难点分散，各个击破，或者化无限为有限，实现问题的转化。

（2）运用概念分类，能清晰地构成概念系统，纲举目张，便于理解和复习整理。

如将数系划分为：

二、数学的判断

1.判断和命题

判断同概念一样也是思维的一种形式，它反映了概念与概念间的联系。判断表达人们对思维对象具有某种属性或不具有某种属性的断定。

判断是对思维对象有所断定的思维形式。

判断必须通过语言或符号来表达与用词语表达概念不同，判断的表达形式是语句。我们将表达判断的语句叫做命题。

命题是对思维对象作出肯定或否定的语句。数学命题是表达关于数学对象的判断的语句。

例如：

①两底角相等的三角形是等腰三角形；

②一个公式不是代数数；

③3≥2。

这3个语句都是判断，它们都表达了对思维对象的性质或关系作出了肯定或否定。

命题是一种特殊表达形式的语句，“有所断定”是判断的基本特征，无所断定的语句不是判断。如“4是素数吗？”不是判断，即不是命题，因为它既没有肯定什么，也没有否定什么。

命题具有真、假意义。如“凡直角都相等”是真的，“正三角形是中心对称图形”是假的，因此可知，命题是具有真假意义的语句，具有真意义的命题称为真命题，反之为假命题。

如同概念与定义一样，判断与命题是有差别的，判断是思维形式，命题是表达的语句，但当判断用语句表达时，判断也就是命题了，因此，研究判断问题与研究命题相同，两者不作区别。

2.判断的种类

在逻辑学中，判断可按不同的标准进行分类。

按判断的量分类，有全称判断，特称判断。

按判断的质分类，有肯定判断，否定判断。

按判断的关系分类，有直言判断，假言判断，选言判断。

判断的分类

按质与量来分，共有4类，见下图：

图中阴影部分表示判定部分。

特称判断的特例就是对单个对象作出判断，称为单称判断。逻辑形式是这个S是P，或这个S不是P。例如x＝2是方程x²－2x＝0的解，x＝3不是方程x²－2x＝0的解。

按关系分类，判断有三类：

直言判断：不加条件地直接断定思维对象具有或不具有某种属性的判断。

例如：

（1）正多面体只有5种。

（2）两点间的距离线段最短。

这两个判断是直言判断。

假言判断：有条件地断定某对象的某种属性或关系存在情况的判断。

逻辑形式：

①若p则q（或如果p，那么q）；

②当且仅当p则q。

例如：

（1）如果a＋b＝1，那么a，b中至少有一个不少于。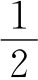

（2）若△ABC中，∠C＝90°，则AB²＝AC²＋BC²。

（3）一元二次方程ax²＋bx＋c＝0，有实数根，当且仅当判别式△≥O。

这3个判断是假言判断。

选言判断：断定某对象的若干个属性或关系中至少有一存在的情况的判断。

逻辑形式：

S或是P₁，或是P₂或是P₃；或S₁或S₂或S₃是P。

例如：

（I）空间中三个平面两两相交，有三条交线，它们的交线平行或相交于一点。

（2）如x＜2或x＞3，都有x²－5x＋6＝0。

这两判断是选言判断。

3.数学命题的真假性和作用

（1）数学命题的真假性

数学命题也是逻辑学中的命题，在逻辑学中，命题的真假性只取决于逻辑关系的真假性，而不考虑其客观实际的真假性。命题的具体内容是否符合思维对象的客观实际情况，是由思维对象的有关学科来断定的。数学命题的真实性，不但取决于逻辑形式的真实性，而且还取决于内容的真实性，只有这两方面都真实才为正确的数学判断即为数学真命题。

教学内备的真实性明显地依赖于该命题所处的数学体系例如：两个三角形三个角对应相等，则这两个三角形全等。这个命题在欧氏几何学中是假命题，但在罗氏几何学中是真命题。

数学命题的真实性更着重依赖于客观实际检验。逻辑上无矛盾是正确思维和推理的必要条件，但还不是充分条件，它依赖于推理前提的正确性。尽管“如果我们有正确的前提，并且把思维规律正确地运用于这些前提，那么结果必定与现实相符”，然而前提是否正确，数学本身是无法检验的。正如非欧几何虽然诞生了很长期间，但只有当它在相对论成功地应用，及克莱因等人在欧氏几何中构造出非欧几何的模型之后，才完全确定其理论真实性。因此数学理论是否具有客观真实性，必须由客观实践来检验。

（2）数学命题的作用

数学体系可以说是由概念、命题和推理构成。

数学命题如同数学大厦中的支架，支撑和架构着整座大厦。它连结着各个节点（数学概念）和数学基础。

数学命题揭示数学研究对象的内在联系，揭示着自然界的规律和方法。数学的研究成果和方法，主要是用数学形式给出。因此，数学命题是数学研究成果的结晶。

数学命题不但在数学自身结构和揭示外部世界的规律起着重要作用，而且对数学自身发展也起着有力的推动作用。

重要的数学命题的建立，如同重要数学概念的诞生一样具有开拓性。例如，非欧几何的诞生是建立在与欧几里得几何的第五公设相悖的公设之上罗氏几何和黎曼几何的建立标志着近代数学研究的开始，具有划时代的意义。

又如拓扑学中的四色定理，“平面地图不论多么复杂，只需用四种颜色就足以使相邻的不同区域分开”。四色问题从提出到解决经历100多年，直至1977年由美国数学家汉肯和阿佩尔借用计算机IBM360花费了1200个机器小时，检验了1482种的全部可能情况，完成了这个定理的证明。人们在寻求定理的证明过程中推动数学的发展。它的解决，正如有评论家指出，“将成为数学思想发展史上一系列新想法的起点”。

再如德国数学家希尔伯特在1900年召开的第二次国际数学代表大会提出的23个问题。这些问题揭开了20世纪数学发展的序幕，一个世纪以来，这些问题一直激励和指引着数学家们的研究。20世纪许多数学重大成就都与这些问题研究分不开，从1936年到1974年，被誉为数学界诺贝尔奖的菲尔兹国际数学奖的20名获奖者，其中至少有12人的研究工作与解决希尔伯特问题直接有关。

希尔伯特的23个问题中，“哥德巴赫猜想”与“费尔玛问题”被列为其中第8和第10个问题，这两个被誉为数学皇冠上的明珠的数论难题，吸引了不少数学家致力研究。有的数学家甚至耗费了毕生的精力，其中最突出的是德国数学家库姆尔，他几乎用了一生的时间来研究费尔玛问题。虽然他最终没有给出完满的解决，但他却提出了一整套数学理论，推动了数学的发展。法国科学院为表彰库姆尔的贡献，为他颁发了奖项。

费尔玛问题最终在20世纪末即1994年由英国维尔斯给出了严格证明，结束了历时300年之久的困扰。维尔斯的杰出成就使他荣获数学殊荣沃尔夫奖。而哥德巴赫猜想，虽然我国数学家陈景润在解决这个问题上取得最好的成就，但这个问题在18世纪提出至今仍未得到彻底解决，还正在激励着数学家为此继续攀登。

以上列举的数学命题，足以说明数学命题所起作用是巨大的，“数学问题是数学核心”，数学的发展史，也就是数学问题不断提出和解决的历史。

三、数学的推理

1.推理和推理的组成

概念与概念的联系是判断，那么概念与判断，判断与判断之间的联系是什么？那就是推理。

推理是从一个或几个已知判断推出一个新的判断的思维形式。

推理和其他思维形式一样，也要借助于语言来表达，概念借助于词语，判断借助于语句，而推理则借助于复句或句群来表达。它是由若干个命题复合而成。

任何推理都是由前提和结论两部分组成，推理的前提就是推理所依据的已知判断或概念，推理的结论就是由前提所推出的新判断。

2.推理的逻辑性和真实性

推理不是判断的无规则的罗列，“由此推出”是推理的特征。因此，推理的前提与结论之间有一定制约关系，这种关系就是逻辑关系。判断间的逻辑关系是客观规律性的反映，表现为各种逻辑基本规律和推理规则。

推理的真实性依赖于推理合乎逻辑性，合乎逻辑性包含两个方面。第一，推理内容正确反映客观事物的发展规律，即符合客观事物本身的逻辑；第二，推理过程符合思维结构的规律，即符合推理形式的发展规律。这两个方面的要求，反映了推理的内容与形式的统一性。

当前提内容真实，推理形式可靠且推理形式正确，所得的推理结论就是真实的，即为真实推理，如果缺少其中一个条件，结论就是不可靠的。

推理前提的正确性是真实推理的必要条件，只有当作为前提的判断符合客观实际，推理才有可能成为真实推理。

推理形式的可靠性同样是真实推理的必要条件，而正确运用推理形式则是获取真实推理的关键。

例如：

无理数是实数，

分数不是无理数，

所以，分数不是实数

这个推理的两个前提都为真，但推理形式不正确，故此，这个推理是一个不合乎逻辑的推理。上述推理的前提与结论之间没有必然的联系，违反了推理规则。

3.推理的种类

根据不同的标准，可以把推理划分为各种不同的类型，数学中常见的推理分类有如下几种。

①根据推理前提与结论间联系性质的不同，可将推理分为必然推理（必真推理）和或然推理（似真推理）。

必然推理是指在真实的前提下，由推理所得的结论完全正确的推理方法。

或然推理是指在真实的前提下，由推理所得的结论不一定正确的推理方法。

②根据推理的思维进程的不同，可将推理分为演绎推理、归纳推理和类比推理。

演绎推理是从一般到特殊的推理。

归纳推理是从特殊到一般的推理。

类比推理是从特殊到特殊的推理。

③根据推理前提数目的多少，可将推理分为直接推理和间接推理。

直接推理是指前提由一个判断构成的推理。

间接推理是指前提由两个或两个以上的判断构成的推理。

推理可以作多种分类，且每一类推理可以属于不同的类别，如演绎推理也是必然推理的一类。