及其在平台的实现

6.3.2　主成分回归（PCR）及其在MATLAB平台的实现

对于6.3.1节提出的问题，在求P矩阵之前，可先采用主成分分析将Y矩阵中的p个光谱变量压缩为小于样本数n的m个主成分后，再以主成分得分矩阵T为自变量替代原自变量矩阵Y，与浓度矩阵X（因变量矩阵）进行多元线性回归，由于主成分个数小于原始变量个数且主成分得分间互不相关，这样便消除了原始自变量矩阵中信息的相关和冗余现象，同时又压缩了原始矩阵中的自变量个数。因此（T^TT）可以求逆，式（6－44）可以满足。

对于其他自变量个数大于样本数的情况，如自变量间存在较强的线性相关，也可以先用主成分分析对自变量信息进行压缩后，以主成分为自变量进行回归。这种先对自变量进行主成分分析，再以主成分替代原自变量后与因变量进行多元线性回归的方法就称为主成分回归（Principal Component Regression，PCR）。

PCR的算法和过程在MATLAB下很容易实现：假设原始自变量矩阵为X_n×p，因变量构成的数据矩阵为Y_n×q。

（1）对矩阵X_n×p进行自标度化预处理获得矩阵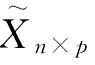，其计算公式见式（6－13）。

（2）用MATLAB中的princomp函数进行主成分分析。

（3）求累计贡献率，确定主成分个数。

（4）取前m个主成分作为主成分回归时的自变量进行多元线性回归，确定主成分回归系数矩阵B。由主成分回归模型计算得到的建模集样品的因变量矩阵采用下式求得

注意：PCR得到的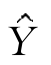通常会和实际的Y有一定差异，该差异在函数regress的返回向量Re中已经给出。

（5）根据建立的PCR模型预测未知样本的因变量。

对于k个未知或待预测样本，可根据其自变量矩阵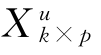，先对每个变量减去步骤（1）中的mx（注意，是减去矩阵X_n×p的列均值而不是减矩阵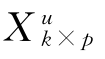的列均值），然后再除以矩阵X_n×p的对应变量的标准方差s（而不是矩阵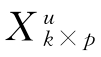的变量标准方差），求得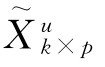，然后求其前m个主成分得分矩阵

将行数为k的单位列向量加到得分矩阵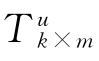的第1列，则k个未知样本的因变量为

对（1）～（5）步骤下进行主成分回归（PCR）的m文件如下

function［Mpc，pc，t，Tcrit，b，Re，R，F，Fcrit，yt，yu］＝pcr（xreg，yreg，cum，xpre，alpha）

%主成分回归建模并预测程序

%xreg为建模集自变量；yreg为建模集因变量；alpha为置信水平，取0.05或0.01

%cum为设定的累积贡献率阈值（≤1），可取0.9或0.95

%xpre为预测集的自变量矩阵（如果不做预测，xpre输入xreg即可）

%输出变量：Mpc为对应cum所确定的主成分个数，pc为前Mpc列载荷向量

%t为按照4－19计算的m个主成分的回归系数统计检验量，Tcrit为t分布的临界值

%b为m＋1个回归系数组成的列向量；Re为主成分回归模型给出的建模集样本的残差向量

%R为前m个主成分进行多元线性回归所得回归模型的复相关系数；

%F为前m个主成分进行多元线性回归所得回归模型的F统计量，Fcrit为F分布的临界值

%yu为主成分回归模型给出的未知样本的因变量值；

%yt为主成分累计贡献率向量

［ax，mx，s］＝autoscaling（xreg）；

%对建模集自变量矩阵（每一列为一个自变量）进行自标度化处理并将结果赋给矩阵ax，返回参数mx与s分别为各变量的均值与标准方差

%自编函数autoscaling见6.1.3的m文件autoscaling.m

mx，s

%显示建模集自变量xreg的均值mx及方差s

［n，p］＝size（ax）；

%将自标度化后自变量矩阵ax的行数和列数分别赋给变量n，p［U，T，lmd］＝princomp（ax）；

%对自标度化预处理后的自变量矩阵ax进行主成分分解，输出变量T为ax的主成分得分矩阵；Lmd为由大到小排列的特征值列向量（元素个数＝p）；U为p个载荷向量（列向量）构成的矩阵

yt＝cumsum（lmd）./sum（lmd）；%求每个特征值下对应的累计贡献率并赋给yt

%以下步骤确定最大主成个数

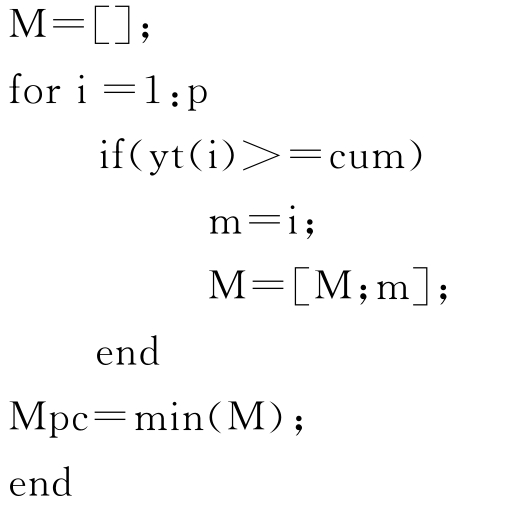
%完成最大主成个数的确定

pc＝U（：，1：Mpc）；%将前Mpc列的载荷向量赋给矩阵pc

T1＝T（：，1：Mpc）；

%将主成分得分矩阵的前m列赋给矩阵T1，T1的列数为Mpc行数为n

Tx＝［ones（n，1）T1］；

%将行数为n的单位列向量加到主成分得分矩阵T1中并赋给Tx

［b，BINT，Re，RINT，STATS］＝regress（yreg，Tx，alpha）；

%以含常数列的前Mpc个主成分得分为自变量进行多元线性回归

%b为回归系数矩阵，Re是残差向量（即回归模型的值与实际yreg的差），向量STATS含有决定系数R2及统计参数F与P值，以用于模型的统计检验。

%注意，regress函数要求yreg为列向量，因变量个数q大于1时，需要调用q次regress函数

Yc＝Tx＊b；%根据回归系数求建模集因变量矩阵Y并赋给Yc

R＝sqrt（STATS（1））；%求主成分回归模型的复相关系数R

F＝STATS（2）；%求主成分回归模型的统计检验量F比值

Fcrit＝finv（1－alpha，Mpc，n－Mpc－1）；

%求F分布在自由度n－Mpc－1下、置信度为1－alpha时的临界值

%以下根据（4－19）计算主成分回归系数（不含常数项）显著性检验的统计参数t值

cc＝inv（）；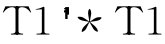

B＝b（2：Mpc＋1，：）；

t＝B./（sqrt（diag（cc））＊sqrt（sum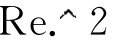（）/（n－Mpc－1）））；

%根据（4－19）计算实际计算统计量t所组成的列向量（不含常数项）

Tcrit＝tinv（（1－alpha/2），n－Mpc－1）；%获取t的临界值

%下面根据建立的主成分回归模型预测未知样本的y值

［np，pr］＝size（xpre）；%将矩阵xpre的行数和列数分别赋给np，pr

axp＝（xpre－repmat（mx，np，1））./repmat（s，np，1）；

%将预测集样的自变量减建模集对应变量的均值并除以该变量的方差（对预测样本进行自标度化预处理）

Tp＝axp＊U（：，1：Mpc）；%求预测样本的前m个主成分

yu＝［ones（np，1）Tp］＊b；%求未知样本的因变量yu

%end of pcr

例6－4　采用PCR建立例4－3中自变量与因变量之间的回归关系。

在输入原始自变量矩阵x及因变量列向量y后，在MATLAB下输入下面命令

＞＞［m，t，Tcrit，b，Re，R，F，Fcrit，yt，yu］＝pcr（x，y，0.95，x，0.05）；

屏幕显示如下结果

（为表4－5中4个自变量的均值）

（为表4－5中4个自变量的方差）

Mpc＝2（即对于阈值0.95，程序选择了2个主成分进行主成分回归建模）

F＝

119.1685（＞Fcrit＝4.1028，故前2个主成分建立的回归模型能通过统计检验）

0.3806（＜Tcrit＝2.2281，故第2个主成分的回归系数不能通过显著性检验）

打开数组b可得

则前2个主成分回归得到的回归方程如下

其中Score1、Score2为第1，2主成分得分。

打开pc矩阵可得

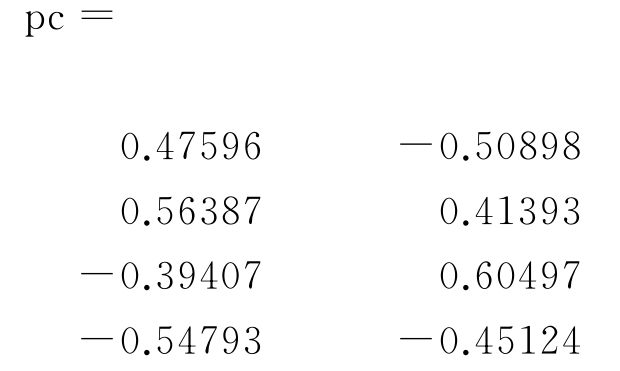
则根据式（6－17）可得

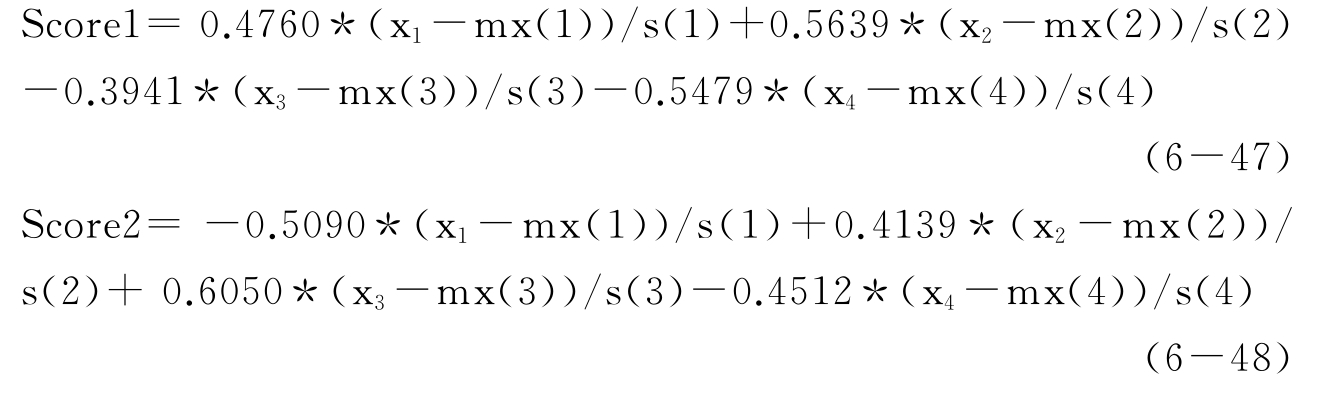
根据式（6－46）可知，第一、二主成分得分前的回归系数均为正，由式（6－47）可知第一主成分得分与表4－5中的变量x₁，x₂呈正相关、变量x₃，x₄呈负相关，所以第一主成分体现的原始变量与因变量间的关系与表4－5中实际数据间的关系一致，故第一主成分的回归系数能通过检验。但式（6－48）中呈现出的第二主成分与原始变量x₁是负相关而与原始变量x₃呈正相关，该主成分前的回归系数为正（0.289 9），因此第二主成分所反映的原始变量x₁与y是负相关关系，而原始变量x₃与y是正相关关系，这与表4－5中实际数据间的关系恰好相反。故式（6－46）中第二主成分前的回归系数未能通过统计检验。

但由于式（6－46）中第一主成分前的回归系数（9.871 9）远大于第二主成分前的回归系数（0.289 9），结合式（6－47）与式（6－48）可知，由x₁，x₂，x₃，x₄表示的回归方程（6－46）中的系数与式（6－47）中第一主成分中x₁，x₂，x₃，x₄前系数的符号相同，故式（6－46）中最终反映的y与x₁，x₂，x₃，x₄间的关系趋势与实际情况相符。

在MATLAB下输入命令

＞＞mean（abs（Re））

可得

虽然回归方程（6－46）给出的表4－5中13个样本的模型残差平均值（绝对值）为2.569 7，该值大于表4－6中所列回归方程（4－18）与式（4－21）的残差平均值，但其体现的自变量与因变量间的关系与实际情形是相符的。

例6－5　盐酸曲马多和对乙酰氨基酚复方片对于一般外科手术的术后镇痛有很好的疗效，但在该复方制剂中盐酸曲马多含量（25mg）与对乙酰氨基酚的含量（230mg）相差接近9倍，普通的紫外光光度法难以测定盐酸曲马多组分含量。为了快速确定该复方缓释制剂中盐酸曲马多和对乙酰氨基酚的释放度，本例采用主成分回归方法同时测定两组分含量。

首先要采集建模所需的实验数据，设计浓度均匀分布的19个样品见表6－9，表中第一列的数据为样品中盐酸曲马多的含量，第一行中的数据为对乙酰氨基酚的含量，表中括号内的数字代表建模及样品编号，每个样品中盐酸曲马多和对乙酰氨基酚的含量为其所在行和列的第一列和第一行中的对应数据。

表6－9　复方盐酸曲马多样品浓度设计

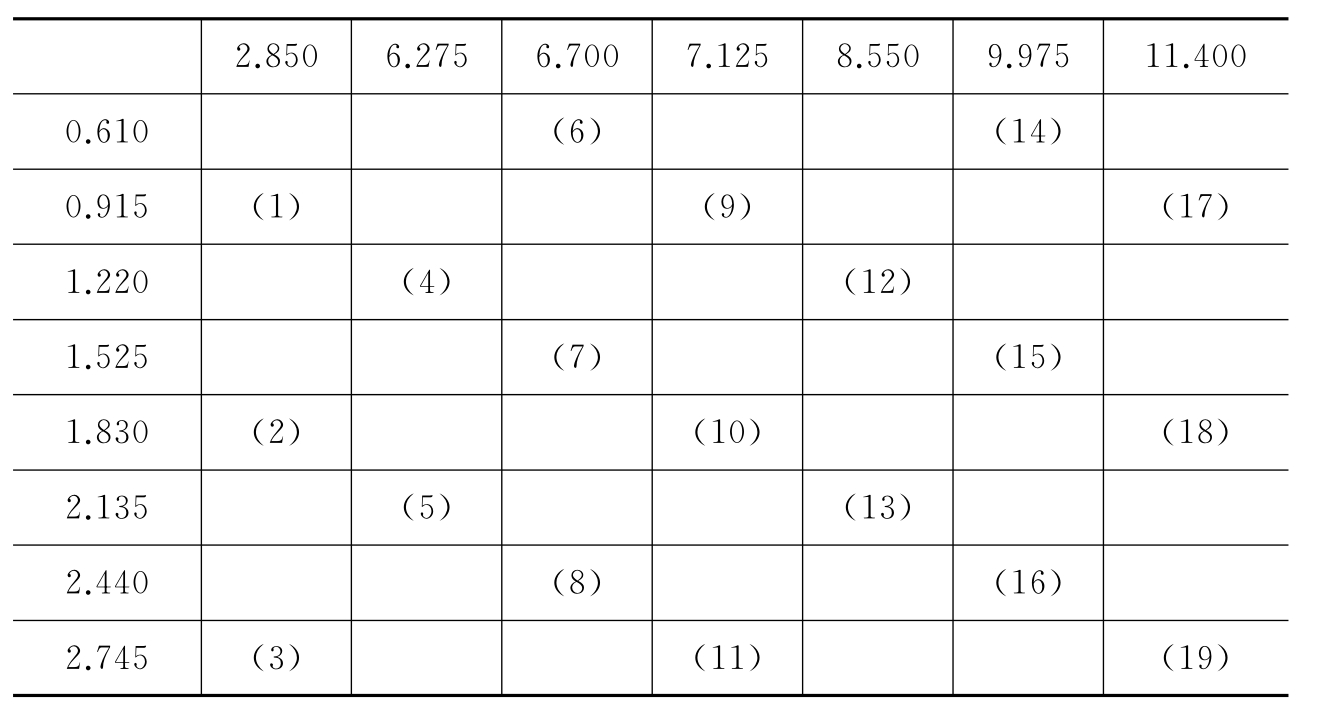
按照上表制备相应浓度的盐酸曲马多和对乙酰氨基酚复方溶液，在200～295nm波长范围内，测定其紫外吸收度如图6－13所示。

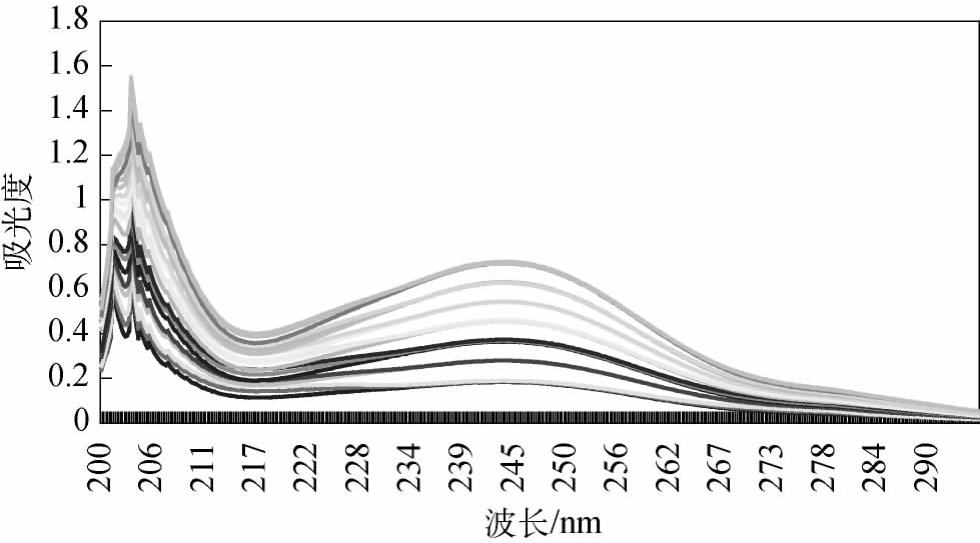
图6－13　复方盐酸曲马多样品的紫外吸收曲线

将这19个样品的紫外吸光度矩阵作为自变量数据矩阵X并按照式（6－13）进行自标度化预处理后，在MATLAB下按照步骤（2）将建模样品的吸光度矩阵进行主成分分析，按步骤（3）求得前两个主成分的累积贡献率达到了99.94%，而实际样品亦为两个成分，故取两个主成分。按照步骤（4）、（5）用前两个主成分得分矩阵和19个建模样品的浓度矩阵进行多元线性回归求得回归系数矩阵B。然后按照式(6-46)计算回归模型得到计算浓度。19个样品的实际浓度与计算浓度关系见图6-14与图6-15。

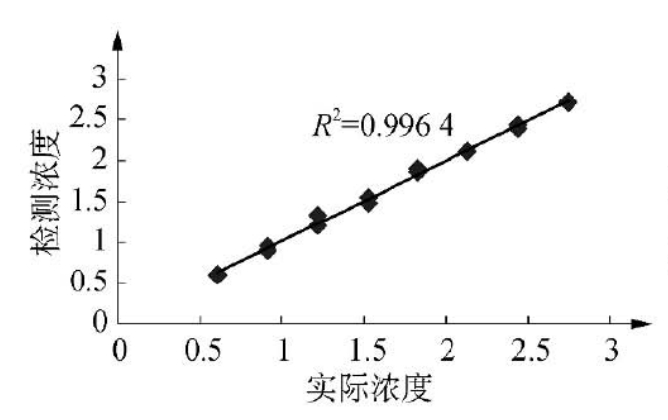
图6-14 盐酸曲马多浓度分析结果

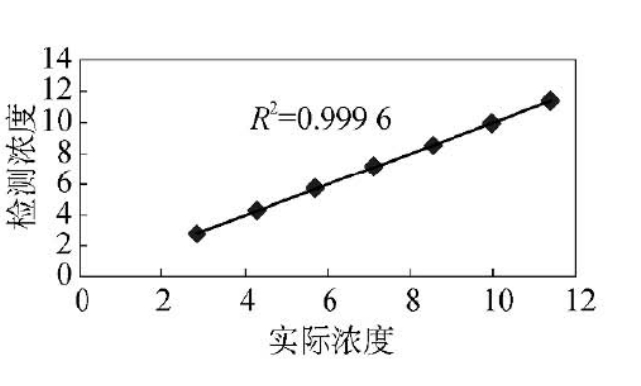
图6-15 对乙酰氨基酚浓度分析结果

图6-14与图6-15表明根据PCR所建模型回归得到的盐酸曲马多与对乙酰氨基酚浓度与实际值的线性相关系数均在0.99以上,说明该模型可以用于预测复方片的两种组分含量。