线性规划的应用范围十分广泛，但有很大的局限性，有许多实际问题还是不能处理.事实上，客观世界中的问题大部分是非线性的，线性处理大多是近似的，是在对问题作了科学的假设和简化后得到的.而在许多实际问题中，有一些是不能进行线性化处理的，否则将严重影响模型对实际问题的可指导性.因此产生了非线性规划，非线性规划比线性规划有着更强的实用性.但是非线性规划问题在计算上常常是困难的，理论上的讨论也不能像线性问题那样完整有一个成熟通用的算法，能够给出简捷的结果形式和透彻全面的结论.下面就通过几个例题来说明非线性规划与线性规划的不同之处.
例5-4 板材切割问题
某钢管零售商从钢管厂进货，将钢管按照顾客的要求切割后售出.从钢管厂进货时得到的原料钢管都是19 m.
（1）现有一个客户需要50根4 m、20根6 m和15根8 m的钢管.应如何下料最节省？
（2）零售商如果采用的不同切割模式太多，将会导致生产过程的复杂性，从而增加生产和管理成本，所以该零售商规定采用的切割模式不能超过3种.此外，客户除需要上述的三种钢管外，还需要10根5 m的钢管，应如何下料最节省？
【解题思路】
首先，应当确定哪些切割模式是可行的.所谓一个切割模式，是指按照客户需要在原料钢管上安排切割的一种组合.例如，我们可以将19 m的钢管切割成3根4 m的钢管，余料为7 m；或者将19 m的钢管切割成4 m、6 m和8 m的钢管各1根，余料为1 m.显然，可行的切割模式是很多的.
其次，应当确定哪些切割模式是合理的.通常假设一个合理的切割模式的余料不应该大于或等于客户需要钢管的最小尺寸.例如，将19 m的钢管切割成3根4 m的钢管是可行的，但余料为7 m，可以进一步将7 m的余料切割成4 m钢管（余料为3 m），或者将7 m的余料切割成6 m钢管（余料为1 m）.在这种合理性假设下，切割模式一共有7种，如表5-4所示.
表5-4 合理切割模式
问题转化为在满足客户需要的条件下，按照哪些合理的模式、切割多少根原料钢管最为节省.而所谓节省，可以有两种标准：一是切割后剩余的总余料最小，二是切割原料钢管的总根数最少.下面将对这两个目标分别讨论.
决策变量：用XI表示按照第I种模式（I=1，2，…，7）切割的原料钢管根数，显然它们应当是非负数.
决策目标：如果以切割后剩余的总余量最小为目标，由上表可得到目标函数为：minz1=3x1+x2+3x3+3x4+x5+x6+3x7.如果以切割原料钢管的总根数最少为目标，则有目标函数为：minz2=x1+x2+x3+x4+x5+x6+x7.
约束条件：为满足客户的要求，则有如下约束条件：
按照求解问题（1）的思路，可以通过枚举法首先确定哪些切割模式是可行的，但由于需求的钢管规格增加到4种，所以枚举法的工作量较大.下面介绍的整数非线性规划模型，可以同时确定切割模式和切割计划，是带有普遍性的方法.
同问题（1）类似，一个合理的切割模式的余料不应该大于或等于客户需要的钢管的最小尺寸（本题为4 m），切割计划中只使用合理的切割模式，而由于本题中参数都是整数，所以合理的切割模式的余量不能大于3 m.此外，这里仅选择总根数最小为目标进行求解.
决策变量：由于不同切割模式不能超过3种，可以用xi表示按照第i种模式（i=1，2，3）切割的原料钢管根数，显然它们应当是非负整数.设所使用的第i 种切割模式下每根原料钢管生产4 m、5 m、6 m和8 m的钢管数量分别为r1i，r2i，r3i，r4i（非负整数）.
决策目标：如果以切割原料钢管的总根数最少为目标，即目标函数表示为：min z=x1+x2+x3
约束条件：为满足客户的需求，应有如下约束条件：
每一种切割模式必须可行、合理，所以每根原料钢管的成品量不能超过19 m，也不能少于16 m（余量不能大于3 m），于是有如下约束条件：
使用建模化语言Lingo编程源程序如下所示：
Model：
sets：
number1..3：x；
modes1..4：a，b；
mode（number，modes）：r；
endsets
data：
a=50，10，20，15；
b=4，5，6，8；
enddata
min=@sum（number∶x）；
@for（modes（i）：@sum（number（j）：x（j）*r（j，i））＞=a（i））；
@for（number（i）：@sum（modes（j）：b（j）*r（i，j））＜=19）；
@for（number（i）：@sum（modes（j）：b（j）*r（i，j））＞=16）；
@sum（number∶x）＞=26；
@sum（number∶x）＜=31；
@for（number：@gin（x））；
@for（mode：@gin（r））；
End.
以Model表示程序开始，首先定义程序所需集合：在sets段中定义了三类属性的集合，x为1×3的向量，a和b为1×4的向量，r为3×4的矩阵.其中a和b为约束向量，x和r 为需要求解的决策.然后对定义的集合进行初始化，在data段中，对a和b 作了数据初始化.最后调用数学函数@sum、@gin依次输入目标函数与约束条件，最后以End表示程序的结束.而@sum（number∶x）＞=26和@sum（number∶x）＜=31给求解的答案限定了求解的范围.通过上述模型可以发现，虽然目标函数还是线性表达式，但是在约束条件中出现了两变量乘积的形式，为非线性项.因此以上模型属于非线性规划模型，应该用Lingo求解.由于篇幅所限，本书只是给出了若干使用建模化语言编程的范例.对于Lingo编程学习有兴趣的同学可以参看谢金星老师编写的《优化建模与Lindo/Lingo软件》.
按住Ctrl＋S运行，得到运行结果如下：
Local optimal solution found．
Objective value： 26.00000
Extended solver steps： 13
Total solver iterations： 509
Variable Value Reduced Cost Row Slack or Surplus Dual Price
X（1） 10.00000 1.000000 1 28.00000 -1.000000
X（2） 10.00000 1.000000 2 0.000000 0.000000
X（3） 8.000000 1.000000 3 0.000000 0.000000
A（1） 50.00000 0.000000 4 0.000000 0.000000
A（2） 10.00000 0.000000 5 1.000000 0.000000
A（3） 20.00000 0.000000 6 0.000000 0.000000
A（4） 15.00000 0.000000 7 1.000000 0.000000
B（1） 4.000000 0.000000 8 3.000000 0.000000
B（2） 5.000000 0.000000 9 3.000000 0.000000
B（3） 6.000000 0.000000 10 2.000000 0.000000
B（4） 8.000000 0.000000 11 0.000000 0.000000
R（1，1） 2.000000 0.000000 12 2.000000 0.000000
R（1，2） 1.000000 0.000000 13 3.000000 0.000000
R（1，3） 1.000000 0.000000
R（1，4） 0.000000 0.000000
R（2，1） 3.000000 0.000000
R（2，2） 0.000000 0.000000
R（2，3） 1.000000 0.000000
R（2，4） 0.000000 0.000000
R（3，1） 0.000000 0.000000
R（3，2） 0.000000 0.000000
R（3，3） 2.000000 0.000000
R（3，4） 2.000000 0.000000
上述结果显示，通过2674次迭代可以得到最优解.为满足客户需要，需要28根原材料进行切割.在第一种切割模式下，将19 m的钢管切成2根4 m钢管、1根5 m的钢管和1根6 m的钢管.在第二种切割模式下，将19 m钢管切成3根4 m钢管和1根6 m钢管.在第三种切割模式下，将19 m钢管切成2根6 m钢管和2根8 m钢管.在决策中需要将10根钢管按照第一种模式切割，10根钢管按照第二种模式切割，8种钢管按照第三种模式切割.
例5-5 储油罐的变位识别与罐容表标定——CUMCM2010
通常加油站都有若干个储存燃油的地下储油罐，并且一般都有与之配套的“油位计量管理系统”，采用流量计和油位计来测量进/出油量与罐内油位高度等数据，通过预先标定的罐容表（即罐内油位高度与储油量的对应关系）进行实时计算，以得到罐内油位高度和储油量的变化情况.
许多储油罐在使用一段时间后，由于地基变形等原因，使罐体的位置会发生纵向倾斜和横向偏转等变化（以下称为变位），从而导致罐容表发生改变.按照有关规定，需要定期对罐容表进行重新标定.图5-2是一种典型的储油罐尺寸及形状示意图，其主体为圆柱体，两端为球冠体.图5-3是其罐体纵向倾斜变位的示意图，图5-4是罐体横向偏转变位的截面示意图.
请你们用数学建模方法研究解决储油罐的变位识别与罐容表标定的问题.
对于实际储油罐，试建立罐体变位后标定罐容表的数学模型，即罐内储油量与油位高度及变位参数（纵向倾斜角度α和横向偏转角度β）之间的一般关系.请利用罐体变位后在进/出油过程中的实际检测数据（附件），根据你们所建立的数学模型确定变位参数，并给出罐体变位后油位高度间隔为10 cm的罐容表标定值.进一步利用附件中的实际检测数据来分析检验你们模型的正确性与方法的可靠性.
图5-2 储油罐正面示意图
图5-3 储油罐纵向倾斜变位后示意图
图5-4 储油罐截面示意图
【附件】 附件可以通过官方网站下载http：//mcm.edu.cn.
【解题思路】
对变位误差的讨论需要计算储油罐容量，而在其表达式的确定中，关键就是要根据储油罐变位后的几何关系，确定出误差较小且计算量不过于复杂的积分方式.本文的想法是通过建立两个模型分别对油罐容量的精确值进行的数值求解，和近似值进行符号求解，从不同角度比较验证两个模型的优劣与可靠程度，最后决定较为可信的求解方式.对容器，由于容器的形状并不如假设中的那么规则，理论值总是或多或少偏离实际的测量值，故我们需要对模型的误差做适当修正.
问题需要得出罐内储油量与油位高度及变位参数之间的一般关系.首先我们分别研究了两种变位对测量值高度和实际高度的对应关系.然后采用两种积分方法对储油罐中的油液体积进行精确求解，由于斜球冠部分积分关系比较复杂，无法算出准确的一般表达式，故采用数值积分的方法.利用附件中的储油量体积和高度及每次出入流量的对应关系，求出了罐体体积的精确值，进而通过计算机编程采用穷举法可以求得理论值与实际值离差最小的情况下的和的值.前面的求解方法虽然能求解出较精确的体积值，但无法得出一般表达式.最终通过简单的切余补缺的方式进行简化，把斜球冠的积分转化为正球冠的积分.经过上面的简化后，可以求得一般表达式，然后根据最小二乘法原理建立优化模型，可以求得和的值.
图5-5 几何关系图
储油罐的物理形状如图5-5所示，从图中可以看出储油罐主要可以分为两部分：中间的圆柱形部分和两边的球冠部分，这里我们取两边的球冠为圆球的一部分.
横向偏转角度β偏斜角对测量高度和实际高度的影响的几何关系如图5-5所示.
液面离罐底的实际垂直高度为h4，测量高度为浮油子离底面的距离为h2，这两条高线都过圆形的圆心，那么可以列如下方程：h4-R=（h2-R）cos β.
其中R为某一位置截面的半径的大小，这样就得到了h4关于h2和β的表达式.纵向倾斜角度α对测量高度的影响，分为圆柱体和球冠两种情况.对于圆柱体部分，问题（1）已经讨论过我们只需要套用模型一的结论，而对于圆冠部分以左半边球冠的体积计算为例讨论，左半边的球冠的参数关系如图5-6所示.
根据图中显示的几何关系可以得到如下关系式：
这样就得到了H关于h4和α的关系式.油液面和圆冠面在轴线平面内的交点为D，DA′⊥AO′1，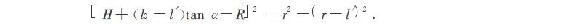
（若在左半球记为H1，右半球记为H2），由球的半径和截面圆的半径之间的关系，可得：
其中l0为圆冠高度，R为圆筒的半径，r为球冠对应圆球的半径，都已知这样得到了l′关于H和α的关系式.可以求得任意一位置l处，对应的油液的深度（记左边球冠为h′，右边球冠为h″）为：
图5-6 左半边球冠的参数关系
这样可得h关于H、l和α的关系式.每一个截面对应的整圆的半径Rl为：Rl=
.又圆形截面的高度和油液面积的关系可以使用模型一中计算椭圆的情况的计算公式，只是这时取a=b=R 的特殊情况.表达式为：
综合以上各式，可得球罐上任意一位置l′＜l＜1所对应的截面积为Sα，β，H1，l，若H1＜R-l0tan α，H1由公式得到，液面在A点以下，所以在计算球冠体积时只需要从把Sα，β，H1，l按l在l′，1区间内积分；若H1≥R-l0tan α，液面在A点以上.在计算球冠体积时除了要计算l′，1区间内的球冠体积，还需要计算最边上区间0，l′内的整圆截面的积分，这时的截面积
.那么左边球冠的体积为：
同理右边半球的体积为：
圆柱部分截面积和实际高度的关系：
那么这部分总的体积为：V=V1+V2+V3.
用Matlab编程理论上可以分别求出V1，V2和V3关于α，β，h2的表达式，但由于表达式过于复杂，迭代过程可能产生较大的误差.故采用数值积分的方法进行求解，α，β的值通过循环迭代得到某一精度下的值，迭代结果为α，β=2.23450，4.41180，这时
.
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
