对于数学建模问题，如果能够用不同的方法建立数学建模，显然最简单的方法是我们的首选，这就是所谓的工程师原则.许多初学者喜欢在比赛中采用一些启发式算法建立数学模型，如遗传算法、模拟退火算法等，但是大部分初学者并没有完全理解这些算法或者启发式算法得到的答案还不如用简单模型计算得到的答案，最后结果适得其反.本章介绍几类常用的初等数学建模方法，旨在帮助大家逐渐进入数学建模的世界.
某学院有3个系共200名学生，其中甲系100人，乙系60人，丙系40人，现要选出20名学生代表组成学生会.如果按学生人数的比例分配席位，那么甲乙丙系分别占10、6、4个席位，这当然没有什么问题（即公平）.但是若按学生人数的比例分配的席位数不是整数，就会带来一些麻烦.比如甲系103人，乙系63人，丙系34人，怎么分？表2-1按“比例”来分配20和21个席位，你认为这样分配公平吗？
表2-1 分配方案
【解题思路】
按照“比例”分配20个席位：甲、乙、丙三系分别得到10.3、6.3、3.4席，舍去小数部分后分别得到10、6、3席，剩下的1席分给“损失”最大（即小数部分最大）的丙系，于是三个系仍分别占10、6、4席.按照“比例”分配21个席位：甲、乙、丙三系分别得到10.8、6.6、3.5席，舍去小数部分后分别得到10、6、3席，剩下的2席分给“损失”最大（即小数部分最大）的甲系和乙系，于是三个系分别占11、7、3席.这样的分配是不公平的，至少对丙系而言是不公平的！因为席位增加了，而丙系得到的席位反而减少了.
通过对于问题的分析可以发现，本题需要解决这样一个问题：某校共有m个系，第i系学生数为ni（i=1，2，…，m），校学生会共设N个席位.怎样才能公平地把这些席位分配给各系？
显然，m与ni（i=1，2，…，m）应为正整数，全校学生数记为
.假设每个系至少应分得一个席位（否则把其剔除），至多分得ni（i=1，2，…，m）个席位，m≤N＜n.对于全校而言，每个席位代表的学生数为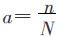
.第i系按学生数比例应分得的席位数为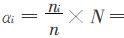
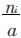.第i系实际分得的席位数为Ni，第i系每个席位代表的学生数可以表示为
.通过分析可以认为：ai越大的系损失越大，因此需要尽量照顾或者认为各系ai应该尽量接近.故可提出如下各种“公平性”标准：
标准1：要求z=max ai最小，即损失最大的系损失尽量小.
标准2：要求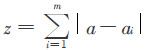
最小，即各系的损失应该尽量接近.
标准3：要求z=min ai最小，即损失最小的系损失尽量小.
标准4：要求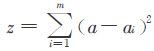
最小，即各系的损失应该尽量接近.
针对不同的标准，可以建立不同的模型.本书仅针对标准1进行建模讨论.
a i 取整后，每席代表的学生数为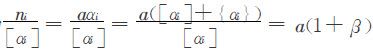
.其中，β =
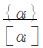，称为判别数；{αi}表示αi的小数部分.βi越大的系就越吃亏，按照标准1应该优先照顾.分配方法的算法流程如图2-1，其中
.
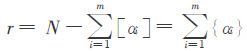图2-1 算法流程图
当N=21，n =200时，运用标准1进行如下计算，得到席位分配如表2-2所示.
表2-2 席位分配表
图2-1算法流程可以用如下整数非线性规划模型表示：
其他三种标准可以通过类似方法进行计算，本节还给出了另外一种公平席位分配方法——Q值法.首先给出公平程度定义，如表2-3所示.
表2-3 公平程度示意表
本节先就A、B两方席位分配情况加以说明.设A、B两方人数分别为p1、p2，占有席位分别为n1、n2，则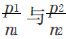
表示两方每个席位所代表的人数.显然只有当
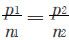时，席位分配才是公平的.但是由于人数和席位都是整数，通常两者是不等的，这时席位分配不公平.
不妨假设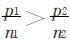
，即分配对A方是不公平的，直观的想法是用数值
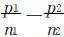表示对A的绝对不公平值，但绝对不公平值往往难以区分不公平程度.所以，绝对不公平值不是一个好的衡量指标.为了改善上述绝对标准，因此引入相对标准：
若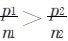
，则称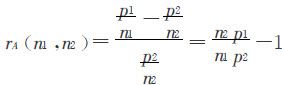
为对A的相对不公平值；若
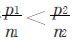，则称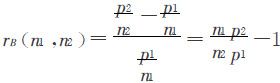
为对B的相对不公平值.建立了衡量分配不公平程度的数量指标后，制订席位分配方案的原则是使它们尽可能小.
假设A、B两方已分别占有n1和n2个席位，利用不公平值来确定，当总席位增加1席时，应该分配给A方还是B方.不失一般性，设
，即对A不公平.当再增加一个席位时，有下列三种情形：
（1）
，这表明即使A方再增加1席，仍对A不公平，所以这1席显然应分给A方；
（2）
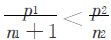，这表明A方增加1席，将对B不公平，此时对B的相对不公平值为：
；
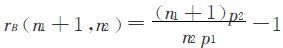（3）
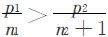，这表明B方增加1席时，将对A更不公平，此时对A的相对不公平值为：
.
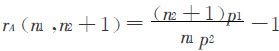按照公平分配席位的原则，即使得相对不公平值尽可能小，所以如果rB（n1+1，n2）＜rA（n1，n2+1），则这一席应给A方，反之则应给B方.根据上述确定的分配方案，可对其进行简化.注意到rB（n1+1，n2）＜rA（n1，n2+1）等价于：
并且不难证明，情形（1）的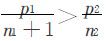
也可推得此式.于是得到结论：当上式成立时，增加的1席应分给A方，反之应分给B方.若记
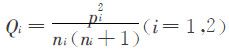，则增加的1席应分配给Q值较大的一方.这种席位分配方法称为Q值法.上述Q值法还可以推广到m方的情况：设Ai方人数为pi，已占有ni个席位，当总席位增加1席时，计算
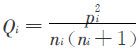（ni+1）（i=1，2，…，m），则这一席位应分配给Q值最大的一方.
下面按照Q值法对甲、乙、丙三系的21个席位重新计算.先算比例再取整，可得n1=10，n2=6，n3=3，已占取19个席位.现讨论第20和21席位归于何方，结果如表2-4所示.
表2-4 席位分配表
【思考题】
本节给出了两种不同方法的席位分配模型，请讨论哪种模型更加公平，是否存在其他方案？
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
