克莱姆法则

例1．1．2　当λ为何值时，行列式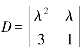的值为0？

解　因为要使λ（λ－3）＝0，须使λ＝0或λ＝3．

即知当λ＝0或λ＝3时，行列式的值为0．

思考：当D的值不为0时，λ又该如何取值呢？

例1．1．3　求解二元线性方程组

解　由于系数行列式，知该方程组有解．

再由于即得方程组的解为

用这个式子表示线性方程组的解的形式比原来更为烦琐，但这创造了多元线性方程组的解的公式及其规律性的解法，为下一步学习矩阵知识做好了准备．

与二元一次方程组类似地，对于三元一次方程组

的解，引进记号

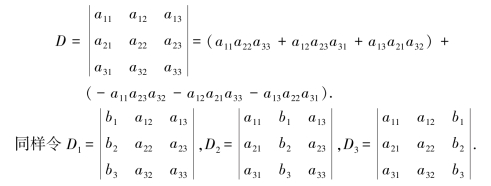
则当D≠0时，三元一次方程组的解可简洁地表示为

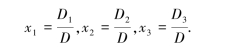
定义1．1．2　有9个数排成3行3列的数表

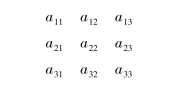
记

为三阶行列式．aij称为行列式的元素（简称元），其中i称为元素的行标，j称为列标．

可见三阶行列式仍为一个数值，这个数值可按图1．1的对角线法则计算得到．

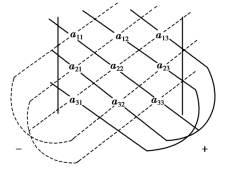
图1．1

从上图中可看出，三阶行列式是满足以下条件的6个项的代数和：从左上角到右下角的每条连线上，来自不同行不同列的三个元素的乘积，规定代数符号为正号；从右上角到左下角的每条连线上，来自不同行不同列的三个元素的乘积，规定代数符号为负号．

解　由于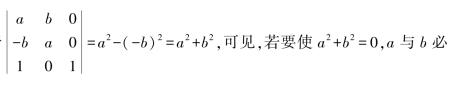须同时为0．

因此，当a＝b＝0时，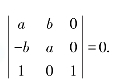

下面对三阶行列式进行整理，观察其与二阶行列式的关系．

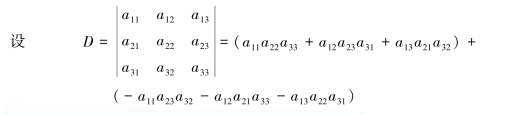
上式右端6项两两合并，提取公因式后可得下式

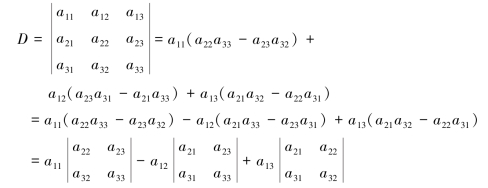
由上述结果可见，一个三阶行列式可以表示为三个二阶行列式的代数和．推广二阶、三阶行列式的定义，可以得到一般的n阶行列式的定义．

为了给出n阶行列式的计算，我们先给出余子式和代数余子式的概念．

定义1．1．3　在n阶行列式D中划去元素aij（i，j＝1，2，…，n）所在的第i行、第j列后，余下的元素按原来的次序构成的（n－1）阶行列式，称为元素aij的余子式，记为Mij；并称（－1）i＋jMij为元素aij的代数余子式，记为Aij，即Aij＝（－1）i＋jMij．

如在三阶行列式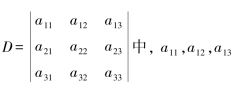的余子式和代数余子式分别为

不难写出

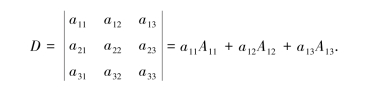
由此可以用递推法定义n阶行列式的值：

定义1．1．4　当n＝1时｜a11｜＝a11（注意这里｜a11｜不是a11的绝对值），当n≥2时，n阶行列式

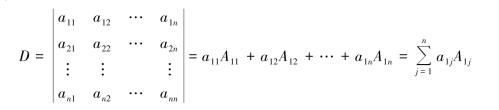
注：①通过定义1．1．4计算一个n（n＞3）阶行列式，就要计算n个n－1阶行列式，而计算一个n－1阶行列式，就要计算n－1个n－2，……如此进行下去，最后计算一个n阶行列式，就要计算n（n－1）…4个三阶行列式，计算量相当大．

②四阶以上（包含四阶）的行列式的计算不再适用对角线法则．

③行列式D的左上角到右下角连线称为D的主对角线，主对角线上元素为a11，a22，…，ann．

为了简化计算，我们需要研究行列式具有的性质，为此先计算几个特殊的n阶行列式．

由行列式定义知道，如果行列式中第一行元素除a1j以外都为零，则有

此行列式称为下三角行列式，其特点是当i＜j时aij＝0（i，j＝1，2…，n），即主对角线以上元素都为零，主对角线下方元素不全为零．

解　行列式的第一行除a11以外都为零，所以由定义得

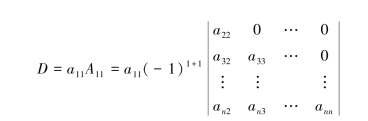
A11是n－1阶下三角行列式，则继续由定义得

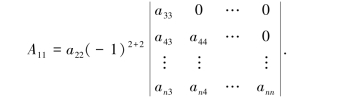
以此类推，可得

D＝a11a22…ann

即下三角行列式等于主对角线上元素之积．

特别地，主对角行列式

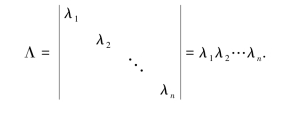
特别地，副对角行列式

∗注：n阶行列式还可以有另外一种定义方式，可以证明这两种定义是等价的，而这种新的定义需要先定义全排列及其逆序数的概念．如下：

定义1．1．5　由n个数1，2，…，n组成的一个有序数组称为这n个元素的一个n阶全排列（简称n阶排列），记为i1i2…in或j1j2…jn．

n个不同元素的所有排列的种数，通常用Pn表示．如1，2，3的所有排列为P3＝3·2·1＝6．

同理Pn＝n·（n－1）·…·3·2·1＝n！．

按数字由小到大的自然顺序排列的n阶排列1，2，…，n称为标准排列．

定义1．1．6　在n个元素的任一排列中，当某两个元素的先后次序与标准次序不同时，则称这两个数构成一个逆序．在排列i1i2…in中所有逆序的总数称为这个排列的逆序数，记为τ（i1i2…in）．

逆序数为奇数的排列称为奇排列，逆序数为偶数的排列称为偶排列．

例1．1．9　求排列3214的逆序数．

解　在排列3214中，3排在首位逆序数为0；2的前面比2大的数只有一个“3”，故逆序数为1；1的前面比1大的数有两个“3、2”，故逆序数为2；4是最大数，逆序数为0．

于是排列的逆序数为τ（3214）＝0＋1＋2＋0＝3．

注：一般求逆序数都是从一侧（左侧或右侧）依次查找计算，也可按照自然顺序查找．

定义1．1．7　n阶行列式的定义：设有n2个数，排成n行n列的数表

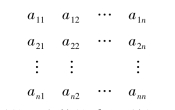
作出表中位于不同行不同列的n个数的乘积，并冠以符号（－1）τ，得到形如

（－1）τa1j1a2j2…anjn　　　　（1．1．3）

的项，其中j1j2…jn为自然数1，2，…，n的一个排列，τ为这个排列的逆序数．这样的排列共有n！个，所有这n！项的代数和

称为n阶行列式，记作

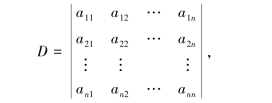
简记作det（aij）．数aij称为行列式的元素．

§1．2　行列式的性质

利用行列式的定义直接计算行列式一般很困难，行列式的阶数越高，困难越大．为了简化行列式的计算，下面来讨论行列式的性质．

首先介绍一个重要定理．由上节n阶行列式的定义知，n阶行列式可表示为第一行的元素与起对应的代数余子式的乘积之和．事实上，行列式可由任意一行（列）的元素与其对应的代数余子式的乘积之和表示．

定理1．2．1　n阶行列式等于它的任意一行（列）各元素与其代数余子式的乘积之和，即

D＝ai1Ai1＋ai2Ai2＋…＋ainAin（i＝1，2，…，n）

或

D＝a1jA1j＋a2jA2j＋…＋anjAnj（j＝1，2，…，n）．

证明略．

该定理又称为行列式按某行（列）展开定理，特别地：

推论1．2．1　如果行列式中第i行元素除aij外都为零，那么行列式等于aij与其对应的代数余子式的乘积，即

D＝aijAij．

对于n阶行列式

若把D中每一行元素换成同序数的列的元素，得新行列式：

则行列式DT称为行列式D的转置行列式，有时也用D′表示D的转置行列式．

性质1．2．1　行列式与它的转置行列式相等．

证　用数学归纳法．

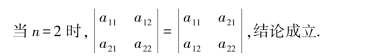
假设对n－1阶行列式结论成立．对于n阶行列式D和DT，分别按第一行和第一列展开，得

由于M1j和MT1j是n－1阶行列式，且MT1j是M1j的转置行列式，根据假设M1j＝MT1j，于是D＝DT．证毕．

例如，上三角行列式

由性质1．2．1得

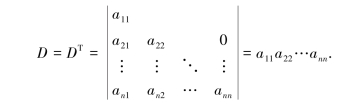
性质1．2．1表明，行列式中的行与列具有同等的地位，行列式的性质凡是对行成立的对列也同样成立，反之亦然．

性质1．2．2　互换行列式的两行（列）的元素，行列式改变符号．

证　用数学归纳法．

假设对n－1阶行列式结论成立．对于n阶行列式

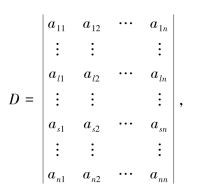
互换D中第l行和第s行的元素，得

分别将D和D1按第i行展开（i≠s，l），得

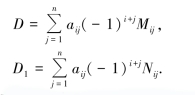
其中，Mij和Nij分别是D和D1中元素aij的余子式，且Nij是由Mij互换两行得到的n－1阶行列式，由归纳假设，Mij＝－Nij，因此D＝－D1．

证毕．

通常以ri表示行列式的第i行，以ci表示行列式的第i列．交换i，j两行，记作ri↔rj，而交换i，j两列记作ci↔cj．

推论1．2．2　如果行列式有两行（列）完全相同，则此行列式为零．

证　把完全相同的两行（列）互换，有D＝－D，故D＝0．

性质1．2．3　行列式的某一行（列）中所有的元素都乘以同一数k，等于用数k乘此行列式，即

证　将左边行列式按第i行展开即得．

证毕．

第i行（或列）乘以k，记作kri（λci）．

推论1．2．3　行列式中某一行（列）的所有元素的公因子可以提到行列式符号外面．

推论1．2．4　若行列式中有一行（列）的元素全为零，则行列式为零．推论1．2．5　若行列式中有两行（列）对应元素成比例，则行列式为零．

性质1．2．4　若行列式的某一行（列）的元素aij都可表示为两元素bij和cij之和，即aij＝bij＋cij（j＝1，2，…，n，1≤i≤n），则该行列式可分解为相应的两个行列式之和，即

其中，D1为上式右边第一个行列式，D2为上式右边第二个行列式．

证毕．

性质1．2．5　把行列式的某一行（列）的各元素乘以同一常数加到另一行（列）对应的元素上，行列式的值不变，即上式右边第一个行列式为D，第二个行列式两行成比例，由推论1．2．3知行列式为零，因此右边等于D．

证毕．

性质1．2．6是简化行列式的基本方法，若用数k乘第j行（列）加到第i行（列）上，简记为ri＋krj（ci＋kcj）．

由定理1．2．1和上述性质，可得以下定理：

定理1．2．2　行列式任一行（列）的元素与另一行（列）的对应元素的代数余子式乘积之和等于零．即

ai1Aj1＋ai2Aj2＋…＋ainAjn＝0，i≠j，或a1iA1j＋a2iA2j＋…＋aniAnj＝0，i≠j．

证　把行列式D按第j行展开，有

在式中把ajk换成aik（k＝1，…，n），可得

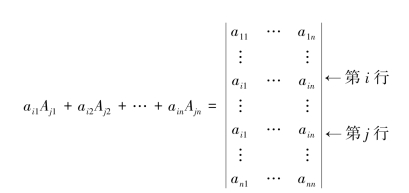
当i≠j时，上式右端行列式中有两行对应元素相同，故行列式为零，即得

ai1Aj1＋ai2Aj2＋…＋ainAjn＝0，（i≠j）．

上述证法如按列进行，可得

a1iA1j＋a2iA2j＋…＋aniAnj＝0，（i≠j）．

证毕．

综合定理1．2．1和定理1．2．2，关于代数余子式有如下重要结论：

或

其中

仿照定理1．2．2证明中所用的方法，将行列式D按第i行展开的展开式

D＝ai1Ai1＋ai2Ai2＋…＋ainAin

中，用b1，b2，…，bn依次代替ai1，ai2，…ain，可得

例1．2．1计算

解　保留a33，把第3行其余元素变为0，然后按第3行展开：

例1．2．2　设

求A11＋A12＋A13＋A14及M11＋M21＋M31＋M41的值．

解　A11＋A12＋A13＋A14＝1×A11＋1×A12＋1×A13＋1×A14

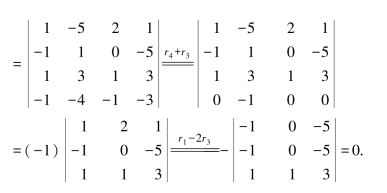
§1．3　行列式的计算

利用行列式的性质，以及行列式按行按列展开定理，可以化简行列式的计算．

例1．3．1　计算行列式

解　这是一个阶数不高的数值行列式，通常将它化为上（下）三角行列式来计算．

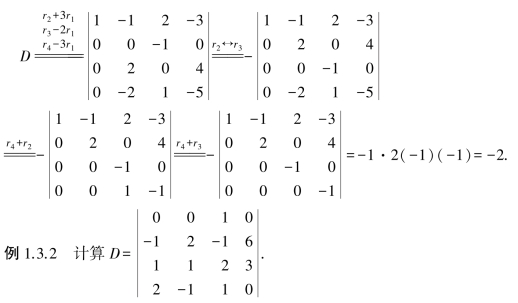
解　这是一个阶数不高的数值行列式，某行（列）里面零元很多，此时可以考虑按行（列）展开，以达到降阶简化计算的目的．

例1．3．3　计算n阶行列式

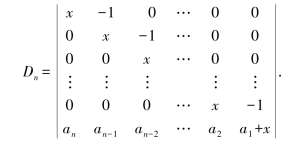
解　按第一列展开，得：

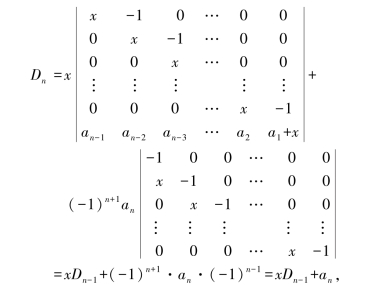
这里Dn－1与Dn有相同的结构，但阶数是n－1的行列式．

现在利用递推关系式计算结果．对此，只需反复进行代换，得：Dn＝x（xDn－2＋an－1）＋an＝xDn－2＋an－1x＋an＝x（xDn－3＋an－2）＋an－1x＋an＝…＝xn－1D1＋a2xn－2＋…＋an－2x2＋an－1x＋an．

因D1＝｜x＋a1｜＝x＋a1，故Dn＝xn＋a1xn－1＋…＋an－1x＋an．

例1．3．4　计算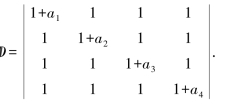

解　这个行列式主对角线元素比较复杂，而主对角线元素以外都是同一个元素，可以考虑使用加边法，加边之后的行列式与原行列式等值，容易计算．

解　观察行列式，有各行（列）4个数之和相等的特点．利用性质把第2、3、4列（行）同时加到第1列（行），提出公因子6，然后各行减去第1行，得

例1．3．6　证明范德蒙行列式：

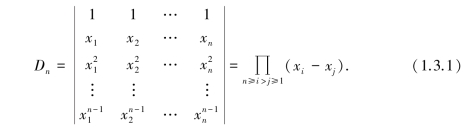
其中，记号“∏”表示全体同类因子的乘积．

证　用数学归纳法．因为

所以当n＝2时，式（1．3．1）成立．现在假设式（1．3．1）对于n－1阶范德蒙行列式成立，要证它对n阶范德蒙行列式也成立．

为此，设法把Dn降阶：从第n行开始，后行减去前行的x1倍，有

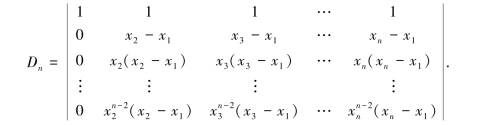
按第1列展开，并把每列的公因子（xi－x1）提出，就有

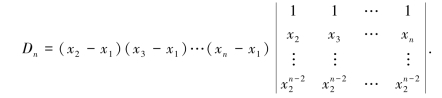
上式右端的行列式是n－1阶范德蒙行列式，按归纳法假设，它等于所有（xi－xj）因子的乘积，其中n≥i＞j≥2．故

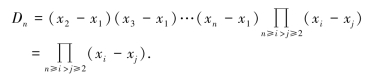
证毕．

例1．3．7　计算

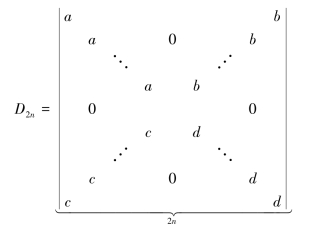
解　按第1行展开，有

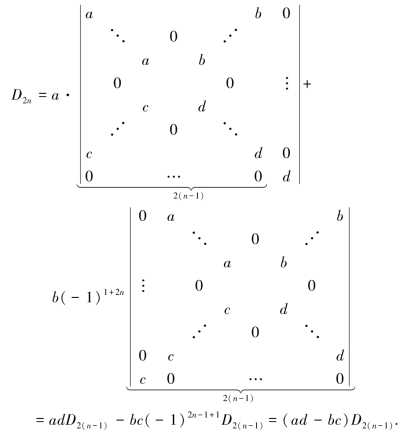
以此作为递推公式，即可得

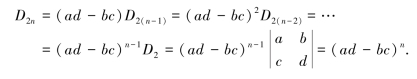
§1．4　克莱姆法则

含有n个未知数x1，x2，…，xn的n个线性方程的方程组

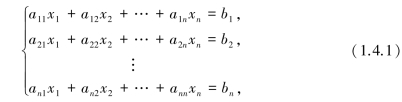
与二、三元线性方程组相类似，它的解可以用n阶行列式表示，即有

克莱姆法则　如果线性方程组（1．4．1）的系数行列式不等于零，即

那么，方程组（1．4．1）有唯一解

其中，Dj（j＝1，2，…，n）是把系数行列式D中第j列的元素用方程组右端的自由项代替后，所得到的n阶行列式，即

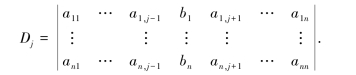
证　用D中第j列元素的代数余子式A1j，A2j，…，Anj依次乘方程组（1．4．1）的n个方程，再把它们相加，得

根据代数余子式的重要性质可知，式中xj的系数等于D，而其余xi（i≠j）的系数均为0，又等式右端即是Dj．于是

Dxj＝Dj，（j＝1，2，…，n）．　　（1．4．3）

当D≠0时，方程组（1．4．3）有唯一的一个解（1．4．2）．

由于方程组（1．4．3）是由方程组（1．4．1）经乘数与相加两种运算而得，故方程组（1．4．1）的解一定是方程组（1．4．3）的解．今方程组（1．4．3）仅有一个解（1．4．2），故方程组（1．4．1）如果有解，就只能是解（1．4．2）．

为证明解（1．4．2）是方程组（1．4．1）的唯一解，还需验证解（1．4．2）是方程组（1．4．1）的解，也就是要证明

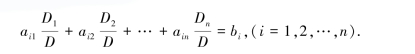
为此，考虑有两行相同的n＋1阶行列式

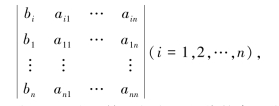
的值为0．把它按第1行展开，由于第1行中aij的代数余子式为

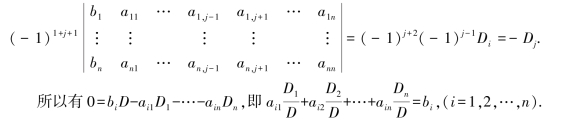
证毕．

例1．4．1　解线性方程组：

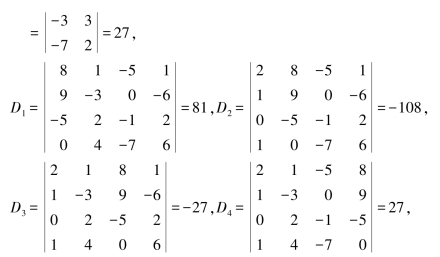
于是得x1＝3，x2＝－4，x3＝－1，x4＝1．

克莱姆法则有重大的理论价值，撇开求解公式（1．4．2），克莱姆法则可叙述为以下两个重要定理．

定理1．4．1　如果线性方程组（1．4．1）的系数行列式D≠0，则该方程组一定有解，且解是唯一的．

其逆否定理为：

定理1．4．1′　如果线性方程组（1．4．1）无解或有两个不同的解，则它的系数行列式必为零．

线性方程组（1．4．1）右端的自由项b1，b2，…，bn不全为零时，该线性方程组叫做非齐次方程组；当b1，b2，…，bn全为零时，该线性方程组叫做齐次方程组．

对于齐次线性方程组

x1＝x2＝…＝xn＝0一定是它的解，这个解叫做齐次方程组（1．4．4）的零解．如果一组不全为零的数是齐次方程组（1．4．4）的解，则它叫做该齐次方程组的非零解．齐次方程组（1．4．4）一定有零解，但不一定有非零解．把定理1．4．1和定理1．4．1′应用于齐次方程组（1．4．4），可得

定理1．4．2　如果齐次方程组（1．4．4）的系数行列式D≠0，则该齐次方程组没有非零解．

定理1．4．2′　如果齐次方程组（1．4．4）有非零解，则它的系数行列式必为零．

定理1．4．2（或定理1．4．2′）说明系数行列式D＝0是齐次方程组非零解的必要条件．在第3章中还将证明这个条件也是充分的．

例1．4．2　问λ取何值时，齐次方程组

有非零解？

解　由定理1．4．2′可知，若齐次方程组（1．4．5）有非零解，则其系数行列式D＝0．而

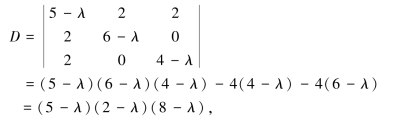
由D＝0，得λ＝2，λ＝5或λ＝8．

不难验证，当λ＝2、5或8时，齐次方程组（1．4．5）确有非零解．