定义6.1.1 被研究对象的全体称为总体或母体,记为X.例如,研究一批电视机寿命,将这批电视机视为总体;研究某市男性大学生身高时,该市男大学生全体为总体;称总体中的每个元素称为个体.例如,每个电视机寿命,每个男性大学生身高都是个体.总体中个体的数量称为总体容量.
注6.1.1 对每个个体来说,它有许多方面的特性,而在实际问题中,人们往往关心的只是个体的某项数量指标.所以说这里的总体实质上是指某项数量指标的全体.例如,研究一批电视机寿命时,其寿命数量指标为总体,取值范围为[0,∞);研究某市男大学生身高时,男性大学生身高取值[1.50,2.02]为总体.
由于每个数量指标的取值是随机的,故总体是随机变量,这样就把对总体的研究转化为对某个随机变量的研究.由于一个随机变量的分布函数全面的描述了该随机变量的统计规律,因此对总体进行研究的一个重要任务就是确定相应的随机变量的分布.今后我们将不再严格区分总体和相应的随机变量,而直接用总体相对应的随机变量X或者相应的分布函数F(x)来表征总体,例如:我们直接称“总体X”或“总体F(x)”.
如何获得总体X的分布函数F(x)的具体形式呢?
我们先来看一个例子:为了确定电子元件的寿命X的分布,当然最精确的方法是对每一个元件的寿命逐一测量,但是寿命试验是一种破坏性试验,并且试验需要花费大量的人力、物力等,并不可取,因而,一般来讲只抽取一部分电子元件来做试验,并通过这些电子元件的寿命数据推断总体的寿命分布.
如上所述,数理统计具有“部分推断总体”的特征.
上面的例子涉及到两方面的问题:
(1)如何获取部分信息,这涉及到统计抽样的问题;
(2)如何利用获取到的部分信息,这涉及到统计推断的问题.
在这一节中,我们首先回答第1个问题.
为了对总体的分布进行各种研究,就必需对总体进行抽样观察.
所谓抽样就是指从总体中按照一定的规则抽出一部分个体的行动.
一般地,我们都是从总体中抽取一部分个体进行观察,然后根据观察所得数据来推断总体的性质.按照一定规则从总体X中抽取的一组个体(X1,X2,…,Xn)称为总体的一个样本,显然,样本为一随机向量.
定义6.1.2 (简单随机抽样)为了能更多更好地得到总体的信息,需要进行多次重复、独立的抽样观察(一般进行n次),若对抽样要求:①随机性:每个个体被抽到的机会一样,保证了X1,X2,…,Xn的分布相同,与总体一样.②独立性:X1,X2,…,Xn相互独立.那么,符合“随机性”和“独立性”要求的抽样称为简单随机抽样,由此得到的样本(X1, X2,…,Xn)称为从总体X中得到的容量为n的简单随机样本,也简称为简单随机样本.
例如,从总体中进行有放回抽样,显然是简单随机抽样,得到的样本就是简单随机样本.从有限总体中进行不放回抽样,虽然不是简单随机抽样,但是若总体容量N很大,而样本容量n很小(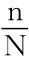 ≤10%)时,则可以近似地看作是放回抽样,因而也就可以近似地看作是简单随机抽样,得到的样本可以近似地看作是简单随机样本.
≤10%)时,则可以近似地看作是放回抽样,因而也就可以近似地看作是简单随机抽样,得到的样本可以近似地看作是简单随机样本.
对抽取的n个个体X1,X2,…,Xn进行试验,相应于每一次观测都得到一组数据x1, x2,…,xn,称xi为Xi的观测值,并称由(x1,x2,…,xn)称为样本观测值.由于样本是随机变量,那么每次观测样本观测值(x1,x2,…,xn)也会不同.于是我们把样本(X1,X2,…,Xn)的所有可能取值构成的集合称为样本空间,显然一个样本值(x1,x2,…,xn)是样本空间的一个点.
定义6.1.2抽样方式有很多,但是今后本书中凡是提到抽样与样本,都是指简单随机抽样与简单随机样本.
定义6.1.4 (统计量)设(X1,X2,…,Xn)是来自总体X的一个样本,g(X1,X2,…, Xn)是样本的函数,若g中不含任何未知参数,则称g(X1,X2,…,Xn)是一个统计量.
设(x1,x2,…,xn)是对应于样本(X1,X2,…,Xn)的样本观测值,则称g(x1,x2,…, xn)是g(X1,X2,…,Xn)的观测值.
例如:(X1,X2)是来自总体X~N(1,σ2)的一个样本,则X1+X2-1,min(X1,X2)都是统计量,而σX1就不是统计量.
数理统计中最常用的统计量:
(1)样本均值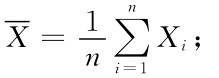
(2)样本方差 i=1
i=1
(3)样本标准方差
(4)样本k阶原点矩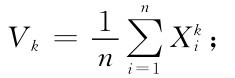
(5)样本k阶中心矩
设(x1,x2,…,xn)为样本(X1,X2,…,Xn)的观测值,则这些统计量相对应观测值分别为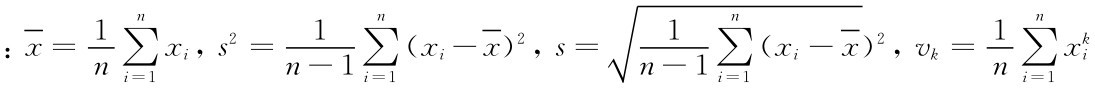 和
和 在不至于混淆的情况下,这些值也分别称为样本均值、样本方差、样本标准差、样本k阶原点矩、样本k阶中心矩.
在不至于混淆的情况下,这些值也分别称为样本均值、样本方差、样本标准差、样本k阶原点矩、样本k阶中心矩.
例6.1.1 设X1,X2,…,Xn为来自总体为X容量为n的样本,且EX=μ,DX=σ2样本均值记 样本方差
样本方差 .试证明:
.试证明:
证 (1)由样本均值的线性性质有:
由于X1,X2,…,Xn是独立同分布的,故有

(2)注意到 我们有
我们有
(3)由(2)及EX2=DX+(EX)2有
注6.1.2 本例的证明并不复杂,但是其结果在数理统计中是很有用的,读者应该熟记.
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。















