拉普拉斯反变换和部分分式法

应用拉普拉斯变换求解线性动态电路暂态过程时，不仅需要根据已知的原函数求象函数，还要根据求得的响应的象函数求其原函数，即要进行拉普拉斯反变换。

求拉普拉斯反变换最简单的方法是查拉普拉斯变换表（见表7-1）。在求解线性动态电路暂态过程中，电压或电流的象函数F（s）往往都是s的有理分式，如果将其展开成部分分式，便可用查表法求出其相应的原函数f（t）。

设象函数F（s）为

式中：N（s）和D（s）都是s的多项式，所有系数a和b都是实常数，m和n是正整数，一般m＜n，即F（s）是真有理分式。设分子多项式N（s）与分母多项式D（s）均不含公因式。为将F（s）展开成部分分式，必须首先求出D（s）=0的根，下面就这些根的不同情况分别讨论F（s）的展开。

1. D（s）=0仅有实数单根

设D（s）=0有n个实数单根，分别为P1，P2，… ，Pn。

则

F（s）可展开为

式中：k1，k2，…，kn是待定系数。为求出每个待定系数，将式（7-16）两边各乘以（s-pj），得

再令上式中s= Pj，则等式右边只剩下kj，其余各项均为零，故得

式（7-17）是确定式（7-16）中各待定系数的公式。

因为F（s） =N（s）/D（s），pj是D（s） =0的一个根，故（s-Pj）是D（s）中的一个因式，按式（7-17）计算kj时，可先将因式（s-Pj）与D（s）中的相同因式消去，然后以s=Pj代入。也可先不消去这个因式，当令s=pj时，式（7-17）变成型不定式，则可用罗必达法则求出kj ：

即

kj确定之后，查拉普拉斯变换表可得

或

式（7-20）有时称为分解定理。

例7-6　已知象函数，求其原函数f（t）。

解　D（s）=s3 +17s2 +66s+72=（s+2）（s+3）（s+12）=0的根为P1=-2，p2=-3 ，P3 =-12。又因D′（s）=3s2 +34s +66，由式（7-18）

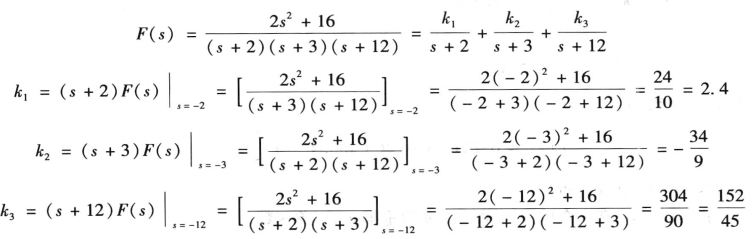
所以

2. D（s）=0含共轭复根

设D（s）=0含有复数根，复数根也属于单根，可用式（7-17）或式（7-18）确定待定系数kj。由于D（s）是s的实系数多项式，若D（s） =0有复数根，则必定是共轭成对的。

设D（s）=0有一对共轭复数根，它们是P1=-α+jω，P2=-α-jω，则F（s）的展开式中一定含有以下两项

其中k1可由式（7-17）求得

式中：| k1|是复数k1的模，θ1是k1的辐角。

由于F（s）的分子多项式N（s）也是s的实系数多项式，则k2必为k1的共轭复数，即

则式（7-21）相应的原函数为

式（7-22）表明，每对共轭复根的分式项对应的原函数是一个衰减的正弦函数。

例7-7　已知象函数F（s）=1/［s（s2 +2s +5）］，求其原函数f（t）。

解　D（s）=s（s2 +2s +5）=0的根为P1=-1 + j2 ，P2=-1-j2， P3 = 0。则由式（7-18）

所以，原函数为

3. D（s）=0含有重根

设D（s）=0有一个单根P1和一个q阶重根P2，则象函数

是一有理真分式，可展开的部分分式为

k1可按式（7-17）求出，即

为了求出与q阶重根相关的各分式的待定系数，将式（7-23）两边各乘（s-P2）q，则有

令上式中s=P2，可得

再对式（7-24）两边逐次求导，并令s= P2，则得

确定了部分分式中的待定系数后，则可以查表得出已知象函数的原函数，即

例7-8　已知象函数，求其原函数f（t）。

解　D（s）=s3（s +1）2 =0有三重根P1 =0和二重根P2=-1。则象函数展开部分分式为

由式（7-25）和式（7-26），得

相应的原函数为