计量分析模型

5.1.1.1　经典的动态因子模型

经济的周期波动是通过一系列经济变量的活动来传递和扩散的，任何一个经济变量本身的波动都不足以代表宏观经济的整体波动。为了反映宏观经济整体波动过程，从许多时间序列经济数据组成的面板数据中，估计出驱动各变量波动的共同因子，是判别和分析经济周期波动的有效工具之一。Geweke（1977）采用动态因子模型提取合成指数研究经济周期。动态因子模型（DFM）是从大量时间序列中提取最重要的不可观测的因子，模型假定几个不可观测（潜在）动态因子ft，它决定了时间序列变量Xt对应的高维矩阵的联动性，同时还有零均值的异质性扰动et，它反映测量误差和具体序列的个体性质。具体形式如下：

其中，Xt=（XI，tX，2t，，…，XNt）是N维时间序列向量，t=1，2…，T。这里假定变量是平稳的、零均值和单位方差；ft=（f1，t，f2t，…，fq，t）是q维的不可观测的动态因子向量，通常q远小于N。L为滞后算子，滞后多项式矩阵λ（L）=（λ1（L），λ（2L），…，λN（L）和Ψ（L）=（Ψ1（L），Ψ2（L），…，Ψq（L），分别是N×q和q×q维的，其中第i个滞后多项式λi（L）称为第i个序列Xit，的动态因子载荷，λi（L）ft称为第1个序列Xi，t的共同成分。经典的动态因子模型假定如下：

假定1：异质性扰动et与因子的新息ηt不相关，即

E（etηt-k）=0，k=1，2，…，K

假定2：异质性扰动之间不相关（包括序列不相关和截面不相关），即

E（eitejs）=0，i≠ j；t，s=1，2，…，T

若（5-1）式为时，称为静态因子模型。ei，t指的是异质性扰动，Λi是共同因子Ft对第i变量的因子载荷向量。静态因子模型指的是Xi，t和Ft的静态关系，但是Ft自身可以是动态过程。

5.1.1.2　单层因子模型

我们首先介绍Khan等（2013）研究中为构建核心通货膨胀指标所采用的单层因子模型。假定消费价格指数πt可以被分解为相互正交的两部分：核心通货膨胀和非核心通货膨胀即其中，被看作所有商品价格波动的共同成分，用来表示价格普遍上涨的通货膨胀压力，而代表CPI的8大类价格以及细类价格变化的特质成分，从而表示非普遍性的价格波动。

在单层因子模型框架下，假定组成CPI的各分类价格πit的变化由两种冲击驱动：一是影响所有各分类价格变化的共同因子Ct，二是仅影响部分分类价格的特质成分eit，即：

πit=ΛiCt+eit（5-3）

其中，Λi为πit对共同因子Ct的载荷。模型允许误差项eit存在截面相关，从而仅影响部分分类价格的因素都被归于特质误差项中。令则单层因子模型可表示为如下向量形式：

我们借鉴Khan等（2013）采用的主成分法对单层因子模型进行估计，即载荷系数的估计为∏t样本协方差矩阵的最大特征值所对应的特征向量，共同因子Ct的主成分估计量为在这种情况下，核心通货膨胀被定义为：即利用CPI对共同因子的估计进行回归所得的拟合值。

5.1.1.3　多层因子模型

Wang（2010）提出的多层因子模型可以将价格波动的来源分解为相互正交的三部分：影响所有价格的全局因子Gt、仅影响第b大类中价格的局部因子以及仅影响单个价格的特质成分因此，对于由CPI各细类价格组成的面板数据第b类别的双层因子模型可以表示为：

其中，b=1，2，…，8，分别代表构成CPI的8大类别，如1表示食品类、2表示烟酒类，i=1，2，…，nb表示第b类别中的第i个价格，例如当b=1，i=1时，表示食品类中的粮食价格。允许存在弱截面相关。我们假定两个层次的因子均为一维，主要是由于目前尚没有估计多层因子模型中因子个数的有效方法，而且这样做会使得因子的经济意义更加明确和易于解释，如表示仅影响食品类价格的冲击，即可能是气候条件、自然灾害等因素有关。另外，这与Khan等（2013）的分析也是一致的。

另外，包含所有8大类别的因子模型可以写为如下形式：

即

Wang（2010）的研究表明，通过以下假定条件，可以将因子空间标准化：对于所有b，为对角阵；在上述假定条件满足时，多层因子模型的所有参数均是可识别的。

根据上述模型分析，我们将单层因子模型中的非核心通货膨胀πnc进一步分为两部分：即消费价格指数πt被分解为相互正交的三部分：核心通货膨胀各大类价格变化，以及特质成分可以表示为：

后文我们将通过方差分解来证明，单层因子模型的价格分解方式将的一部分误归于造成高估核心通货膨胀，将另一部分误归于造成高估单个商品的异质性价格变化。

关于双层因子模型的估计方法，我们采用Breitung和Eickmeier（2014）提出的序贯最小二乘法进行估计。具体估计步骤如下。首先，假定有全局因子和局部因子的初始值分别为：那么，相应的载荷系数可以由如下个回归式得到：

将所得到的估计量记作令将整个模型系统的载荷矩阵记为：

然后，用∏t对全局因子和局部因子进行重新估计，得到新估计量为：

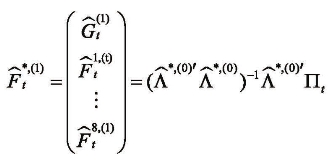
将上述因子的新估计量带入式（5-9）中继续估计载荷系数得到载荷矩阵重复以上步骤，直到残差平方和收敛达到最小值。其中残差平方和为：

由于上述每一步所得的估计量都包含在序贯最小二乘估计量的参数空间中，因此，下一步估计不可能产生更大的残差平方和。最后，序贯最小二乘法会使残差平方和收敛到一个最小值，即：

Breitung和Eickmeier（2014）采用典型相关估计量作为初始值，而我们采用CPI及其8大类别价格指数作为全局因子和局部因子的初始值，这是因为：首先，序贯最小二乘法是一种全局寻优方法，其所收敛到的最小值与初始值的选取无关，采用CPI及其8大类别价格指数作为初始值并不会影响最后的估计结果。其次，由于CPI包含了所有细分价格信息，8大类别价格指数包含了本大类细分价格信息，将其作为全局因子和局部因子的初始值是合理的。第三，避免了典型相关估计量的计算，简化了估计过程。将收敛结束后的全局因子和局部因子的估计量分别记为为了施加前面的标准化假定条件，需要每一个（b=1，…，8）对进行回归，将回归残差作为与正交的新的局部因子估计量（b=1，…，8），并将（b=1，…，8）进行标准化（即均值为0，标准差为1）得到最终估计量和最后，利用CPI对进行回归，将其拟合值作为核心通货膨胀指标的度量。