稳健性质量设计基本原理

第一节　稳健性质量设计基本原理

田口博士的稳健性质量设计（robust product design，RPD），又称健壮设计、三次设计。是充分利用系统的非线性性质，通过合适地选择可控因素的位级组合，使产品性能对各种干扰（内干扰，外干扰，物品间干扰）最不敏感，从而达到提高产品质量和降低成本的目的。这是一种最新颖、科学、有效的质量优化设计方法。

一、稳健性设计中的产品质量特性

对什么是质量，田口博士对质量的概念赋予了新的内涵，他认为：“所谓产品质量，就是产品出厂后给社会带来的损失，但其中除去机能本身对社会造成的损失。”他不同意把质量问题作为价值观念来研究。例如，水具有关系人的生命问题的巨大价值，但它的价钱却比同人的生命无关的金刚石低得多。如何评价产品的价值是属于市场销售的问题，而产品质量是由它出厂后给社会带来的损失来评定的，这个社会损失包括两个方面：由于机能波动造成的损失和由于弊害项目造成的损失。

田口博士还认为，为了减少产品出厂后给社会带来上述两类损失的对策，就是产品质量管理。对此，下面要说明几个问题：

1．为什么要把机能本身给社会造成的损失除外呢？田口认为，对产品机能本身而言，它可能对社会造成损失，但减少这种损失，并不属于质量的问题。例如，酒的功能具有醉人的效果，因酗酒对社会造成的损失不少，但如果生产一种不醉人的酒，可能就不成为酒了。如此等等。

2．什么是机能波动损失？质量特性的波动是一种客观存在的现象，产品在设计时，其质量特性必有一个规定的理想目标值，但是在制造过程中，由于种种因素的存在，不可能每一种产品的实际质量特性都正好符合目标值，相互间会有一定的差异。公差制度就是这一客观事实的要求。此外，产品在使用过程中存在着外部和内部两类干扰，也会使质量发生波动。

此外，还可能有某些偶然性的原因，也都会造成质量的波动，也就是质量特性偏离原来的目标值。这种偏离，必然会给社会带来损失。例如，当波动的范围超过质量特性所规定的界限时，就可能要送去修理或报废，这就属于机动的波动损失等。

3．什么是弊害项目造成的损失？这里的弊害，通常是指产品的副作用，如有的药品用于治疗某种疾病效果可能很好，但它可能有别的不良副作用。有些产品能很好的实现某种规定的功能，但它可能有噪音，这些弊害也可以对社会造成损失。

稳健性质量设计中的质量特性按期望的数值种类有以下三种：

（1）望目特性。希望特性值存在一个目标值m（m≠0），并希望实际的特性值围绕目标值波动，波动量越小越好。例如，机械零件的制造尺寸及配合公差等。

（2）望小特性。希望这种特性越小越好（但不取负值），波动也越小越好。如零件的磨损量、机器的噪声、振动等。

（3）望大特性。这种特性要求其数值越大越好（亦不取负值），波动也越小越好。如机器的效率、构件的强度和疲劳寿命等。

质量特性又可分为动态特性和静态特性两种。动态特性的数值一般随输入信号和环境条件的变化而变化。静态特性则反之。动态特性数值随输入信号的变化而改变的称为主动型动态特性；而另外一类随环境或用途变化而变化的特性则称为被动型动态特性。例如，汽车的操纵特性，机床的切削特性都是主动型的，而像传感器的测试特性等都是被动型的。

二、质量波动及其影响因素

影响产品质量特性波动的因素很多。按照人们能否可以控制、可否明确其影响的等级和水平可分类如下。

1．可控因素。这是指大小（或水平）可以比较，且可人为地选择或控制的影响因素。例如，零件的表面质量特性值——粗糙度，在同一机床条件下，其数值与刀具几何形状参数、零件加工时选用的切削速度、进给量等有关。这些量就是评定机床加工质量特性的可控因素。

2．标示因素。这是指使用产品时外界环境因素、使用条件等。它们的数值大小（或水平）在技术上虽然可以确定，但不能主观加以选择和控制。例如，动力电源的电压和频率、环境温度和湿度等，一般不是人们所能改变的。

3．信号因素。这是为实现某种需求而选取的对产品输入的改变，它是按专业需求和实际经验而加以确定的，不能任意指定。例如，汽车的转弯半径与方向盘的转角有关，这个转角就是信号因素。一般要求信号因素的水平应容易改变，且与产品的输出特性呈线性关系，以利于产品特性的校正与调整。

4．区组因素和误差因素。区组因素有大小（水平）之分，但并无技术上的意义。它是指试验设计时为减少试验误差而确定的因素。例如，加工零件时不同操作者、不同原材料、不同班次、不同设备等。误差因素是指除上述因素外，对产品质量特性有影响的其他因素的总称。

进行稳健性质量设计时，设计人员应找出对质量特性可能最有影响的若干因素，并在明确标示因素水平并考虑其影响的基础上，采用田口三次设计方法（见第二节），调整可控因素，找到最佳因素组合，使产品的质量特性在误差因素水平影响较大的情况下，达到质量特性最稳定。再运用输入信号因素变更，达到所需的质量特性值。最后，通过控制对特性稳定贡献最大的误差因素，达到设计出质量好、成本低的产品的目的。

三、信噪比

信噪比（Signal Noise Ratio：SN比）作为通信系统的质量指标，已经有近百年的历史。田口博士把SN比的概念引入试验设计技术，用于系统或产品的开发设计。

1．SN比的定义。设产品的质量特性γ在诸因素的作用下为一随机变量，它的数学期望为μ，方差为σ²。一般情况下，希望μ值越接近目标值越好；同时也希望σ²值越小越好，因为σ²值反映的是实际特性值偏离μ值的离散程度。

在概率统计学中，常用变异系数γ＝σ／μ来表示实际值可能偏离μ值的程度。在三次设计中，引入了一个新的评定指标η＇＝μ²／σ²用来评定产品质量特性的稳定性。因为在μ一定的情况下，σ²越小，η＇值越大。所以，η＇值越大，质量特性波动越小。把式中μ²值看做信号，σ²值看做人们不希望有的噪声。因而，称η＇为信噪比，用做反映产品或系统质量稳健性的重要指标。

在实际计算中，模仿通信理论中的处理方法，将η＇值转化为分贝值（dB值）。用下式计算：

η＝10lgη＇

这样做的目的是使η值较接近正态分布，且使效应也基本具有线性可加性，便于今后用方差分析的方法进行统计处理和分析。

2．各类质量特性值的SN比计算式。

（1）望目特性值的SN比计算式。若对n件产品，测得望目特性Y的数据为：

y₁，y₂，…，y_n

则μ、σ的无偏估计分别为：

引入下面的记号

则μ2的无偏估计量为：

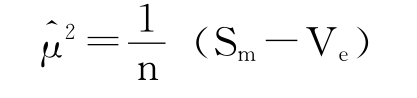
SN比的估计量为：

以分贝（dB）表示的SN比为：

（2）望小、望大特性值的SN比的计算值。设产品的质量特性值Y－N（μ，σ²），对于望小特性值是希望Y越小越好，因此也等价于μ越小越好；同时也希望波动越小越好，即希望σ²越小越好。为此，可令望小特性值的SN比值为：

η＇＝1／（μ2＋σ²）

此时，η＇越大，对应于μ2、σ²越小，即产品质量特性值和波动均为最小。

由统计理论可知，

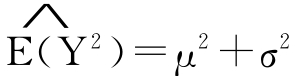
若Y的n个观测值为y₁，y₂，…，y_n，可知E（Y²）的无偏估计为：

于是，η＇的无偏估计为：

SN比的分贝值为：

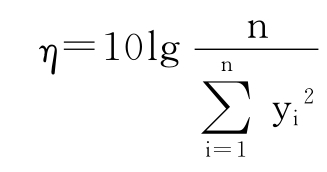
此即为望小特性SN比的计算式。

对于望大特性SN比的计算式，只要将特性值Y取倒数，即可按望小特性值处理。不难求出，望大特性值的SN比的分贝值计算式为：

（3）动态特性值的SN比计算式。设产品的动态特性值为Y，其均值μ随着信号M的变化而变化；同时，信号因素M与μ为线性关系，且

μ＝α＋βM

由于存在误差因素的干扰，动态特性的实际值：

μ＝α＋βM＋ε

式中：ε为误差因素引起的误差，一般服从正态分布ε－N（0，σ²）。

对于动态特性，希望信号因素的线性效应的影响越大越好，即｜β｜要大；而各种内外干扰的影响越小越好。因此，可定义动态特性的SN比为：

式中：β为输出特性值Y的线性系数；σ²为误差的方差，表示误差因素变化产生的影响大小。

利用一元线性回归理论及方差分析可求得β的估计值和误差方差估计值σ²。最后，通过变换后可得到用分贝表示的信噪比计算式：

（4）灵敏度的估计公式。信噪比公式中的μ是反映平均特性的指标，称为灵敏度。它的

无偏估计为：

同样，灵敏度SN比分贝值的计算式为：

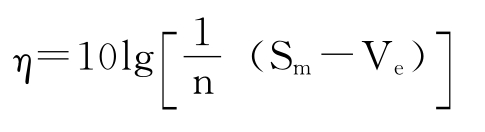
四、稳健性质量设计的主要内容

稳健性质量设计主要包括两方面的内容：

（一）“脱线（off－line）”质量设计与管理

“脱线（off－line）”QE，属于生产线以外的质量，所以又称“线外质量”。主要研究产品的研发设计和生产工艺设计阶段使产品质量优质、低成本、功能稳定可靠的质量控制方法。田口提出了“质量损失函数”的概念，并把产品设计分为系统设计（系统选择）、参数设计和容差设计三个阶段，进行质量参数优化设计。

1．质量损失函数。质量损失函数的公式为：

L（y）＝K（y－m）²

式中，m为某一质量特性的目标值；y为该质量特性的实际值；K为一常数；L（y）为质量特性；实际值为y；偏离目标值为（y－m）时的社会损失。

什么是社会损失呢？就拿农民所使用的塑料薄膜来说，制造商为了节约原料，降低产品成本，希望尽量减薄塑料薄膜的厚度，以致使薄膜的厚度总是接近于规格的下限，这样就可能给社会造成以下损失：薄膜容易破裂，农民须重新购买；庄稼遭受损失，农作物减产，农民减少收入；由于农作物损失，造成物价上涨，使社会受到损失，而社会损失，又必须承担追加成本。

在这种情况下，生产厂商为了节约少量的成本，可能使社会损失增大若干倍。田口认为，这样的制造商“比贼更坏”。小偷偷了100元，社会损失就是100元，但制造商为了节约10元钱将可能造成上千上万元的社会损失。

损失函数可以帮助企业确定改进质量的优先项目，因为从损失函数看，质量就意味着用低成本满足使用要求，同时也意味着目标值的均衡性。损失函数能够正确评价为改善质量而进行的投资是恰当的，这就克服了企业内部成本抵制系统对提高质量的障碍。在田口损失函数的基础上，可以确立使社会损失达到最小的容差（公差）设计方法。

2．质量特性参数的优化设计。田口从某些质量的输出特性与影响输出特性的参数组合之间存在着非线性的关系出发，提出了一套选择最优参数组合的方法。他认为过去设计人员在选定参数时，只要能满足输出特性的目标值就满足了，而不考虑如何保持输出特性的稳定性，这是一种笨拙的设计。实际上，由于存在着参数组合同输出特性之间的非线性关系，就有可能找到一种最佳组合方式，使输出特性存在内外干扰的情况下尽可能保持稳定，从而保证质量的可靠性。为了使输出特性保持稳定不变的最佳参数组合，未必能保证达到输出特性的目标值。为此，常常需要在结构系统中加入一个线性元件，以达到目标值的要求。

总起来说，田口博士把新产品的开发（或新生产方式的开发）分为产品规划、系统设计、参数设计、容差设计四个阶段。

产品规划阶段是估计或预测具有何种机能的产品容易销售，需求量的情况如何等，这是决定是否或如何开发产品的阶段。系统设计阶段是按产品规划所决定的机能来开发产品的阶段，也是总体设计的阶段，这个阶段做得如何对整个产品质量具有重要的意义。参数设计阶段是对系统中各个部件、各个参数确定最佳水平组合的阶段，其目的是使质量和成本都得到改善，也是实验计划法应用的最重要领域。容差设计阶段系统参数的中心值（目标值）确定以后，确定允许的波动范围，就是要综合考虑到质量与成本的平衡问题，也是实验计划法有效应用的场合。

（二）“在线（on－line）”质量设计与控制

“在线（on－line）”QE，又称线内质量，属产品的生产制造阶段。主要研究生产过程中有关质量控制的技术。它包括工序的诊断与调节、预测与校正调节方式的设计以及产品的检验与处理等方面的内容。

1．工序诊断与调节。工序在生产过程中，由于各种因素的影响，不可避免地会产生某些故障，这些故障自然会影响产品的质量。就像人们在生活中一样，经常可能发生一些伤风感冒之类的小病，这时应该请医生看一看，做些诊断，然后吃些药，很快就会恢复健康。生产过程中工序出了故障，也应该请专家进行诊断，查一查究竟出了什么毛病，是机器设备问题？还是加工操作或材料问题？然后对症下药，采取措施进行纠正，以恢复生产过程的正常状态。田口博士把这个工序质量管理的过程称之为工序的诊断与调节。更具体地说，工序诊断就是要通过检测等手段，考查或判断工序是否正常，是否出现了不良品；而工序的调节就是当发现生产过程中工序出现不正常或出现了不良品时，采取必要的措施消除产生不正常的原因，恢复工序的正常生产状态。

田口在解决这个问题时，也是从经济的角度来考虑的。从一方面看，为了防止出现不良品，最好每生产一个产品，都进行检查，以便及时发现是否出现不正常情况，这样做，当然可以大大减少不良品损失；但另一方面又可能大大增加检查费用，所以田口建立了一个诊断调查的费用函数，以便得出一个最经济的诊断间隔期。

2．预测与校正。这是工序质量管理中一种反馈控制方法。它的主要特点是：一旦发现工序生产不正常，就通过调整参数（或称信号因素）水平进行校正，以恢复其正常状态。所以，预测与校正的实现，必须具有可以对偏差进行校正的信号因素。这里的偏差是指在生产过程中某一质量特性的实际测量或预测值与要求达到的目标值之间的差异。例如，机械制造中热处理时实际或预测温度与规定温度的差距，轧制钢板时的实际厚度与要求厚度之间的差距等。信号因素是指可以用来校正实际或预测值同目标值的偏差的可调因素。例如，司机的方向盘就可以用来调整或改变行驶方向；增加燃料就可以改变温度；改变轧机的压力就可以使轧制钢板的厚度更接近目标值等，这就是信号因素。

所以说，预测和校正是对于某一所要控制的计量特性值，每隔一定时间进行一次检测，根据所测得的数值，预测生产继续进行时到下一次测量时间点这段时间内所生产产品的质量特性值的平均值。例如，预测值与目标值偏离，为减少偏差，则需改变用于修正的信号因素，以期达到更接近目标值的要求。

3．检验与处理。工序的诊断与调节，预测和校正，都是在生产过程中进行的，而检验与处理则是对工序完工后的制成品来说的。田口博士认为，产品或零件加工完成后，可以进行全检，把不合格品剔出以后再出厂，这样就可以防止因不合格品漏检而送到用户手中所造成的损失。确定检验或不检验的准则，就是要确定临界的不合格品率p₀，当企业生产该种产品的实际平均不合格品率p大于临界不合格品率时，应该进行全检以后再出厂；而当实际平均不合格品率p小于临界不合格品率p₀时，则可以考虑不检验就出厂。检验与处理就是围绕着这一中心思想进行检验方案的设计，并确定在各种不同情况下计算临界不合格品率的方法。