数学概念的表征

二、数学概念的表征

数学概念是所有陈述性知识的基础，也是思维的基本单位。从数学概念的获得过程分析，数学概念具有过程特征和对象特征的二重性，活动过程的概念表征与获得结果的概念表征有不同的心理机制；从概念之间各关系角度分析，概念之间具有横向的映射与对应的联系结构与纵向的层次结构所形成的概念联系网络结构。

1．数学概念的结构及其表征

数学概念包括类别（对象集合S）、特征（对S中元素的共同特征的描述）和模型（S中的元素）三个要素，如初中“函数”概念中，类别指的是两个变量之间的各种依存关系：像匀速运动物体中的运动时间与位移之间的关系、某地气温与时间之间的关系、在销售价格确定的情况下销售收入与商品销售量之间的关系等；特征指的是两个变量之间的本质联系：当自变量确定时，函数值唯一确定；而模型指的是个体把类别中的某一个对象作为“函数”的代表经过加工保存在自己的记忆中——形成概念的意象表征。

1．1数学概念的过程特征的表征。它指的是学生形成概念的思维操作过程中对概念的表征。这种表征是伴随着学生形成数学概念的过程而体现出从模糊到清晰的过程，数学概念的形成过程从概念类别分析有两种形式：①概念同化是通过特征添加来研究概念类别集合的子集；②概念顺应是对一类概念类别的特征进行再抽象后所形成的新的类别集合；这两种形成方式都是在概念联系中表征新的概念。在形成初中“函数”概念的过程中，学生大脑中首先具有各种不同的变量之间对应关系的辨别、分类过程，从中形成对函数概念的过程特征的理解，而且初中“函数”定义是结合过程特征进行的：“在某一变化过程中有两个变量，如果对于一个变量x在某一范围内的每一个确定的值，另一个变量y都有唯一确定的值与它对应，那么y就叫做x的函数，x叫自变量”，而在体验这种过程特征时，图形、图式与意象具有重要的作用。

学生在形成数学概念的过程阶段对概念表征的心理模式是“模型＋特征＋概念联系”。

模型是对象集合中的元素，是个体聚焦而且在大脑中留下鲜明知觉的一种意象，特征是个体对模型意象的一种意义注释（用语言文字或数学符号），例如，尽管数学上有圆的各种等价的定义，但学生头脑中对圆的意象表征“Ο”是占据中心位置的表征方式，学生对圆的线段运动定义、点集定义、轨迹定义、坐标定义（方程）的理解和记忆都需要建立在对圆的意象进行特征分析的基础上，意象是个体大脑中建立的数学概念的内在知觉对应物，数学概念的意象表征往往具有直观的视觉表象，具有形象性。

1．2对数学概念的“对象”特征的表征，是在对“过程”特征表征的基础上进行缩略——以语言符号或图标的形式进行表征，这种缩略的神经机制是神经激活扩散的模块化。由于学生的个体差异，他们的概念“过程”特征与“对象”特征的表征阶段的边界并不清晰，有时是以共存的形式出现的，这就导致了数学概念表征的差异性：不同的个体对同一数学概念可能用不同的表征方式。

如关于“函数”的概念，有的用形式记号f（x）表征，有的是用函数图像，甚至更为具体的函数图像（一元二次函数图像）进行表征。

意象表征具有片面性，意象的片面性指的是个体的概念意象不一定能反映概念的本质属性，例如，学生关于“函数”的概念意象就有以下错误：函数只对应一个法则，所以分段函数不是函数；函数图像应该是连续的，所以取整函数不是函数；函数自变量的变化必定会引起因变量的变化，所以f（x）＝8，x∈（1，2）不是函数；函数一定包含代数表达式，所以y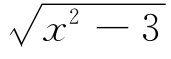＝±是一个函数。而下列对应关系则不是函数：在若干次数学测试中，小明的成绩分别为67分、84分、95分、80分，因为根本就找不到一个代数表达式与之对应。

意象表征的缺点主要靠特征表征和概念联系表征来弥补，如对与圆，我们可以用下面的综合表征模式：

概念表征的意象性来源于个体接受到的大量的具有相同特征的视觉刺激所引起的空间表征加工，这种空间加工在大脑中能进行定位，如颜色与形状等客体特征是从枕页到颞页的腹侧视觉通路上的层级连接区域得到表征的，而运动等空间特征是在从枕页到顶页的背侧通路上得到表征的。由于这些加工具有同时激活的自动加工特征，因此具有使用注意资源的最小性，导致使用图形和空间表征的喜好，即使在代数概念和抽象概念的表征中，也往往借助于意象图形（图式）来表征，如在学习函数时，用图形作为意象进行表征，在学习有理数的加减运算时，用数轴上点的运动来理解运算的意义，即使在学习群、环、域等抽象概念时，学生还是需要寻找到先前学习过的数、式、变换等意象来帮助理解这些抽象概念。另一方面，数学概念的表征需要在意象的基础上添加数学特征注释，如果没有数学特征的捆绑，就只能形成概念的表象而不能形成数学概念的本质，如果不对“圆”的意象进行特征注释，对“圆”的理解就只能停留在模型识别水平（那不是数学）而不能形成对“圆”的概念的本质表征，也就是说，不能建立起表达视觉意象“○”与表达“圆”的数学特征之间神经局部网络的同步激活机制。如下图：

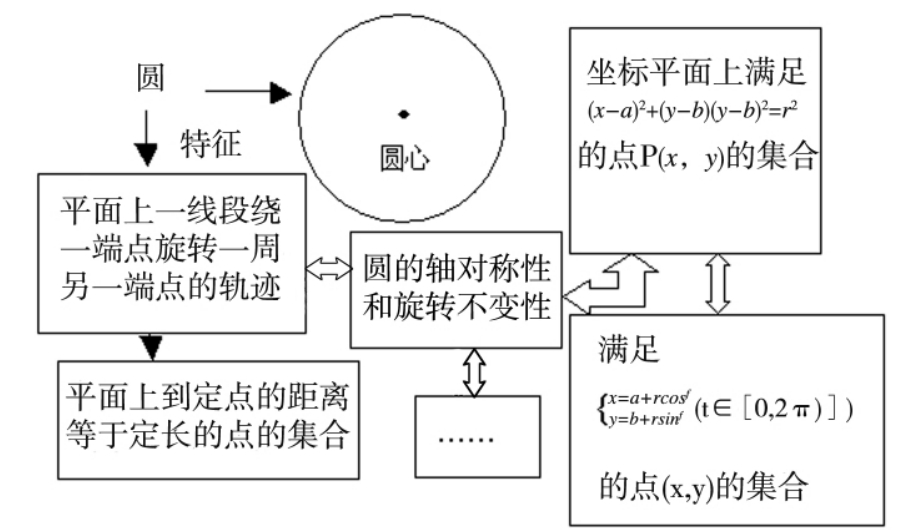
图4－2－1

2．概念之间联系的结构与表征

数学概念之间具有联系的广泛性和良好的系统性，概念之间联系的方式有横向的同级联系（等价、对偶、对应）和纵向的层级联系（抽象），因此数学概念的表征往往需要用低层级的概念来表征高层级的概念。数学中的相互关系有很多种，但基本的关系是序关系、运算关系和映射关系。

图4－2－2

2．1定义：对于集合A、B，则A×B的任意一个子集R就叫集合A、B之间的一个关系（如图4－2－2），如果对于a∈A，b∈B，叫a、b之间具有关系R，记做aRb。

2．2序关系与概念抽象：

对于集合X，如果R是X×X上的二元关系（也叫X上的二元关系），R满足下面条件，则叫R是X上的序关系：

Aa∈X，aRa；（自反性）

若aRb，bRc，则有aRc；（传递性）

若aRb，bRa，则a＝b（反对称性）

在数学概念体系中，强抽象（从一般到特殊）和弱抽象（从特殊到一般）都符合这种序关系的要求，因此数学概念的强抽象和弱抽象是一种序关系，另外，任何其他符合序关系的抽象叫广义抽象。如果一组概念满足C₁R₁C₃R₃A R_nC_n，表达式中的R_i（I＝1，2，…，n－1）表示弱抽象、强抽象或广义抽象3种数学抽象关系中的一种，则称C₁R₁C₂R₂C₃R₃A R_nC_n为一条概念链；如果2条概念链的交集非空，则称这2条链相交；如果m条概念链中的每一条都至少与其余的一条链相交，则称m条链所组成的概念网络的图式为概念系。

数学概念强抽象和弱抽象的概念类别之间的关系是：

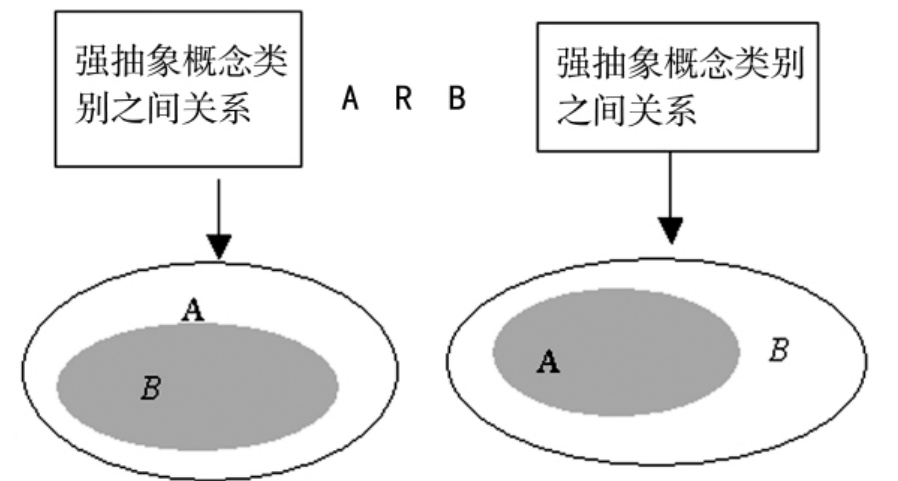
图4－2－3

因此对应着心理上的强抽象和弱抽象的是概念类别之间的包含（被包含）关系。人们可以用概念的抽象关系（概念链、概念系）对数学概念进行分类表征，如对有理数与有理式概念关系可以用如图4－2－4的概念系进行表征：

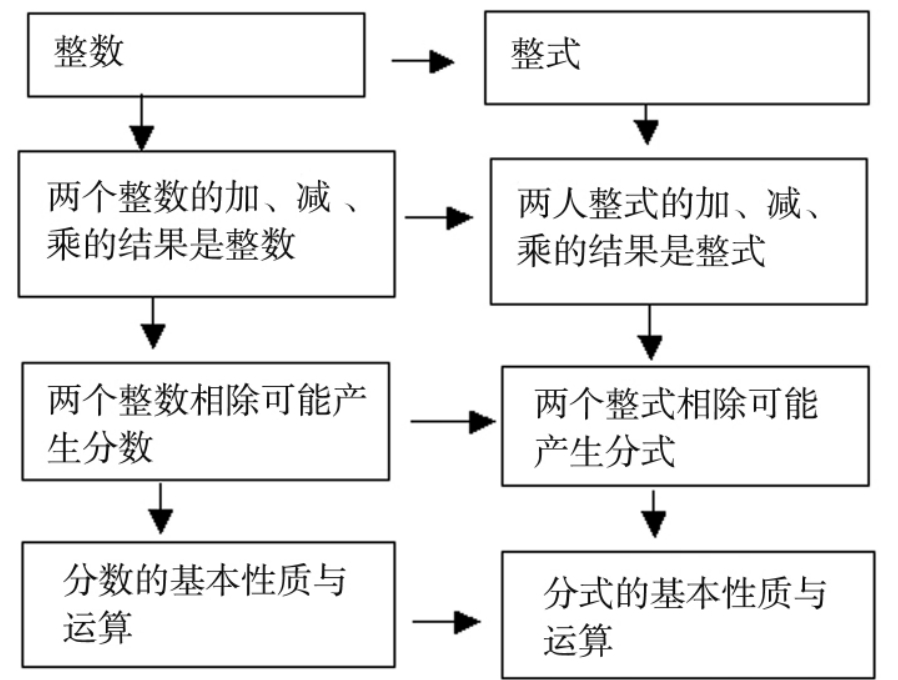
图4－2－4

一方面，从整数到有理数和从整式到有理式是一种通过运算产生的弱抽象，另一方面，从数到式通过把数的一般化而进行弱抽象，但抽象过程的相似性为在学生的心理中产生类比的思维活动奠定了同态结构相似表征的基础。

2．3等价关系与概念域。

如果集合X上的关系～满足下面条件，则叫关系～为等价关系：

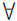a∈X，a～a

若a～b，b～c，则有a～c

若a～b，则b～a。

与数学概念a的表征等价的不同表征模型的集合叫a的概念域。如果两个数学对象具有等价关系，则在大脑中用概念域的方式来表征它们之间的相互关系，像具有相似、全等、同解、相等、平行、同构、同态等映射关系的数学概念（对象），用概念域的方式对这些对象进行表征。人们可以用等价关对对象进行分类，其内在的表征方式是以概念域为基准进行的分类表征，而概念域表征方式的认知神经学证据是人脑信息加工具有局部特异性。

2．4概念之间的对偶关系及其表征。

对偶空间的定义：对于线性空间V，V上的一切线性泛函的集合L（V）叫线性空间V的对偶空间。L（V）可以理解为从V到实数（或复数）域的线性映射的集合。

例如：设有实数域或复数域上的线性空间X到Y的线性变换式：

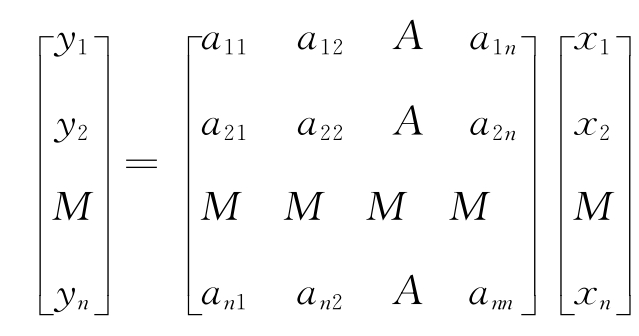中，如果矩阵是一个满秩矩阵，那么线性空间Y与线性空间X就是对偶的空间，系数空间也叫变量空间的对偶空间。如果令n＝2，a₁₁＝a，a₁₂＝bi，a₂₁＝c，a₂₂＝di，当X为实数空间时，Y就是复数空间，因此实空间与复空间具有对偶关系，虚数空间与实数空间是对偶空间。

还有，实系数多项式空间Y＝｛a₀＋a₁x＋a₂x²＋Λ＋a_nxⁿ｝＝［a₀ a₁ Λ a_n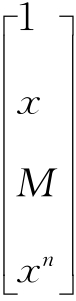］是系数空间｛a₀ a₁ Λ a_n｝的对偶空间，也是变量空间（1　x Λ xⁿ）的对偶空间。

平面上的点与起点在原点的向量是同构的线性空间，如果把平面上点（a，b）所对应的向量旋转一个固定的角度得到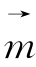向量，则向量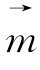的集合与向量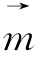的集合就具有对偶关系，特别地，把一个向量空间中的每一个向量旋转90°得到自己的一个对偶的向量空间，例如，圆上的所有点对于旋转变换运算构成一个以圆心为起点的向量空间，那么过圆上的点作切线，这些切线所代表的向量也构成一个向量空间，这两个向量空间是对偶空间，这就是圆上的点的性质与圆的切线性质具有对偶关系的内在原因：

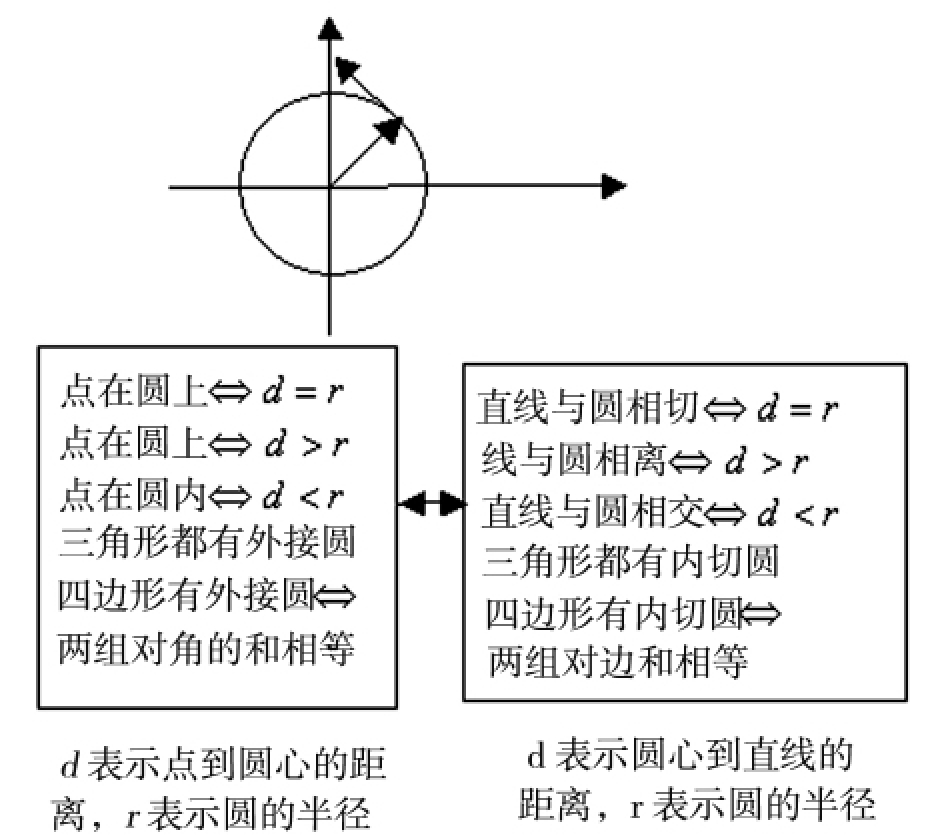
图4－2－5

学生对概念的对偶关系的表征是最薄弱的，因为教师在教学过程中往往忽视这种概念之间的关系，但对偶思想是现代数学的基本思想之一，我们有必要在教学过程中引导学生用合适的方法表征概念之间的对偶关系。学生对对偶关系的表征是用类比的方法通过图式相似改造来进行表征，如用实数的分类图式改造后变成复数的分类图式，实数运算表征改造成复数的运算图式，甚至有的学生直接把实数的序关系表征图式直接用到复数的表征，造成对复数的错误表征。因此，概念对偶关系表征中要注意概念之间的本质联系与区别，把原来的表征图式进行相似改变时应特别注意概念之间的区别，防止出现表征的扭曲。

3．数学概念表征的特点。

3．1数学概念表征的意象性。

在数学概念的表征中，意象具有中心地位。首先，数学概念的表征起源于意象，学生首先要通过对数学概念的类别对象进行分类，明确对象的集合边界，然后选取具有典型性的对象作为概念的代表进行加工，建立概念的模型。其次，学生大脑中保持的往往是一种概念的意象而不是语言符号，学生对数学概念的表征图式是意象为主体的附加意象各种注释的带有过程体验的综合体。

3．2数学概念表征的综合性。

由于意象是对数学概念直观表象，它具有片性，因此需要对概念进行命题和语言符号的注释，进行概念之间联系的概念域和概念系的表征，如图4－1是综合运用意象、语言符号和命题对圆的概念进行表征的例子。

3．3数学概念表征的多样性。

由于学生的学习经验、认知水平和认知加工方式的不同，对同一个概念可能有不同的表征方式，表征没有对错，只有好差，学生可能有不同的概念意象和不同的意象注释，数学教学中可以通过讨论和交流，改善学生的概念表征方式，建立概念之间的广泛联系。

3．4数学概念表征的二重性。

有些数学概念（尤其是代数概念）具有二重性：既表现为一种过程操作，又表现为对象、结构。例如a＋b，既代表2个不相交集合中的元素合并或添加起来的过程，又代表合并或添加后的结果。正是数学概念的二重性，导致了它在表征时的二重性，作为过程操作以程序性知识产生式系统的方式表征，作为对象、结构则是以陈述性知识中的概念表征方式进行表征。形成一个数学概念，往往要经历由过程开始，然后转变为对象的认知过程，而且最终结果是2者在认知结构中共存，在适当的时机分别发挥作用。如学习函数概念，总是先按表达式找若干个自变量的值，去计算对应的因变量的值，再把它变为一个以定义域、值域、对应关系3要素构成的对象。一般来讲，数学概念表征与这个顺序相吻合，但有时会根据具体的问题情境作过程表征，或作对象表征，甚至过程与对象共存的表征。

3．5数学概念表征的发展性。

随着学生学习经验的积累和知识的增长，对数学概念的表征也在不断完善。学生概念表征是沿着过程＋意象→意象→意象＋注释（图式）→语言符号→概念网络的模式进行不断完善的。如“三角函数”的概念，先从直角三角形的边、角关系发现角度与边的比值之间的关系（过程），建立角度变化与比值变化的对应关系，把原来的函数概念（实数上的对应关系）扩展到角与实数之间的对应关系——三角函数（泛函），这时，学生以角度与实数之间的对应关系来表征三角函数，到高中后，利用单位圆定义三角函数，同时通过单位圆上的弧把角度转化为实数值，使三角函数纳入到函数概念体系中，同时建立起三角函数的第一个意象：单位圆中的有向线段，再通过利用单位圆画三角函数图象建立起三角函数的另一个意象——函数图象，这样，对三角函数的表征便有了图象这个形象的意象工具，然后研究三角函数的周期性、单调性、对称性，对三角函数图象进行注释，形成概念图式，在此基础上，把三角函数作为对象进行各种运算（符号化），并建立三角函数与现实生活中联系，与其它概念之间的联系，建立概念网络。