劳斯赫尔维茨稳定判据

劳斯赫尔维茨稳定判据分别由劳斯和赫尔维茨独立提出，该判据可以不求解系统特征方程根，而直接由特征方程系数来判别系统是否满足稳定的充分必要条件。劳斯判据和赫尔维茨判据具有不同形式。劳斯判据采用劳斯阵列，不受系统阶数限制，如果系统不稳定还能得出特征方程有几个根在s平面的右半部。赫尔维茨判据则采用赫尔维茨行列式，但四阶以上赫尔维茨行列式计算较麻烦。劳斯 赫尔维茨稳定判据在计算机技术不发达时是分析处理高阶系统的有力工具，即使现在能通过计算机软件得到高阶系统的根，还是常用稳定性判据来确定参数可行域。目前常采用劳斯阵列形式进行稳定性判定，并称为劳斯赫尔维茨稳定判据，以表示对他们俩工作的认可。

劳斯阵列由系统特征方程系数按一定规则构成，它的第一列元素的符号用于判断系统稳定性。设系统的特征方程为

D（s）＝a0sn＋a1sn－1＋…＋an－1s＋an＝0

对应的劳斯阵列如下：

式中

上述劳斯阵列构成规则简要说明如下：

（1）竖线左边列写出s幂次作标识，由上而下按s最高幂sn至s最低幂s0依次排列。

（2）由特征方程系数列写第一行和第二行各元素，即由s最高幂项系数开始，按幂次的奇偶依次填入第二行，直到s0项系数。最后一个系数若不存在则用零补全。

（3）自第三行开始至s0行各元素由分式运算而得，分母为该元素上一行的第一列元素；分子为四个元素构成的子行列式的负值，这四个元素为上两行中第一列两个元素和该元素所在列的后一列两个元素，具体如b1，b2，c1，c2，d1，d2所示。

按照上述规则可构成任意阶系统的劳斯阵列，并依据劳斯赫尔维茨稳定判据判定系统的稳定性。

劳斯赫尔维茨稳定判据为：动态系统稳定的充分必要条件是劳斯阵列第一列元素不改变符号。如果该列元素改变符号则系统不稳定，符号改变次数等于系统特征方程含有正实部根的个数。

［例4-05］ 试采用劳斯赫尔维茨稳定判据判断［例4-03］系统的稳定性。

［解］ 根据特征方程系数列出劳斯阵列

该系统的劳斯阵列第一列元素符号改变2次，即由3／2变为－1／3，再由－1／3变为10，系统有两个根位于s平面的右半部，系统不稳定。虽然未解出5个特征根的具体值，但与稳定性相关的特征根在s平面的分布信息已完全得到，得到与［例4-03］一致结论。

在计算劳斯阵列时，可以用一个正数去乘或除某一行各元素，如例中第s4行各元素除以3，所得结果将不变。

在构造系统劳斯阵列时，可能会出现下列两种特殊情况：

（1）劳斯阵列的第一列某元素等于零，而其余各元素不全等于零。

这时可用一个微小的正数ε代替这个为零的元素，然后继续进行计算，完成劳斯阵列。

［例4-06］ 设系统的特征方程为s4＋2s3＋3s2＋6s＋1＝0，试判断该系统的稳定性。

［解］ 列系统劳斯阵列如下

用微小正数ε代替s2行第一列为零的元素后，所得到的劳斯阵列的第一列元素改变符号两次，故系统不稳定，且特征方程有两个根在s平面右半部。

（2）劳斯阵列中某一行元素全部为零。

［例4-07］ 某系统的特征方程为s5＋s4＋5s3＋5s2＋6s＋6＝0，试判断该系统的稳定性。

［解］ 列系统劳斯阵列

当劳斯阵列计算到s3行时，出现全行为零的情况，由于此时劳斯阵列第一列元素不全为正，故系统可能不稳定或处于稳定边界。

为进一步了解系统特征方程根的分布，采用如下方法继续完成劳斯阵列。先用该全零行的上一行（s4行）元素作为系数构成一个辅助方程

s4＋5s2＋6＝0

再将上述辅助方程对s求导一次，得

4s3＋10s1＝0

然后用求导后方程的系数代替全零行（s3行）的元素，继续完成劳斯阵列。

由上面劳斯阵列可见，其第一列元素未改变符号，故s平面右半部没有系统特征方程的根。

通过求解辅助方程可得系统特征方程的数值相同而符号相反的两对根为

此外，还很容易求得特征方程另外一个根为s5＝－1。该系统有两对特征方程的根在虚轴上，系统处于稳定边界。

上述这种情况的出现，往往是全零行的上面两行的对应列元素相等或成比例。当存在部分特征根关于原点对称时（见图4-10的几种情况），便会出现这种情况。因为对称是成对出现的，因此全零会出现在s的奇次行中，辅助方程必定为s的偶次幂方程，其根成对出现。辅助方程的阶次也表明了对称分布的极点个数。

图4-10 s平面内极点关于原点的对称分布

应用劳斯判据还可以确定系统个别参数对系统稳定性的影响，以及判断系统特征方程根位于平行虚轴的直线（s＝－a）的左侧或右侧的数目。

［例4-08］ 单位负反馈系统的开环传递函数为G（s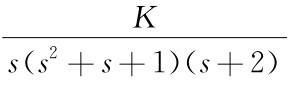）＝，试确定系统稳定的K。

［解］ 系统闭环传递函数为

可得系统特征方程为

s4＋3s3＋3s2＋2s＋K＝0

列劳斯阵列如下：

为使系统稳定，必须使劳斯阵列第一列元素为正，即K＞0，2－（9／7）K＞0。由此得系统稳定的K值范围为0＜K＜14／9。

［例4-09］ 设系统的特征方程s3＋7s2＋14s＋22＝0，试判断该系统有几个特征方程根位于与虚轴平行的直线s＝－1的右侧。

［解］ 令s＝z－1，代入特征方程，整理后得以z为变量的系统特征方程

z3＋4z2＋3z＋14＝0

再对此方程列劳斯阵列

由第一列元素二次变号可见，系统有两个特征方程根在平行于虚轴的直线s＝－1的右侧。

通过劳斯赫尔维茨判据可得出低阶系统稳定的充分必要条件如表4-1所示，在低阶系统判稳时可以直接采用表中的结论。

表4-1 低阶系统稳定的条件

劳斯 赫尔维茨判据根据系统特征方程的系数用解析方法来判断系统是否满足稳定的充分必要条件，对于开环系统、闭环系统以及由系统中部分环节组成的子系统（如系统中的小闭环部分）在判定稳定性时只要采用对应的特征方程。

劳斯判据不足之处是不能提供系统稳定程度的信息并建立定量指标来衡量系统稳定程度，但可以用来确定系统特征方程右根的数目，在Nquist判据（第5章）时有用到。