典型相关分析的数学实现

3.4.2　典型相关分析的数学实现

通过各种手段量测到的样品信息在数学上通常可以用矩阵的形式记录、表达。设对p个自变量X₁，…，X_p和q个因变量Y₁，…，Yq进行n次观测，p≤q，得到观测数据矩阵可表示为

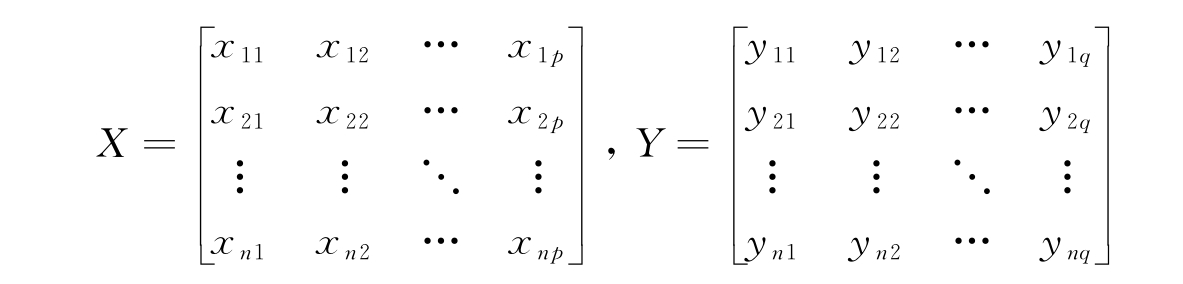
X，Y内部数据矩阵的各变量通常是不完全独立的，即有一些变量是相互依赖或相关的，从数学上来说就是这些测试数据矩阵X（Y）中存在相关的行或列。因而这两个数据矩阵可以由一些数量少于原来变量的、完全独立的新变量U_n×p，V_n×p重新表示（即进行降维），以消除原始变量间存在的相关性。更重要的是，新独立变量U，V能达到最大相关性，以充分反映两组指标间的相关信息。共p对典型变量，第k（1≤k≤p）对典型变量之间的相关系数称为第k个典型相关系数。

图3－5给出了典型相关分析的示意图：两类变量X与Y分别用新的一组典型变量U、V表示，U、V中的各元素分别为X、Y中变量的线性组合。CCA的目的就是求出这些线性组合中的系数，使得每一对典型变量U、V之间的相关系数CanR_i达到最大。

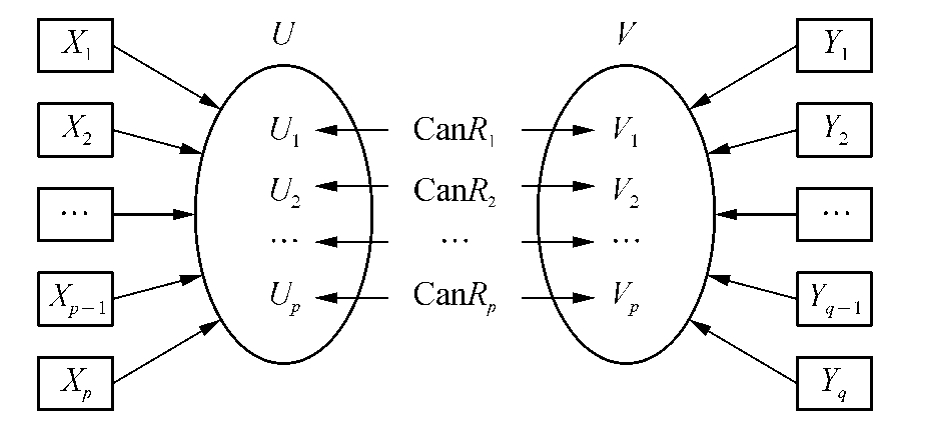
图3－5　典型相关分析示意图

典型相关分析的主要步骤如下。

1.求新变量（典型变量）的方差、协方差矩阵

典型变量U的方差Var（U）＝Var（α′X）＝α′R₁₁α（R₁₁为X的相关系数矩阵，维数为p×p）。

典型变量V的方差Var（V）＝Var（β′Y）＝β′R₂₂β（R₂₂为Y的相关系数矩阵，维数为q×q）。

典型变量U和V之间的协方差Cov（U，V）＝α′R₁₂β（R_12为X与Y的变量间的相关系数矩阵，维数为p×q）。

典型变量U和V之间的相关系数r_UV＝α′R₁₂β/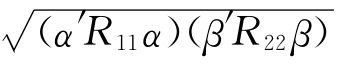

令M＝（X′，Y′）′，则

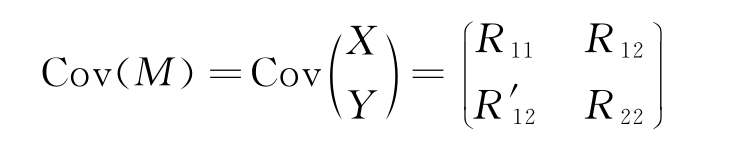
2.求矩阵A，B（即U、V变量表达式中的系数）

可以证明A，B具有相同的非零特征根，设为≥…≥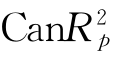，CanR是这两组随机变量相关关系的反映，即典型相关系数。

3.特征分解

式中，Λ为A，B的特征值组成的对角阵；α，β分别为A，B的特征向量按列组成的正交阵，它构成了新的矢量空间，作为新变量的坐标轴。

4.求典型变量U，V

最大特征值（第一典型相关系数）所对应的典型变量称为第一典型变量（U₁，V₁）。一般只取前几个影响大的典型变量和典型相关系数来分析。

5.典型变量回归

采用典型变量U，V代替原始变量X，Y进行多元线性回归分析则称为典型变量回归（Canonical Correlation Regression，CCR）。