3.1 简单线性相关分析
线性相关是指两个相关变量之间，当变量X的数值发生变动时，另一变量Y随之发生近似于固定比例的变动，在相关图上的散点近似地表现为直线形式，因此称其为线性相关关系。线性相关分析用于研究两个变量间线性相关的程度。任意两个随机变量X和Y间线性相互依存（关联）的程度可以用简单线性相关系数r（通常简称为相关系数）来描述。
例3－1 表3－1为某地区雨水中Na、Cl、Pb和Sb元素含量的测试数据。为考察雨水中Na与Cl，Pb与Sb含量间的关联度，分别以Na、Pb为横坐标、Cl与Sb为纵坐标，可得图3－1和图3－2的相关图。显然，雨水中Na和Cl的浓度具有较强的相关性，即Na含量上升时Cl含量也上升，但Pb与Sb的浓度不具备明显的规律和相关性。
表3－1 雨水中元素含量数据单位：ng·g－1
续表
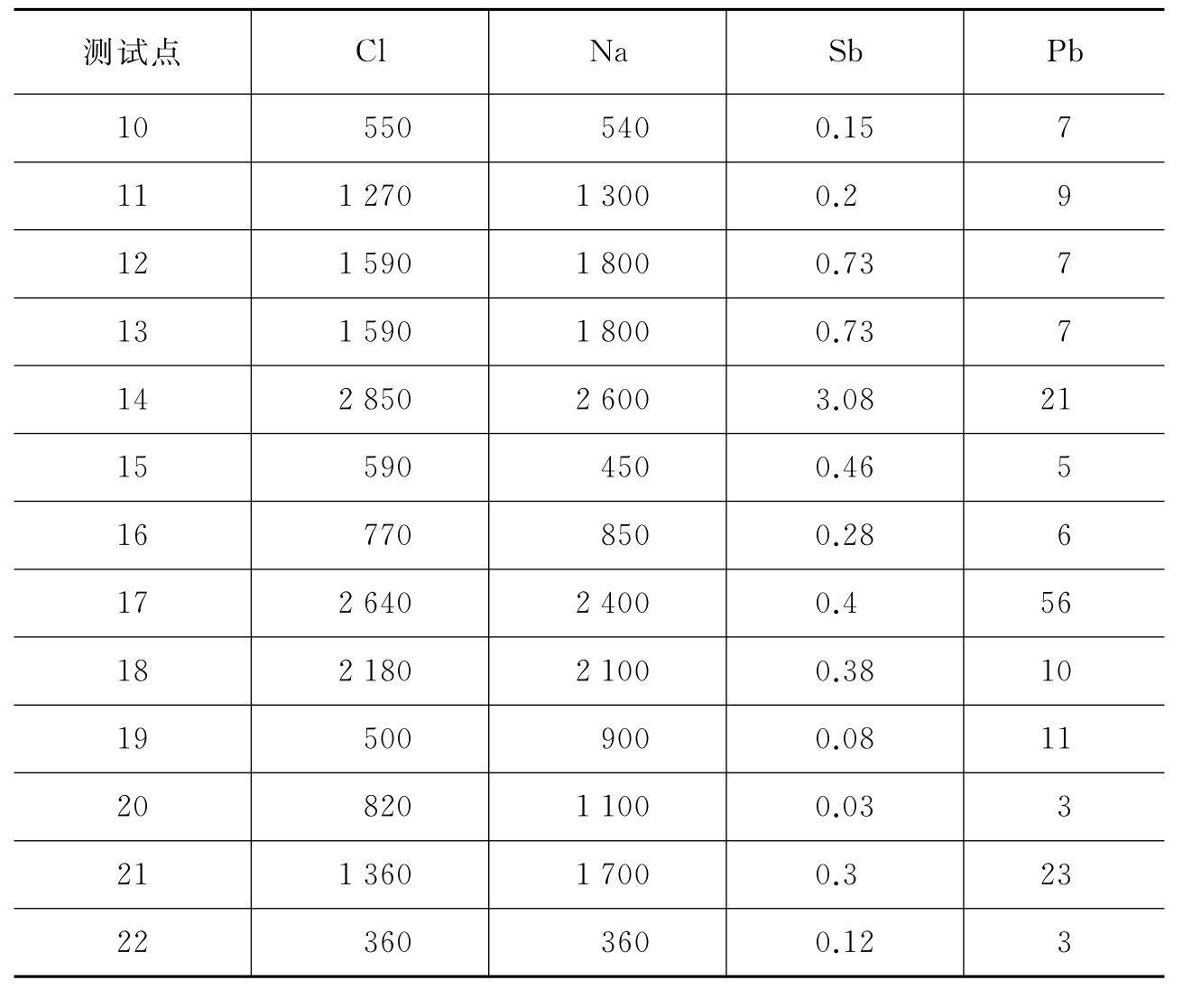
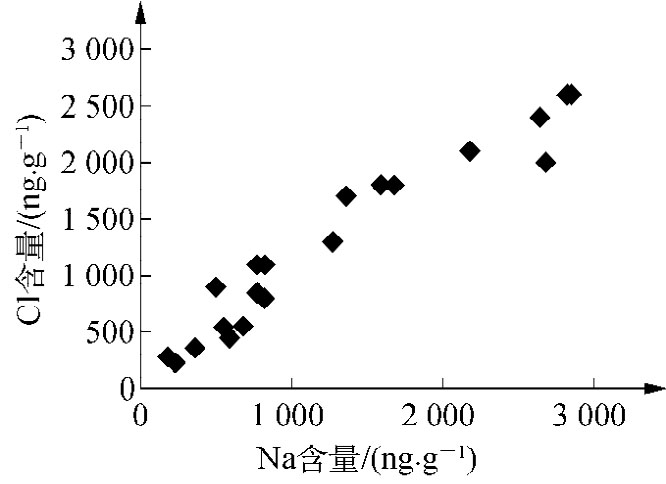
图3－1 雨水中Na与Cl浓度的相关图
图3－2 雨水中Pb与Sb浓度的相关图
变量间的相关性可以用协方差和相关系数来描述。
设X与Y的n次测量数据为Xi，Yi（i＝1，2，…，n），其均值分别为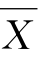
与
则变量X与Y的协方差可定义为
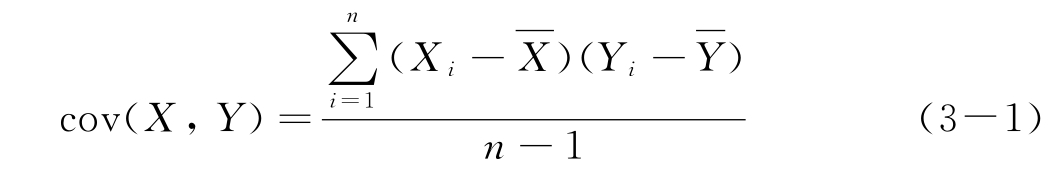
式中，n－1为独立观察次数，即自由度。
当变量X与Y之间的相关性较强时，协方差的绝对值将比较大；若变量X与Y的相关性较差时，协方差的绝对值将会比较小。此外协方差的大小还依赖于变量X和Y的量级，例如，上例中当Na与Cl的浓度单位为ng·g－1时，cov（Na，Cl）＝742 650，若Na与Cl的浓度单位为分别以μg·g－1表示时，则cov（Na，Cl）＝0.743。为了使相关性度量参数不依赖于变量所选用的量级（即单位）时，将协方差除以X和Y的标准方差的乘积，由此可得相关系数
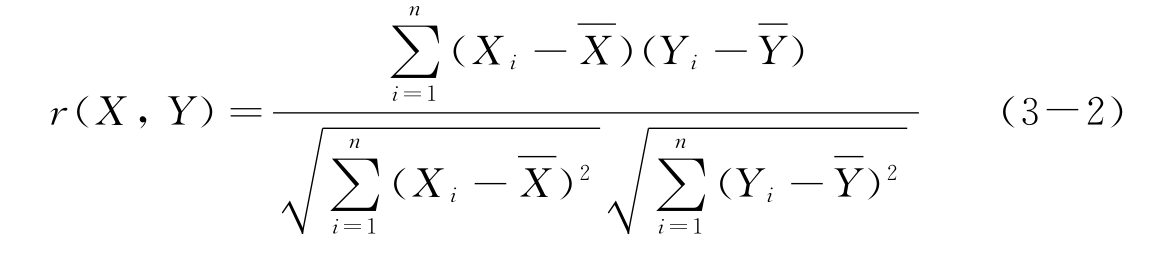
如果变量X和Y线性相关，如Y＝aX，此时式（3－1）可化为
式（3－2）化为
因此，对于线性相关的两个变量，其相关系数r＝1。
将表3－1中的第2～5列导入数据文件X，在MATLAB的command window下输入命令
＞＞R＝corrcoef（X）
%R＝corrcoef（X）计算数组X的相关系数矩阵R，X的每一列代表一个变量，每一行代表一个观察样本.
可以得到如下结果
R＝
R为表3－1中四个元素含量间相关系数构成的矩阵，如r（1，2）＝0.917 2表示雨水中Na与Cl含量间的相关系数为0.917 2；r（3，4）＝0.315 4表示雨水中Pb与Sb的含量间相关系数为0.315 4，这个值非常低，表现在图3－2中的点很分散，不像图3－1中的点比较集中地分布在一条直线附近，具有较强的线性相关性。
由式（3－2）可看出，在相关系数的概念里，用到了数理统计中均值、协方差、标准方差的概念：
与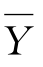
分别是变量X和Y的n次测试值的均值；分子
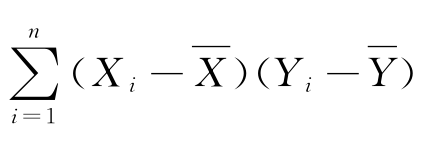若除以n－1即为变量X与Y之间的协方差；分母中的
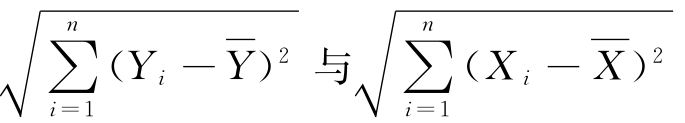若除以
则分别为变量X与Y的标准方差。因此可以说，X与Y的相关系数r等于其协方差与其标准方差之比。
当相关系数r＞0时，表明两个相关变量变化的方向是一致的，称这两个变量为正相关。如例3－1中Na与Cl的含量呈正相关关系。
若相关系数r＜0，则意味着两相关变量变化的方向是相反的，称这两个变量为负相关。
若｜r｜＝1，表明两个变量间完全线性相关，即二者之间存在完全确定的线性函数关系。
｜r｜＞0.95表明两个变量间显著线性相关。
｜r｜≥0.8表明两变量高度线性相关。
0.5≤｜r｜＜0.8表明两变量中度线性相关。
0.3≤｜r｜＜0.5表明两个变量的线性相关程度低。
｜r｜＜0.3表明两个变量的相关关系极弱，可认为无线性相关关系。
相对于线性相关变量，曲线相关是指变量X的数值发生变动时，另一变量Y也随之发生变动，但这种变动在数值上不成固定比例，在相关图上的散点可表现为抛物线、指数曲线、双曲线等形式，因此称其为曲线相关关系。
当两变量之间在数量的变化上各自独立、互不影响时，则称这两个变量不相关。注意，｜r｜＝0只意味着两个变量间没有线性相关关系，但并不一定意味着变量X与Y完全不相关。
图3－3给出了各种相关关系的示意图。
图3－3 各种相关关系示意
例3－2 表3－2给出了对某产品标明腐蚀刻线获得的腐蚀时间（x）与腐蚀深度（y）间的一组数据。试研究两变量（x，y）之间的线性相关程度。
表3－2 腐蚀时间与腐蚀深度的实验数据
解：在MATLAB命令窗口下输入
＞＞x＝［5 5 10 20 30 40 50 60 65 90 120］；
＞＞y＝［4 6 8 13 16 17 19 25 25 29 46］；
＞＞［R］＝corrcoef（x，y） %求向量X和Y的相关系数矩阵R
可以得到如下结果
R＝1.0000 0.9847
0.9847 1.0000
由此可知腐蚀时间x与腐蚀深度y之间的线性相关系数为0.984 7，说明这两个变量间的线性相关性很强，且呈正相关，即随着腐蚀时间的增加，刻蚀深度也增大。
在MATLAB命令窗口输入
＞＞plot（x，y，s）
可得到如图3－4所示的腐蚀时间（x）与腐蚀深度（y）之间的相关图，由此图可看出图中的点可以用一条直线（见图中的虚线）近似拟合，因此从两个变量数据点的直观分布也可以看出二者之间有显著的线性相关。
图3－4 腐蚀时间与腐蚀深度间的相关性
例3－3 一个混合溶液中有n个溶质，设每个溶质的质量为Mi、密度为ρi、浓度为ci，用变量M、ρ、c来描述溶液中的溶质，会得到一个n×3的矩阵X，矩阵X的每一行代表一个溶质的3个性质，每一列代表n个溶质对应的性质。
下面我们来求变量x1（质量M）与变量x3（浓度c）之间的相关系数。
由于ci＝Mi/V（V为溶液的体积），故n个溶质的平均浓度
由式（3－2）可知
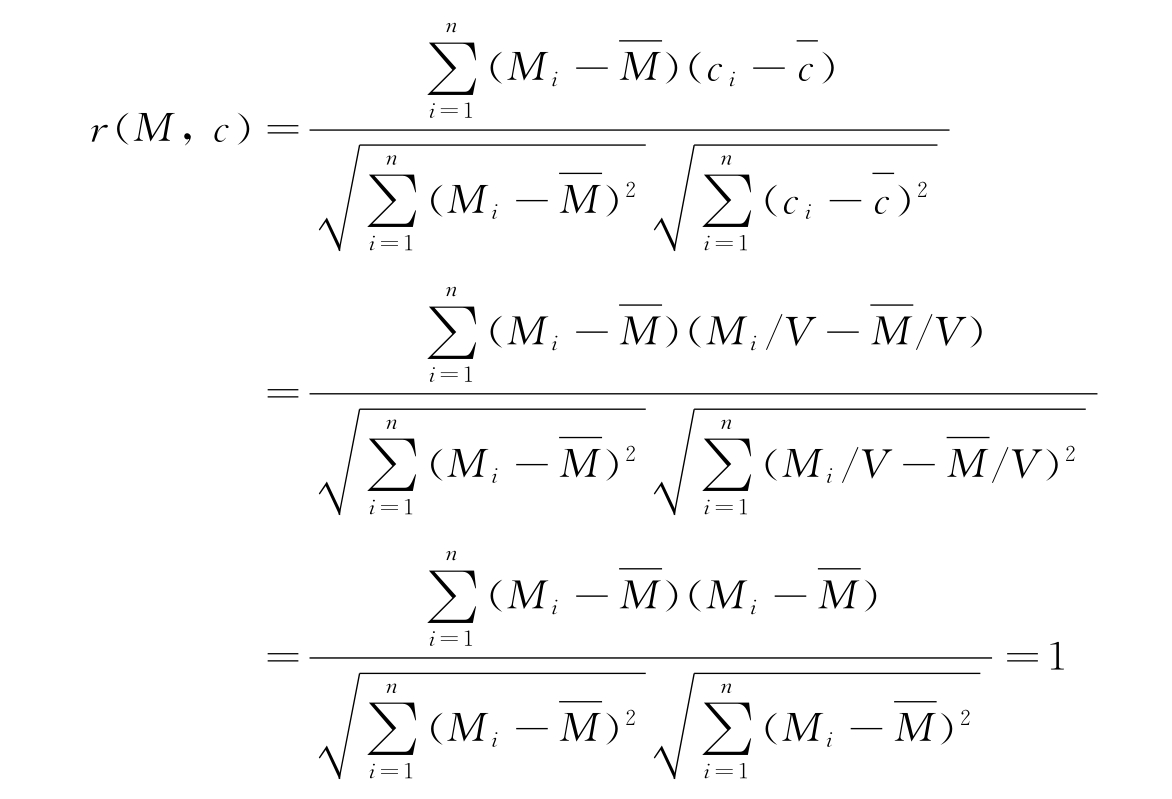
由此可见，由于浓度c与质量M成正比（在线性代数中称浓度c与质量M线性相关），使得二者之间的线性相关系数r＝1。在这种某一个变量可以由另一个（或几个）变量的线性组合表示的情况，意味着该变量不独立，其信息完全可以由其他变量体现，在数据矩阵中可以将这个变量所在的列去掉。
对于本例，溶质的浓度信息完全可以由其质量体现，故在描述溶质性质的变量中只要保留其中之一即可。变量的线性相关分析在后续的回归分析、模式识别中都非常有用，可以起到精简模型、提高模型性能的作用。
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
