不定方程概述

所谓不定方程一般指未知数个数多于方程个数，且对解有一定限制（比如要求解为正整数或整数、有理数等）的方程。它作为数论中的一个分支，内容极其丰富，而且有着悠久的历史。在第一章中，我们将对其做一个简单的概述性介绍。

在各文明古国的早期文化中，最早接触到的一类特殊不定方程是勾股方程。作为最古老的不定方程，勾股方程与我们所熟悉的勾股定理密切相关。勾股定理是说：在一个直角三角形中，斜边的平方等于两直角边的平方之和。

人类最早对勾股定理的认识往往与以整数为边的直角三角形（勾股形）联系在一起。现在我们一般把整边勾股形三边称为勾股数，也叫商高数，或按国外称法叫毕达哥拉斯数。比如，在我国《周髀算经》中有“勾广三，股修四，径隅五”，这就相当于给出了一组勾股数（3，4，5）。这也是各古代民族最早找到的一组勾股数。在我国《九章算术》一书“勾股章”中，使用了8组勾股数：（3，4，5）、（5，12，13）、（7，24，25）、（8，15，17）、（20，21，29）、（20，99，101）、（48，55，73）、（60，91，109）。古印度《测绳的法规》中出现了5组勾股数：（3，4，5）、（5，12，13）、（7，24，25）、（8，15，17）、（12，35，37）。

现在设x、y为两直角边的长，z为斜边的长，那么勾股定理可表示为：x2+y2=z2。如果把它看做一个代数方程，那么这个方程中含有三个未知数，而且出现了未知数的次数是二次的项，所以这是一个三元二次不定方程。这个不定方程就称为勾股方程。而勾股数则是满足勾股方程的正整数解。因此，可以说，当人类认识勾股数时，已经开始了对勾股方程的探讨。更进一步的研究是：找到可以一次产生许多勾股数的公式。

对此，古希腊的毕达哥拉斯学派得出一个结论：如果m是一个奇自然数，则m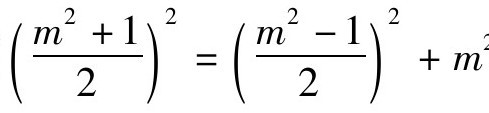，因此可以给出勾股方程的许多组解。

约公元前380年，古希腊著名哲学家柏拉图设计出另一公式：（m2+1）2=（m2-1）2+（2m）2，其中m为任意的自然数。于是，（m2-1，2m, m2+1）可以给出勾股方程的许多组解。

然而，这些公式却不能给出所有的勾股数。那么是否有公式能产生全部勾股数呢？换言之，能否找到勾股方程的通解公式呢？

可以证明，设m和n是两个正整数，m大于n, m、n互素且奇偶性不同，那么，m2-n2，2mn, m2+n2就可以给出全部基本勾股数。至于基本勾股数，是指三个数互素。显然，在基本勾股数的基础上，同乘以一个相同的倍数，就可以得出所有勾股数了。

能产生全部基本勾股数的公式在我国最早出现在《九章算术》勾股章中。在解第14题时，书中在（c+a）：b=m：n的题设下，以率的形式表示出了勾股形三边的关系：a：b：c=。如果加上“m>n>0，m, n同为奇数，且互素”的条件，则可以证明这一结果与上面的公式等价。不过，《九章算术》的术文未离开具体数字，刘徽则用出入相补原理对其一般形式作了证明。

在古印度，数学家婆罗摩笈多在《婆罗摩修正体系》（约628）中，也明确给出了勾股数一般解公式。在西方最先掌握全部解法则的数学家则是古希腊的丢番图。在他的名著《算术》中有若干处用到了这一公式，但丢番图在自己的书中没有明确表述出这一结论。

然而就现有的史料看，在勾股定理和勾股数方面，古巴比伦人取得的成就更为突出，并远远走在了其他文明古国的前面。

在发现的一些公元前1700年左右的古巴比伦泥板中已经有许多勾股定理的应用题，在这些题目中涉及了勾股数：（3，4，5）；（5，12，13）；（8，15，17）；（20，21，29）。古巴比伦人在勾股定理的认识上取得的最大的也是最令人惊叹的成就体现在一块长12.7厘米，宽8.8厘米的泥板中。这块泥板现珍藏在纽约哥伦比亚大学精品图书馆，编号为“普林顿322”（Plimpton 322）。经过鉴定，确认年代为公元前1900～前1600年。

最初人们以为这块泥板是古巴比伦人的一份商业记录，没有什么重要意义。1945年，一位巴比伦考古学家及数学家奥图·奈克包威尔（1899～1990）与他的助手做出了新的成功解释。他们撰文指出，泥板所记为勾股数。在这个实物证据中，共列出了15组勾股数。其中最大的一组斜边是18541，一个直角边是12709！其数之大和年代之早都令人难以置信。进一步的研究表明，古巴比伦人当时已经掌握了勾股方程的一般解公式，他们正是使用这一公式得出这些勾股数的。

不过，虽然古代人使用了勾股方程的通解公式，但从理论上证明这一公式确实能产生所有的基本勾股数却要晚得多。事实上，直到19世纪70年代这一证明才被做出。

除勾股方程外，最早被研究的是最简单的不定方程：二元一次不定方程。

二元一次不定方程的一般形式为：ax+by=c，其中a, b，c都是整数。稍进一步，可以研究更多元的一次不定方程，其一般形式为：a1x1+a2x2+……+anxn=N（其中a1，x2，……，an，N为整数，n≥2，a1，a2，……，a n均不为零）。对这一类不定方程，早在古代就已开始了研究，并得到了求解的方法。不过，古代的研究大多只限于找到算法。直到17世纪，法国数学家巴歇（1581～1638）才创立了一次不定方程的一般理论：得出了这类不定方程有解的充分必要条件，并在有解的情况下给出了求通解的一般方法。在第二章中，我们将比较详细地介绍求解二元一次不定方程的几种方法。这些方法各有独特之处，但却殊途同归，因为就本质而言它们都是利用了辗转相除法。

与一次不定方程相联的是一次不定方程组，其一般形式可表示为：

其中未知数的个数s大于方程的个数m。如果方程组右端的各常数项都为0，则称是齐次不定方程组。历史上最早的这类不定方程组来自我国的《九章算术》。

在此书方程章第13题提出了一个“五家共井”问题：“今有五家共井，甲2绠（绠是汲水桶上的绳索）不足如乙1绠，乙3绠不足如丙1绠，丙4绠不足如甲1绠，丁5绠不足如戊1绠，戊6绠不足如甲1绠。如各得所不足1绠，皆逮（达到的意思）。问井深绠长各几何？”

翻译成白话：“有五个家庭共同用一口井，他们分别用甲、乙、丙、丁、戊五根长短不一样的绳子汲水，甲绳2根连接起来还不够井深，短缺数刚好是乙绳的长。乙绳3根连接还不够井深，短缺数刚好是丙绳的长，丙绳4根连接还不够井深，短缺数刚好是丁绳的长，丁绳5根连接还不够井深，短缺数是戊绳的长，戊绳6根连接还不够井深，短缺数是甲绳的长。问井深、绳长各多少？”

我们设甲、乙、丙、丁、戊绳分别为x, y，z, s，t，设井深为u。于是根据题意，可得到下面的方程组：

这个方程组“五程六物”，即它包含有5个方程，6个未知数，因此是不定方程组。

通过求解，可以得到。

为了得到整数解，令u=721，则得x=265，y=191，z=148，s=129，t=76。

这恰好是书中给出的特解，即：井深7丈2尺1寸。甲、乙、丙、丁、戊五家汲水绳依此长2丈6尺5寸，1丈9尺1寸，1丈4尺8寸，1丈2尺9寸，7尺6寸。但这实际上只是给出了最小的一组正整数解。因为井深不确定，所以解并不唯一。刘徽在《九章算术注》中精辟地说：“举率以言之”，意思是说这些数据是在比的意义下说的。也就是说，方程组的解应是：x=265k, y=191k, z=148k, s=129k, t=76k, u=721k，而k是任意正数（当然，考虑实际情况，k的取值是有限制的）。

在国外，也出现过一些与“五家共井”问题相似，但在时间、方程个数，题目复杂程度上都逊于“五家共井”问题的例子。如古罗马人Metrodorus著《希腊箴言》一书第144题如下：

“石像A：我站立的基石和我共重多少？

石像B：我站立的基石和我与你与你的基石和同重。

石像A：我的重是你基石的2倍。

石像B：我的重是你基石的3倍。”

设石像A重x，石像A的基石重y，石像B重z，石像B的基石重u。那么根据题目条件可以得到不定方程组：

。这个方程组含有四个未知量，三个方程。易解得其一般解为：x=4k, y=k, z=3k, u=2k。

以上这类问题都归结为齐次不定方程组。对于齐次不定方程组来说，只是由于方程数目少于未知数的数量，所以最后得到的是不定解。对这类问题，可以通过消去法获解，是比较容易处理的一类不定方程问题。

复杂些的非齐次不定方程组问题也是我国最早提出的。出现在南北朝时期的《张丘建算经》中有著名的“百鸡问题”，它就可以转化为一个非齐次不定方程组。对这类一次不定方程组可用消元法化为一次不定方程求解。在第二章中，我们将对此做介绍。

除此外，我国古代在不定方程领域所做的研究还以对物不知数问题的深入探讨著称于世。这一问题出现在南北朝时期的《孙子算经》。在现代，这一问题被归为一次同余式问题。用大数学家高斯所引入的同余符号，它等价于求解满足下面同余式组的最小正整数N：。但如果设所求数为N, N除以3、5、7所得的商分别为x, y，z，那么这一问题又可表示为：。这是一个不定方程组问题。也就是说，物不知数问题，既是不定方程问题，也是同余式问题。上面给出的就是“不定方程组”和“同余式组”两种形异质同的“物不知数”问题的现代表达式。事实上，一次不定方程（组）与一次同余式（组）在本质上是相通的。两者可以看做是对同一问题的两种不同说法，彼此可以互化。

在古代中国，百鸡问题和物不知数问题作为典范，正好可以分别代表不定方程和同余式这两大研究传统，中国对这两种类型都做了比较早的研究。特别是在物不知数问题上，南宋数学家秦九韶在前人研究基础上，创立了著名的“大衍术”，比较圆满地解决了这一问题。我们将在第三章中详细介绍“物不知数”问题由提出到解决的历程。

古印度则更多的是研究不定方程，第一位知名的古印度数学家阿耶波多出于天文计算的需要曾热衷于寻求一个不定方程的所有整数解，并成功地创造了具有浓郁印度特色的“粉碎法”（梵语称“库塔卡”），开古印度一次不定方程研究之先河。

古印度在不定方程方面取得的更为非凡的成就则是求解佩尔方程。所谓佩尔方程是指形如x2-Ny2=1（其中N为正整数，且不是平方数）的不定方程。佩尔方程是二元二次不定方程中最简单的也是最重要的。至于N为正整数，且不是平方数的条件是为了保证此不定方程有非平凡解。比如，如果N为某一整数P的平方，则容易推得此方程只有平凡的整数解（1，0）和（-1，0）。

古印度数学家婆罗摩笈多在历史上最早对这类不定方程做了深入探讨，并得到了一种求解此类不定方程的方法，他的方法在随后被古印度数学家婆什迦罗所完善。在印度人之后，欧洲人于17世纪重新开始了对佩尔方程的研究。在花费了许多数学家的精力及上百年时间的努力后，法国数学家拉格朗日对此做出了完全而细致的分析，他的工作结果还涵盖了更一般的二元二次不定方程。其研究称得上是数论领域中的一项突出成就。在第四章中，我们将比较详细地介绍佩尔方程的求解方法及历史。

除古中国与古印度在不定方程方面的工作外，古希腊在不定方程的研究上也取得了重要的成就。这一成就主要来自于古希腊数学家丢番图。

在第一编中，我们已经介绍过丢番图及他在代数学方面的贡献。他在代数学发展上作出的贡献使他赢得了“代数学之父”的称号。除此外，丢番图在数论方面取得的突出成就也对后代产生了巨大影响。事实上，他划时代的《算术》一书虽包含了代数内容，具有代数学的特征，但更是一本数论著作。这书除了第一卷外，其余的问题几乎都是考虑不定方程问题。而它也以不定方程的求解而著称。

比如，在《算术》第二卷第20题，丢番图研究了这样一个问题：求两数，使得任一数的平方加上另一数等于一个平方数。用现代数学式子表示，这相当于求解不定方程：

与我们现在的做法不同，丢番图只设一个未知数，也只使用一个未知数的符号，其余的未知数则根据问题的具体条件用含此未知数的一个简单式子表示出来。以本题为例，设一个未知数为x，则由条件x2加上另一个未知数等于一个平方数，因此可设第二个未知数（即我们上面式子中的y）为2x+1。这样，第一个条件满足了，剩下的只是要求（2x+1）2+x也是平方数。为此，丢番图设（2x+1）2+x=（2x-2）2。解这一方程，可得到x=3/13，另一数则为19/13。

右端出现2x项显然是打算使展开后两边可以消去二次项，但-2是怎样来的？我们可以做出分析。假设右端是（2x+a）2，则展开对消后可得到，为得到正数解，即x>0，需要a<-1，或1<a<5/4。这样最简单的办法是令a=-2。当然通过这一分析，可以知道令a=-3等也是可以的。不过，丢番图的书中没有做这样的分析，他对自己这样设未知数的理由没有做出任何解释，更没有给出一般的法则。

再举一个丢番图研究过的题目。书的第二卷第8题，丢番图研究了：将一个已知的平方数分为两个平方数。用现代符号表示，问题相当于已知平方数z2，求数x, y，使得x2+y2=z2。

丢番图以z2=16为例说明了一下自己的解法。他先设一个平方数为x2，这样另一个就可设为16-x2，而问题变成要求16-x2是一个平方数。对此，丢番图设16-x2=（mx-4）2，其中m是任一整数，4是16的平方根。然后他取m=2，得到16-x2=（2x-4）2=4x2-16x+16，解得x=16/5。最后得到两个平方数：256/25，144/25。显然，这一问题还有其他解。但丢番图通常只给出问题的一个解就算完结。

丢番图所研究的这一问题在数学史上非常有名。原因是，当17世纪法国数学家费马阅读《算术》拉丁文译本时，在这个问题旁边的空白处写下了那条著名的旁注，从而引出了“下金蛋的鹅”——费马大定理。

为对丢番图所研究问题的深度与广度留下一个印象，我们下面再举几个丢番图研究过的有趣问题。

希腊文本卷3第10题：求三个数，使其中任何两数之和加上一已知数都为平方数。丢番图给出的答案是：2，2，1/8。

阿拉伯文本卷4第9题：求两个立方数，它们的积是一个平方数。丢番图给出的答案是：8和512。

希腊文本卷5第9题：将1分为两部分，使同一个已知数加到任一部分上，结果都是平方数。丢番图给出的答案是：4843/10201，5358/10201。

希腊文本卷6第21题：求一直角三角形，使其周长是一个平方数，而周长加上面积是一个立方数。丢番图给出的答案是：1024/217，215055/47089，309233/47089。

《算术》中类似的题目还很多，在解决这些问题时，丢番图显示出其高度的巧思。他关于不定方程的一些巧妙解答，往往使人眼花缭乱、叹为观止。作为一位有高超技巧的解题能手，丢番图在多方面显示出惊人的睿智和独创性。这使《算术》一书成为具有高度创造性的伟大著作，并对欧洲的数论产生了深远的影响。为了纪念丢番图对不定方程所作的广泛而深入的研究，现在通常把不定方程叫丢番图方程，求整系数不定方程的整数解被称为丢番图分析，而由求解不定方程发展起来的当代两大先进手段也被称为丢番图逼近和丢番图几何。

但丢番图《算术》一书也存在一些缺陷。其中最大的问题是书中只反复讲述为每一个特殊问题的需要而设计的巧妙方法，缺少一般方法。对此，数学史家韩克尔（1839～1873）曾评论说：“近代数学家研究丢番图的100个问题后，想去解第101道题，仍然感到困难。丢番图使人眼花缭乱，甚于使人神怡心悦。”妨碍他取得普遍性方法的重要原因在于其符号体系不完美。首先，他只用一个符号表示未知数，遇到多个未知数时，不得不用“第一个、第二个、第三个……”或“大的、中的、小的……”等词句去表达。在多数的情况下他令那些未知数取得具体的数值，于是使问题特殊化而得不到普遍的解答。其次，没有创用符号去表示已知量（如现在的a, b，c），因此其所有的解法都是针对具体数字而设的，对一般的数就不一定适合，这样当然得不到一般的解法。

另外，与上面所举例子类似，丢番图在解决其他问题时，虽然知道题目有多个答案，但在多数情况下，他满足于对一个问题只求出一个解。而且，他的答案要求是正有理数。这与现在不定方程的解一般要求是整数也有差别。

与古中国、古印度研究的是一次或二次不定方程不同，丢番图研究的主要是高次不定方程，其中包括后来被称为椭圆方程（曲线）的不定方程。

椭圆方程的较简单形式是：y2=x3+k，其中k是整数。在丢番图之后，法国数学家费马又重拾这类问题。1657年，费马在向其他数学家挑战时提出问题：证明26是仅有的夹在一个平方数和一个立方数之间的数。这等价于证明椭圆方程y2=x3-2只有一个解（3，5）。费马自称自己发现了这一问题的一个美妙而精巧的方法。但他的证明生前一直没有发表，去世后也始终没有被发现。事实上，证明这一结论是相当困难的事情。直到1875年，一位数学家才给出了一个完全的证明。

椭圆方程更一般的形式是：y2=x3+ax2+bx+c, a，b, c是任何整数。但因为用比较简单的代数运算，可以把这种形式的方程转换成其中没有x2次项的方程。因此，研究椭圆方程，只要考察形如y2=x3+ax+b的方程即可，它已包含了所有的情形。与一次、二次不定方程的研究不同，人们对椭圆曲线的有理数解与整数解都感兴趣。

对此类方程解的性质的研究引出一大堆课题。自费马之后，许多数学家对这类不定方程做了研究，他们运用各种方法研究它的整数解或有理数解。20世纪，数学家莫德尔首先在这方面得到许多重要成果。

莫德尔（1888～1972），著名的数论家和丢番图分析专家。他出生在美国费城，在那儿度过了他生命的前18年。莫德尔后来曾在许多场合回忆自己对数学兴趣的开端：

大约14岁进入高中之前，莫德尔在费城有名的里尔书店的5美分和10美分特价书柜台偶然看到了一些旧的代数书。不知什么原因，这个学科吸引了他。其中一本书是哈克雷的《论代数》，作者是当时纽约市哥伦比亚学院的教授。他看到的是1849年第三版。这本好书，虽然不太严密，但包含了大量的材料，包括方程理论、级数和一章数论。同那个时代的老代数学一样，这本书有一章讲丢番图分析，这是他最感兴趣的主题。他后来的许多最好的研究都是关于这个主题的，不能说和它没有关系。

莫德尔后来去了英国，并在英国度过了大多数职业时间。1912年，他由于给出椭圆方程y2=x3+k的一系列新结果，而获得英国剑桥大学颁发的史密斯奖。1918年，他证明了方程y2=x3+k仅有有限组整数解。莫德尔也对更一般的椭圆方程做了深入研究。1922年，他给出并证明了著名的莫德尔定理。通过这一定理，人们可以从两个已知的有理解出发，反复应用一种算法，得出越来越多的有理解。同时，莫德尔提出了著名的莫德尔猜想：任一个不可约的有理系数的二元多项式，当它的亏数大于或等于2时，最多只有有限个解。这一猜想也被表述为：在亏格大于1的代数曲线上仅有有限个有理点。这个涉及不定方程理论的基本问题吸引和刺激了许多数学家，并激发出一系列的研究工作。1983年，29岁的德国数学家法尔廷斯（1954～）在前人工作基础上，最终证明了莫德尔猜想。这一证明被誉为20世纪数论中最杰出的工作之一。作为这一结果的推论，可以得出费马方程xn+yn=zn（n>2）仅有有限组非平凡解。这曾是费马大定理研究中一项重大突破。

由于在椭圆方程上所做的贡献，y2=x3+k这类方程也被称为莫德尔方程。在这方面的另一重要结果由德国数学家西格尔（1896～1981）做出。1926年他证明了结果：椭圆曲线y2=x3+ax2+bx+c上只有有限个整点。

椭圆曲线与一次、二次不定方程的研究不同，对后者，改变方程中的系数基本不影响求解。事实上，人们对它们已经有了统一的、有效的方法求解。因此，可以说现在人们对它们已经透彻地了解了。然而，对前者，通过简单地改变一般椭圆方程中a, b，c的值，则可以产生无穷多种方程，而且每一种都有自己的特性。比如说，对y2=x3+17，1930年数学家内格尔证明了它有8组解。而对y2=x3+7与y2=x3-15，则直到1963年才被完全解决。这一特点使得椭圆曲线的研究困难得多。即便到现在，椭圆方程依然有着许多艰难的问题要研究。“要完全理解它们还差得很远。对那些仍然未解出的椭圆方程，我仍能够提出许多表面上看来简单的问题。甚至费马本人考虑过的一些问题，至今也未解决。所有我完成的数学工作，在某些方面都可以追溯到费马，并不只是费马大定理。”——成功证明费马大定理的英国数学家怀尔斯如是说。

椭圆曲线不仅困难，而且其重要性也越来越明显。自20世纪50年代初以来，数学家清楚认识到，椭圆曲线是重要的基础性数学对象，它们与数学的许多领域，包括数论、几何学、密码学等都有联系。一个可以说明椭圆曲线重要性的例证是：1994年，怀尔斯通过证明一个关于椭圆曲线的结果而证明了费马大定理。

在椭圆曲线这里，我们还可以充分体会到不定方程与确定方程的一个大差别：确定方程有一套明确的解法，每一类方程都有固定的方法求解，不定方程则花样翻新。你会解一个不定方程，不一定会解同类方程。这正是不定方程问题往往非常困难的原因所在。

“只要一门科学分支能提出大量的问题，它就充满着生命力；而问题缺乏则预示着独立发展的衰亡或中止。”

在不定方程的研究中，人们永远不必担心问题的缺乏，而且数不尽的问题解决起来往往都非常困难。事实上，当前除一次不定方程、二次不定方程及某些高次方程的求解问题已解决外，绝大多数不定方程的求解无一定的规律可循，往往需要因题而论。可以说，对于高于二次的多元不定方程，人们迄今知道得还不多。另一方面，不定方程现在已与数学的许多分支（如代数数论、代数几何、组合数学等）建立起紧密的联系。这些都使不定方程这一古老的分支继续吸引着许多数学家的注意，成为现在数论中重要的研究课题之一。

对古代人来说，他们关注的一般只是对某不定方程找到求解的一种算法，而很少涉及对此不定方程的理论探讨。现在则不同。对于任何不定方程或方程组，人们都要研究如下几方面的问题：（1）解的存在性问题：找到一个判别方法，判断该不定方程是有解还是无解。（2）解的数目，即有解时确定解的个数。这有三种情形：只有平凡解；有限多非平凡解；无穷多非平凡解。（3）解的完全组，即把所有的解找出来。如果丢番图方程只有有限多解，我们希望具体把解都列出来。如果有无穷多解，我们希望用公式把解表示出来，其中关键的一步是要证明除了列举的解之外再没有其他的解。

对于不定方程，能够获得“解的完全组”如此满意的结果是不多的，只有勾股方程、一次不定方程、佩尔方程等少数方程。对更多的不定方程人们只有满足于探讨解的大小：在知道解为有限，或不能确定只有有限多解时，往往通过丢番图逼近的方法对于解的大小进行估计，特别是希望能够得到一个解的大小的上界。

事实上，一般来说，即便决定一个不定方程有没有整数解，也绝非易事，其复杂性由所谓希尔伯特第十问题及其解决的过程可略见一斑。1900年，德国大数学家希尔伯特提出了著名的23个数学问题。其中第10个问题是：给定一个具有任意多个未知数的整系数丢番图方程，是否可以找到一种算法，使得借助它，通过有穷次运算可以判定该方程有无整数解？在经过70年众多数学家的共同努力下，这一问题在1970年得到否定的答案。在第五章我们将对此过程做一简要介绍。