正项级数收敛性的判别法

通项都是正的级数称为正项级数。对于正项级数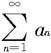作出它的相应部分和数列：

S₁＝a₁，S₂＝a₁＋a₂，…，S_n＝a₁＋a₂＋…＋a_n，…．

由a_n的正性，有

S_n≤S_n＋1．

从而，｛S_n｝是单调递增数列。由数列的单调收敛定理有以下定理。

定理7.2.1　正项级数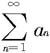收敛的充分必要条件是其部分和数列有界，即有正数M，使对一切自然数n成立

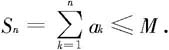
若部分和无界，则正项级数发散至正无穷。

从定理7.2.1出发，容易证明如下的定理：

定理7.2.2—1（比较判别法）　考虑正项级数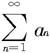和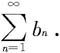假设存在自然数N，使当n＞N时，总有

a_n≤b_n．

（i）若级数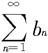收敛，则级数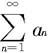也收敛；

（ii）若级数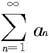发散，则级数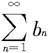也发散。

证明　（i）因为改变级数有限项，不影响原有级数的收敛性，因此不妨设对所有n都有a_n≤b_n，现分别以A_n和B_n表示级数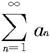和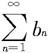的前n项部分和，则

A_n≤B_n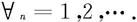

当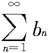收敛时，若令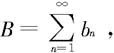则

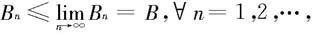
从而对一切n

A_n≤B．

由定理7.2.1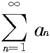，收敛。

（ii）用反证法。若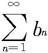收敛，由（i）得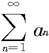也收敛。这与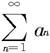发散矛盾，从而得证。　　□

在实际应用时，下面的极限形式往往是方便的。

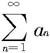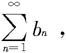定理7.2.2—2（比较判别法的极限形式）　考虑正项级数和假设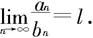

（i）若0＜ι＜+∞，则两个级数同时敛散；

（ii）若ι＝0，级数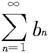收敛，则级数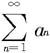也收敛；

（iii）若ι＝+∞，级数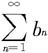发散，则级数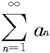也发散。

证明　（i）当0＜ι＜+∞时，取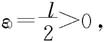由条件知存在自然数N，使当n＞N，就有

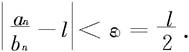
这等价于

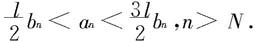
再由定理7.2.2—1即知所说的两个级数同时敛散。

（ii）和（iii）的证明是类似的。　　□

注意在（ii）中，即使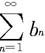不收敛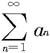，也可能收敛。在（iii）中，即使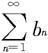不发散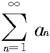，也可能发散。

例7.2.3　假设p＞0，讨论级数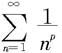的敛散性。

解　由上节例7.1.4知，所论级数在p＝1时发散。从而由比较判别法知当0＜p≤1时级数发散。下面讨论当1＜p＜+∞时级数的收敛性，由于p＞1时，

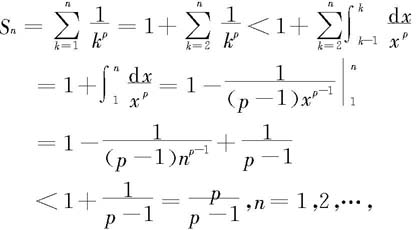
即｛S_n｝有界。由定理7.2.1知所论级数当p＞1时收敛。　　◇

综上所述，所论级数当p＞1时收敛，而当0＜p≤1时发散。

例7.2.4　判断级数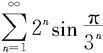的收敛性。

解　因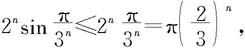而级数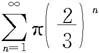收敛，所以该级数收敛。　　◇

例7.2.5　判断级数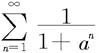（a＞0）的敛散性。

解　当0＜a≤1时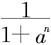，不趋于零。因而，此时级数发散。当a＞1时，因

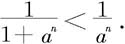
而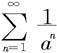收敛，从而由比较判别法知级数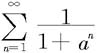收敛。　◇

例7.2.6　判断级数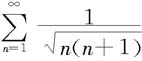的敛散性。

解　由于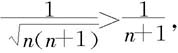而由例7.2.3知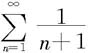发散，从而由比较判别法得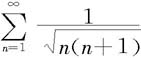发散。　　◇

例7.2.7　判断级数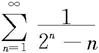的敛散性。

解　因为

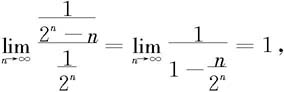
而几何级数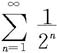收敛，故由比较判别法知级数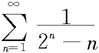收敛。　　◇

例7.2.8　设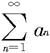和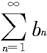都是正项级数。若从某一项以后（如n＞N），不等式

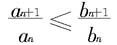
成立，则有

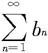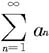（i）若收敛，则也收敛；

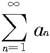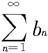（ii）若发散，则也发散。

证明　不失一般性，可以认为上述不等式对所有n＝1，2，3，…成立，此时易见

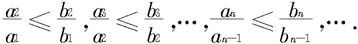
把它们两边各自相乘可得

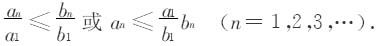
由比较判别法即知定理结论成立。　　◇

定理7.2.9—1（D'Alembert（达朗贝尔）判别法，也称为比值判别法）　设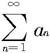是一个正项级数，记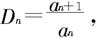n＝1，2，3，…，则有

（i）若存在0＜q＜1及自然数N，使当n≥N时有D_n≤q，则级数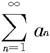收敛；

（ii）若存在自然数N，使当n≥N时D_n≥1，则级数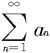发散。

证明　（i）由假设，当n≥N时D_n≤q，故有

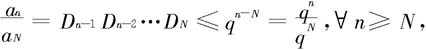
从而，

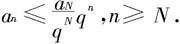
因为0＜q＜1，几何级数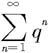收敛，故由比较判别法知级数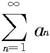收敛。

（ii）因为当n≥N时D_n≥1，故当n＞N时有

a_n≥a_n－1≥…≥a_N＞0．

所以不可能有a_n→0（n→∞），由上节定理7.1.7知级数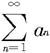发散。　　□

定理7.2.9—2（比值判别法的极限形式）　设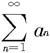是一个正项级数，记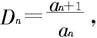n＝1，2，3，…

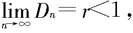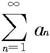（i）若则级数收敛；

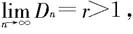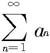（ii）若则级数发散。

证明　（i）取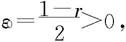因为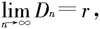故有N，使当n＞N时，就有

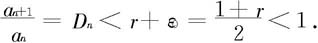
由定理7.2.9—1之（i）知级数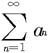收敛，即（i）成立。类似可证（ii）成立。　　□

例7.2.10　讨论级数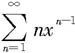（x＞0）的收敛性。

解　因为

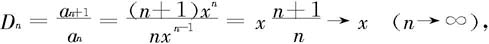
由定理7.2.9—2，当0＜x＜1时，级数是收敛的；当x＞1时，级数是发散的；当x＝1时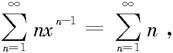，显然，此时级数发散。　◇

定理7.2.11—1（Cauchy判别法，也称为根式判别法）　设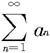是一个正项级数，记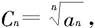n＝1，2，3，…，则有

（i）若存在0＜q＜1及自然数N，使当n≥N时有C_n≤q，则级数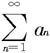收敛；

（ii）若存在自然数列的子列n_i，使得C_ni≥1，则级数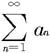发散。

证明　先证（ii）。当C_ni≥1时有a_ni≥1，故这时级数的通项不能趋于零，级数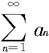当然是发散的。

（i）按已知有N，当n＞N时有

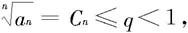
所以有

a_n≤qⁿ，n≥N．

因几何级数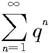收敛，故由比较判别法知级数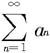收敛。　□

定理7.2.11—2（根式判别法的极限形式）　设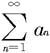是一个正项级数，记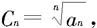n＝1，2，…

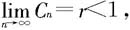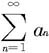（i）若则级数收敛；

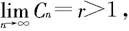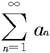（ii）若则级数发散。

按极限定义再利用定理7.2.11—1即可证明（i）和（ii），这里从略。

例7.2.12　判断级数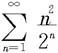的收敛性。

解　由于

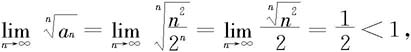
则由根式判别法知该级数收敛。　　◇

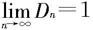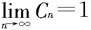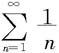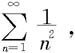注意　在比值判别法和根式判别法的极限形式中，对r＝1的情形都未论及。实际上，当或时，无法使用这两个判别法来判别敛散性。例如上节中的两个级数和都有

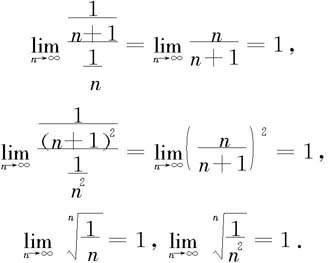
但前者发散而后者收敛。

注意　定理7.2.9—1和定理7.2.11—1中关于收敛的条件D_n≤q＜1和C_n≤q＜1也不能放宽成D_n＜1和C_n＜1。例如，对于调和级数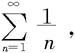有

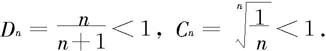
但级数都是发散的。

我们在例7.2.3中所使用的将级数的部分和化为积分来处理的方法具有一般性，这就是如下的：

定理7.2.13（积分判别法）　设函数f（x）在区间［1,+∞）上恒正且递减，A_n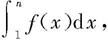＝n＝1，2，…，则级数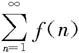与数列｛A_n｝同时敛散。

证明　由条件和定积分性质有

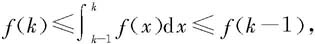
对k从2到n求和，得到

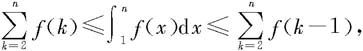
若记级数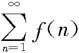的部分和为S_n，则上式化为

S_n－f（1）≤A_n≤S_n－1．

按定义知级数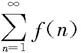与数列｛A_n｝同时敛散。　□

例7.2.14　讨论级数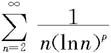（p＞0）的敛散性。

解　当p＝1时，因为

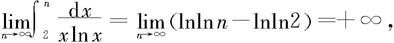
故由积分判别法知所论级数发散。再由比较判别法知所论级数于p≤1时发散。

当p＞1时，因为

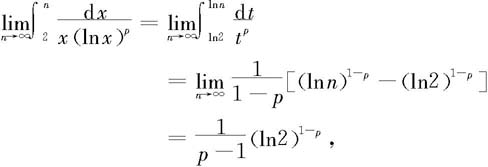
所以由积分判别法知所论级数收敛。

综上可知，级数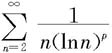于p＞1时收敛，而于0＜p≤1时发散。　　◇