其他数字特征

一个随机变量的数学期望、方差、标准差和两个随机变量的协方差、相关系数是最常见的一些数字特征。下面我们将介绍另外几种数字特征，它们在概率统计中的有些场合也有不少应用和一定的价值。

（一）矩（moment）

定义4.4.1　设X，Y为随机变量，k，l为正整数，如果以下的数学期望都存在，则称

为X的k阶（原点）矩。称

为X的k阶中心矩。称

为X和Y的k＋l阶混合（原点）矩。称

为X和Y的k＋l阶混合中心矩。

显然，随机变量的期望即为其一阶原点矩，而随机变量的一阶中心矩恒为0，方差即为二阶中心矩。而协方差Cov（X，Y）就是X与Y的二阶混合中心矩。在数理统计的参数估计中，我们将利用矩进行一些应用。

（二）分位数（quantile）

定义4.4.2　设连续型随机变量的分布函数和密度函数分别为F（x）与f（x），对任意的O<α<1，称满足条件

的实数为随机变量X（或此分布）的上（侧）α分位数（或上侧α分位点）。

图4.4.1

从几何角度来看，是把密度函数以下，x轴以上的区域分为两块，其右侧部分的面积恰好是α。见图4.4.1。

特别地，当α＝1/2时，称为X的中位数；当α＝1/4时，称为X的上1/4分位数；当α＝3/4时，称为X的上3/4分位数。

易见随机变量的上α分位数可以表示概率分布的特征，如：中位数的作用与前面介绍过的期望类似，刻画了分布的中心位置；而若想刻画分布的离散情况，也可以用两个不同分位数之差来表示，如：。

例4.4.1　由习题四第3题知柯西分布的期望不存在，但是由于其密度函数

是关于x＝0对称的，且对任意的，所以柯西分布的中位数存在且为0。

例4.4.2　标准正态的上（侧））α分位数通常记为，即是满足条件

的实数，其中φ（x）是标准正态的概率密度函数。根据附表2，可以得到以下一些常用的值：

另外由于φ（x）关于x＝0轴的对称性，可知

且。

例4.4.3　假设X～N（0，1），在Excel中求正态分布的分位数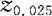，具体如下；在Excel表单的任一单元格输入“＝”在主菜单中点击“插入”“函数（F）”在选择类别的下拉式菜单中选择“统计”选择“NORMINV”点击“确定”在函数参数表单中输入，然后“确定”即在单元格中出现“1.959963985”。按上面的分位数的定义，Excel给出的是P（X>1.959963985）＝0.025，即Z0.025＝1.959963985。

在实际应用中，中位数是很常用的一个数字特征，特别是在社会统计中，常用之来刻画某种量的代表性数值。与期望相比较，中位数的一大优点是，它总是存在的，而且受个别特别大或者特别小的值的影响很小，而期望则依赖于所有可能取值。例如：在一个5人的团体中，有一个是超过2米10的高个子，而其他人都是中等身材，那么该团体的身高的平均值就可能比较高，因此这个均值就不具太大的代表性，中位数则几乎不受这些“异常点”的影响，稳健性好。但是中位数也存在其不足：数学上的处理不够方便，一般都只能从定义出发去寻找，而不如期望有很好的性质可以利用，而且中位数不一定具有唯一性，有时这也会给应用上带来一些困扰。

（三）众数（mode）

除了期望、中位数外，还可以用“众数”来表示随机变量的中心位置。

定义4.4.3　随机变量X最有可能取的数值，称为众数，记为Mo（X）。

易见，众数不一定具有唯一性。比如，对于离散型随机变量，众数则是其分布律中最大概率所对应的那个变量可能取值。

例4.4.4　设随机变量X服从参数为（n，p）的二项分布，求Mo（X）。

解　记。则

由此可见，随着k的增大，的值先增后减。若（n＋l）p为整数时，达到最大，则（n＋1）p与（n＋1）p－1是众数；若（n＋1）p不为整数时，记其整数部分为，则当k<m和k>m时，都有，因此［（n＋1）p］是众数。即

一般而言，数学期望、中位数、众数不一定相等，但在一些特殊情形下，三者也有可能完全一样（如：正态分布），