问题的解答

问题的解答

现在我们就可以来回答第一节中的问题了。

结论2：

现有N个小球，其中有一个坏球不知比标准球轻还是重。我们令H＝｛log₃2N｝。

（1）要保证在N个球中找出坏球并知道其轻重，至少需要称H次。

假设N≠2，我们有：

（2）如果N＜（3^H-1）／2，那么称H次就足够了；

（3）如果N＝（3^H-1）／2，那么称H次足以保证找到坏球，但不足以保证知道坏球比标准球轻还是重；

（4）如果N＝（3^H-1）／2，而且还另有一个标准球，那么称H次足以保证找到坏球和知道，知道坏球比标准球轻还是重。

假设N＝2，我们有：

（5）如果还另外存在一个标准球，那么只要称H＝｛log₃（2×2）｝＝2次足以保证找到坏球和知道坏球比标准球轻还是重。

（5）看起来有点奇怪，不过这其实很显然。如果有超过两个球，我们知道坏球是“独一无二”的那一个，总找得出来；但是如果只有两个球，一个好球一个坏球，都是“独一无二”的，如果没有一个标准球的话，我们无论如何不可能知道哪个才是好的。

首先假设结论成立，我们来看看几个具体例子。如果是12个球，那么

H＝｛log₃（2×12）｝＝3，

而且

12＜（3³-1）／2＝13。

所以根据2）我们知道称3次可以找出坏球并知其轻重。如果是13个球，那么

H＝｛log₃（2×13）｝＝3，

而且

（33-1）／2＝13。

根据3）我们知道称3次可以找出坏球但不一定能知其轻重。但是如果另有一个标准球的话，称3次就可找出坏球且知其轻重。

一般地，能由H次称量找出坏球并知道其轻重的最大小球数量为

（3^H-1）／2-1＝（3^H-3）／2；

能由H次称量找出坏球但不需要知道其轻重的最大小球数量为（3^H-1）／2；

有一标准球，能由H次称量找出坏球并知道其轻重的最大小球数量也为（3^H-1）／2。

为了比如说为了找出坏球并知道其轻重，则3次最多可以称12个，4次为39个，5次为120个，6次为363个等等；为了找出坏球却不需知道其轻重，则3次最多可以称13个，4次为40个，5次121个，6次364个等等——但是如果另有一个标准球，那么就可以用相同的次数来知道坏球的轻重。

首先我们证明至少需要称｛log₃（2N）｝次。这和上节类似问题的证明几乎相同。我们看到，N个小球可能的布局是2N种（1重，2重，……，N重，1轻，2轻，……，N轻）。所以相应策略树至少需要有2N片叶子。但是一棵高度为H的三分树最多只能有3^H片叶子。于是这棵策略树必须满足条件

H≥｛log₃2N｝

现在我们来证明3）的后半部分：如果N＝（3^H-1）／2，那么称H次还是不足以保证知道坏球比标准球轻还是重。

我们知道第一步称量一定是各放n（这里2n≤N）个球在天平两端，然后看天平的状况再决定后面的步骤。此时有三种情况

（1）如果天平平衡，那么坏球就在剩下的N-2n个球里。这时候根据1），我们还需要｛log₃2（N-2n）｝次来找到坏球并知其轻重；

（2）如果是左边重，则要么是坏球比较轻，而且坏球在右面n个球里，要么是坏球比较重，而且坏球在左面n个球里。这时根据结论1，我们还要｛log₃2n｝次来找到坏球并知其轻重；

（3）如果是右边重，那么有和上面类似的结论，我们还要｛log₃2n｝次来找到坏球并知其轻重。

如果我们在H次里可以称出坏球并知其轻重，那么我们必然要有

｛log₃2（N-2n）｝≤H-1和｛log₃2n｝≤H-1

但前一个式子表明

2（N-2n）≤3^H-1

也就是

2（（3^H-1）／2-2n）≤3^H-1

所以

3^H-1≤2n＋1／2

考虑到3^H-1为整数，于是

3^H-1≤2n

但3^H-1又是奇数，而2n是偶数，所以

3^H-1＜2n。（＊）

而后一个式子表明

2n≤3^H-1

同样考虑到奇偶性

2n＜3^H-1。（＊＊）

我们看到（＊）和（＊＊）式是矛盾的。

所以对N＝（3^H-1）／2的情况，只用H步是不能够称出坏球又知道它的轻重的。它的原因在于，虽然理论上N＝（3^H-1）／2，那么可能的布局是（3^H-1）种，而一棵H层的策略树有3^H片叶子，看起来叶子足够多了。但是由于第一步的称量无论如何也不可能把这3^H-1种布局平均地分配在左中右三棵子策略树上，总有一个分支上承受的布局会超过3^H-1种，于是在此分支上就无法用剩下的H-1次称量来称出坏球又知道它的轻重。

接下来我们同时证明结论2中的（2）、（4）和（5）。也就是说，我们要具体找到一种策略，如果N＜（3^H-1）／2，那么不用标准球在H次内找到坏球又知道它的轻重的；如果N＝（3^H-1）／2或者N＝2，则允许使用一个标准球来达到同样目的。仍旧使用数学归纳法。

首先对N＝1，｛log₃2N｝＝1且N＝（31-1）／2，允许使用标准球。因为只有一个球，而题目的条件是有一个坏球，所以这唯一的一个就是坏球，现在只需要知道它比标准球重还是轻。这只要把标准球和这个小球在天平上比较一次就可以了，策略树如下（我们用s表示标准球）：

对N＝2和N＝3，｛log₃（2N）｝＝2。我们给出下面高度为2的策略树，很容易验证其正确性。

N＝2，允许使用标准球：

现在假设对小于N的情况，称法都已经找到。考虑N（现在假定N＞3）个小球的情况。

仍记H＝｛log₃2N｝。

首先如果N＜（3^H-1）／2，我们把N个球分成三堆：第一堆和第二堆中分别有｛N／3｝个球，第三堆中为剩下的球，有N-2｛N／3｝个。

我们把第一和第二堆小球放在天平左右端进行第一次称量。

三种情况：

如果天平平衡，那么坏球在第三堆的N-2｛N／3｝个里，问题归结为N-2｛N／3｝个小球，称H-1次，而且此时我们可以随便从第一或第二堆里拿出一个球来作标准球。但是

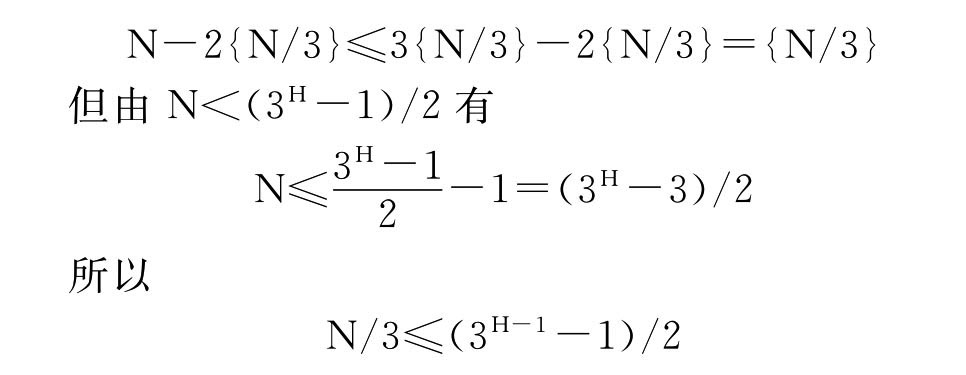
右边一定是一个整数，所以我们最终得到

N-2｛N／3｝≤｛N／3｝≤（3^H-1-1）／2。

根据归纳假设，在有标准球的情况下，N-2｛N／3｝个球的问题可被H-1次的称量解决。

如果左边重，则要么是坏球比较轻，而且坏球在右面｛N／3｝个球里；要么是坏球比较重，而且坏球在左面｛N／3｝个球里。这时根据结论1，我们还要｛log₃（2｛N／3｝）｝次来找到坏球并知其轻重。和上面的计算完全一样，

所以仍旧可以用剩下的H-1次称量解决问题。

如果右边重，完全类似于左边重的情况。

现在考虑N＝（3^H-1）／2的情况，这时允许用一个标准球。

我们可以把球分成三堆。第一堆为（3^H-1＋1）／2个，第二堆为（3^H-1＋1）／2个再加上标准球，所以第二堆一共也是（3^H-1＋1）／2个球，第三堆剩下：

（3^H-1）／2-（3^H-1＋1）／2-（3^H-1＋1）／2＝（3^H-1＋1）／2个球

我们把第一和第二堆小球放在天平左右端进行第一次称量。

三种情况：

如果天平平衡，那么坏球在第三堆的（3^H-1＋1）／2个里。根据归纳假设，在有标准球的情况下，这可被H-1次称量解决。

如果左边重，则要么是坏球比较轻，而且坏球在右面（3^H-1＋1）／2个球里；要么是坏球比较重，而且坏球在左面除了附加的标准球以外的（3^H-1＋1）／2个球里。这时根据结论1，我们还要进行

｛log₃（3^H-1＋1）／2＋（3^H-1＋1）／2）｝＝H-1次

来找到坏球并知其轻重。

所以这也可以用剩下的H-1次称量来解决问题。

如果右边重，完全类似于左边重的情况。

这就完全证明了结论2中的2）、4）和5）。剩下的就是3）的前半部分：

如果N＝（3^H-1）／2，那么称H次足以保证找到坏球（但可能不知道轻重）。

这很简单，如果我们拿掉一个球，那么根据2），一定能用H次称量来找到坏球并且知道轻重——唯一的例外是，如果被拿掉的那个恰好就是坏球——那么这时候所有称量的结果都是天平保持平衡。

如果发生了这样的事，所有称量的结果都是天平保持平衡，我们就可以断定坏球就是那个被拿掉的球，当然这时这个球从来没有上过天平，我们绝无可能知道它是比标准球重，还是比标准球轻。