矢量绕定轴转动公式

5.7.3　矢量绕定轴转动公式

1）矢量绕定轴转动公式

在平面镜或反射棱镜的实际应用中，经常遇到如下两种类型问题：

（1）有些光学仪器为了扩大观察测量范围，需要进行方向和高低扫描，使仪器的光轴方向能连续改变。为此，常利用某一平面反射元件绕某固定轴线转动ω角。这样，平面镜的法线矢量N或角镜的棱线矢量P的空间位置将要改变。因此，为解决变化后的特征矢量N、P的确定问题，需研究空间矢量绕定轴转动问题；

（2）由于棱镜或平面镜系的角度制造误差及装配位置误差，使反射面法线或角镜棱线相对于设计的正确位置发生微量偏转Δω角，这将引起光轴偏差及像面偏转（倾斜）。为此，也需要研究矢量绕定轴转动问题。

上述两方面均需解决的一个共同问题是：空间一矢量A（例如平面镜或反射棱镜的法线矢量或棱线矢量）绕空间某一轴线P转动ω角，所得到的新矢量A＇应如何计算?

如图5.45所示，初始的单位矢量A与转轴单位矢量P已知，其夹角为φ，A在与P垂直的平面M上的投影为矢量B（非单位矢量）。若A绕P按右手螺旋定则转过ω角，得到新矢量A＇（为单位矢量）。显然，A＇与P的夹角亦为φ。下面导出A＇与A、P、ω的函数关系式。由图示应有

A=B+（A·P）P=B+cosφP　　　　　　　　　　　　　　（5.64a）

图5.45　矢量绕定轴转动

设A＇在M平面上的投影为B＇（亦非单位矢量），B＇在B上的投影为D，则应有

A＇=B＇+（A＇·P）P=（D+C）+cosφP　　　　　　　　（5.64b）

其中

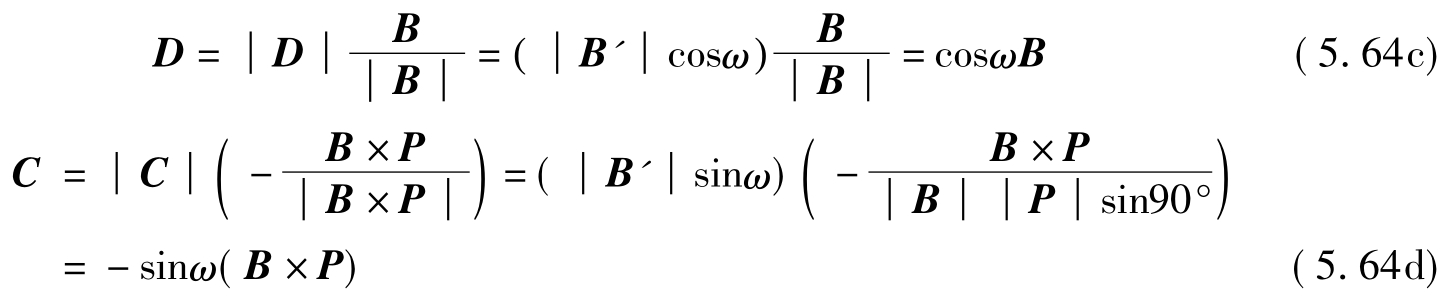
将式（c）、式（d）代入式（b）并经整理最终得到

A＇=cosωA+（1－cosω）（A·P）P－sinω（A×P）　　　　　　（5.65）

上式就是重要的矢量绕定轴转动公式，若知道A、P和转角ω，则旋转后的矢量A＇即可求出，式中的转角ω可为任意值。

特别情况，在微量转动情况下，Δω很小，可以略去其二阶以上小量，因而有sinΔω=Δω，cosΔω=1，因而式（5.65）可以简化为

A＇=A－Δω（A×P）　　　　　　　　　　　　　　（5.66）

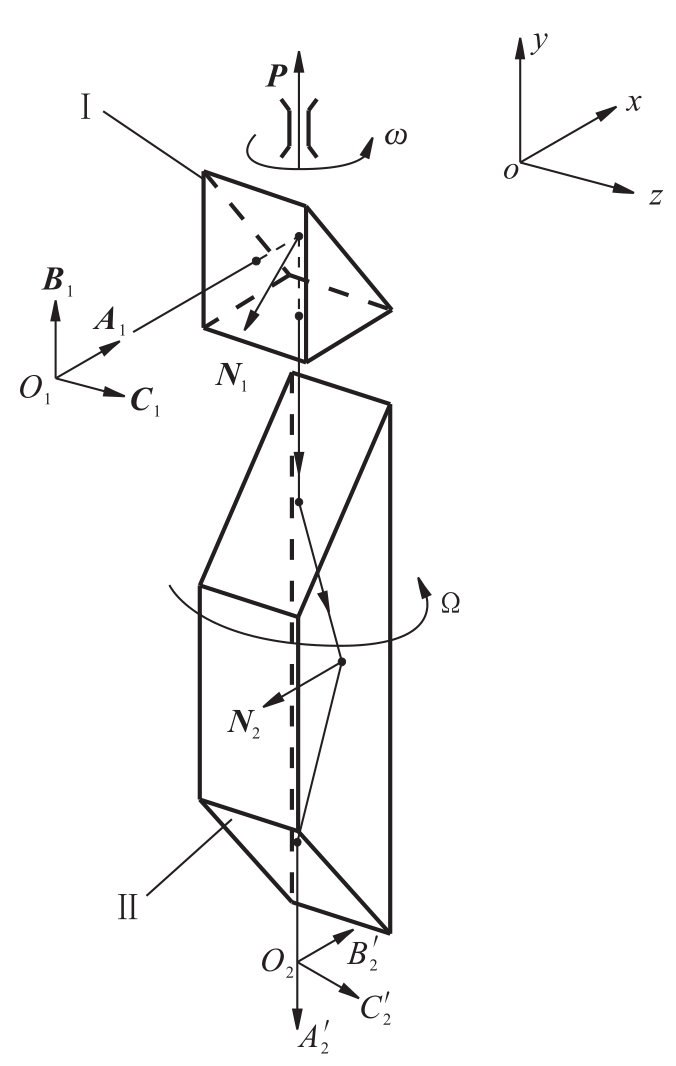
图5.46　周视棱镜系统的矢量分析计算

这就是矢量绕定轴微量转动公式，它有重要的实用意义。可用来计算平面镜系的特征矢量（法线或棱线矢量）由于装配位置或角度制造误差而引起的绕定轴微量偏转所形成的新矢量；进而计算由于特征矢量微量转动而引起的光轴偏差与像面偏转（倾斜）。

这里的“光轴偏差”是指系统中由于平面镜系的位置误差及棱镜角度误差引起的出射光轴相对于设计要求的出射光轴方向的偏差。计算时通常取沿光轴的单位矢量作为入射光轴矢量，计算其出射光轴；“像倾斜”是指像面绕出射光轴相对于像面正确方位的偏转。计算像倾斜时，通常取垂直于入射光轴的单位矢量作为物矢量，计算其像矢量。

下面结合典型周视棱镜系统，说明式（5.57）～式（5.65）等公式的应用与分析计算方法。

［例5.2］　计算分析当直角棱镜Ⅰ周视绕P轴旋转ω角时，为补偿由于棱镜Ⅰ旋转引起的像面偏转，道威棱镜Ⅱ绕P轴的旋转角度Ω应为多大（见图5.46）?

［解］　首先建立固定的右手直角坐标系o－xyz作为基准。

（1）初始状态：直角棱镜Ⅰ和道威棱镜Ⅱ均未转动，其光轴截面同在xoy平面内。取初始物坐标o₁－A₁B₁C₁与o－xyz一致，各反射面法线与物像坐标矢量分别为

法线矢量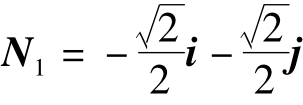：；N₂=－i；

光轴矢量：A₁=i；A₁＇=－j；A₂＇=－j；

物面与像面矢量：B₁=j；B₁＇=－i；B₂＇=i；

　　　　　　　　C₁=k；C₁＇=k；C₂＇=k；

（2）周视转动：以初始状态为标准，如果棱镜Ⅰ绕y轴周视转动时，棱镜Ⅱ与棱镜Ⅰ的转动相配合，能得到与初始状态相同的像坐标（即A₂＇=－j，B₂＇=i，C₂＇=k），则两者转动对像面偏转的影响互相补偿。设转轴矢量P=j，棱镜Ⅰ绕P轴转动ω角，而棱镜Ⅱ绕P轴转动Ω角可与之相补偿，则转动后各法线矢量和物像坐标矢量应有如下结果：

①棱镜Ⅰ绕P轴转动ω后，其法线矢量为

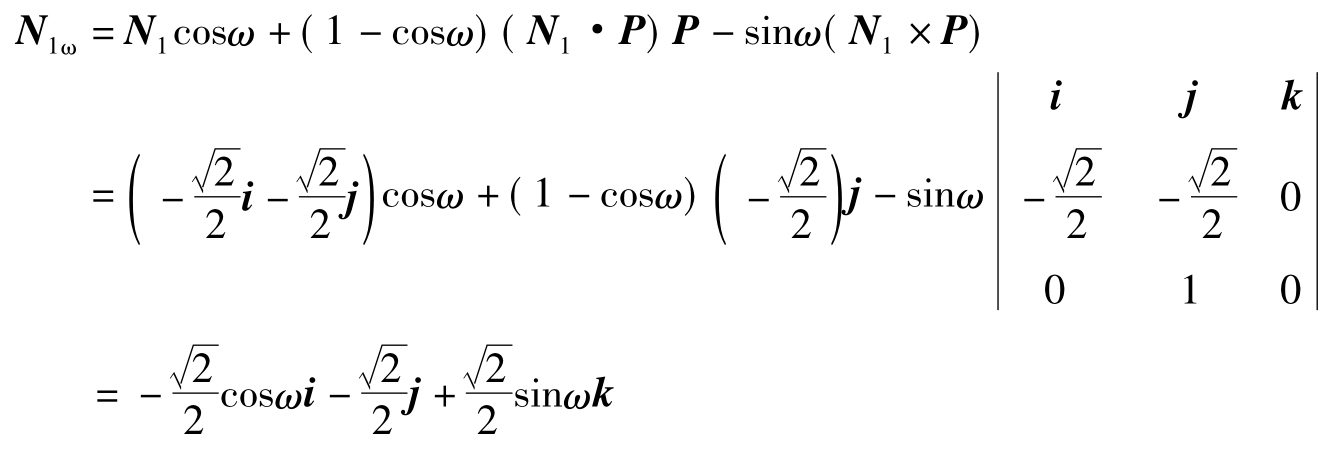
棱镜Ⅰ转动后所对准的新物坐标应为（相对于固定坐标系）

A_1ω=cosωi－sinωk；　B_1ω=j；　C_1ω=sinωi+cosωk

新物坐标经转动的棱镜Ⅰ反射，得到：

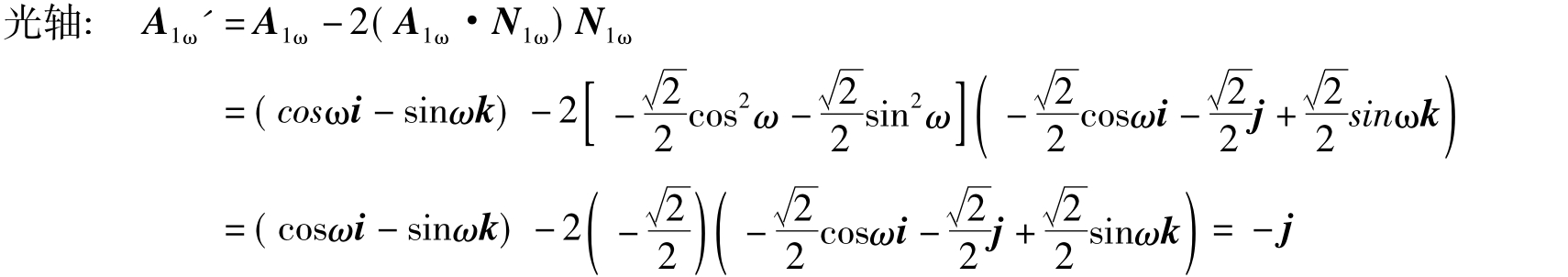
像面：

上述结果表明，光轴未变化，像面发生偏转。

②道威棱镜Ⅱ绕P轴转Ω角。转动后的法线矢量：

N_2Ω=N₂cosΩ+（1－cosΩ）（N₂·P）P－sinΩ（N₂×P）=－cosΩi+sinΩk

棱镜Ⅱ的物坐标应有：A_2Ω=A_1ω＇；B_2Ω=B_1ω＇；C_2Ω=C_1ω＇

A_2Ω、B_2Ω、C_2Ω经转动Ω角的棱镜Ⅱ反射后，其像坐标为

光轴：A_2Ω＇=A_2Ω－2（A_2Ω·N_2Ω）N_2Ω

　　　　　　=－j－2［（－j）（－cosΩi+sinΩk）］（－cosΩi+sinΩk）=－j

像面：

将上述结果与初始状态像坐标A₂＇、B₂＇、C₂＇比较发现：

（1）A＇_2Ω=A₂＇=－j，即当棱镜Ⅰ和Ⅱ分别绕P转动ω和Ω角时，光轴始终不变；

（2）若要求棱镜Ⅰ周视时，像面不发生偏转，即B_2Ω＇=B₂＇=i，C_2Ω＇=C₂＇=k。则要求ω－2Ω=0，即。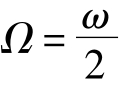

由此可得到结论：当道威棱镜Ⅱ与直角棱镜Ⅰ以速比1∶2的关系绕P轴同向转动时，则由棱镜Ⅰ周视所引起的像面偏转将得到补偿。

用类似的方法利用式（5.66），可以计算分析出由于棱镜加工的角度误差和安装位置误差所导致的特征矢量（N、P等）微量偏转Δω角所引起的光轴偏差与像倾斜（像面偏转），而且由于式（5.66）为微量转角近似计算公式，因而计算大为简化。

2）空间光线经二面角镜的反射——矢量绕定轴转动公式在二面角镜中的应用

空间光线经二面角镜的反射成像可以视为矢量绕定轴转动公式在二面角镜中的具体应用。

如图5.47所示，A、A＇、A″分别表示入射光线和两反射光线的方向，一般情况下，三者不共面；N₁、N₂分别表示反射面Ⅰ和Ⅱ的法线，α为两反射面的夹角。

图5.47　空间光线经二面角镜的反射

对两反射面分别应用第一反射定律式（5.56）：

A×N₁=A＇×N₁　　　　　　　　　　　　（5.67a）

A＇×N₂=A″×N₂　　　　　　　　　　　　（5.67b）

以N₂、N₁分别对式（a）和式（b）作标积：

N₂·（A×N₁）=N₂·（A＇×N₁）　　　　　（5.67c）

N₁·（A＇×N₂）=N₁·（A″×N₂）　　　　（5.67d）

利用三个矢量混合积性质的一般表达式：

A·（B×C）=B·（C×A）=C·（A×B）

则式（c）可以写为

A·（N₁×N₂）=A＇·（N₁×N₂）

由于N₁×N₂=－N₂×N₁，因而上式可进一步改写为：

A·（N₂×N₁）=A＇·（N₂×N₁）　　　　（5.67e）

相应地，式（d）可以写为

A＇·（N₂×N₁）=A″·（N₂×N₁）　　　　（5.67f）

比较式（e）、式（f）两式，得到

A·（N₂×N₁）=A＇·（N₂×N₁）=A″·（N₂×N₁）　　　　（5.68）

上式中，N₂×N₁为一新矢量，其方向按右手螺旋法则指向垂直于由N₂和N₁所决定的平面的方向，即二面角镜的棱线方向；其大小为

│N₂×N₁│=│N₂││N₁│sin（180°－α）=sinα

若定义P为二面角镜棱线方向的单位矢量，则有

N₂×N₁=Psinα　　　　　　　　　　（5.69）

将上式代入式（5.68）并约去sinα，则有

A·P=A＇·P=A″·P　　　　　　　　　　　　　（5.70）

由于A、A＇、A″、P均为单位矢量，因而上式表明A、A＇、A″三者与P的夹角都相等。由此可推论：经二面角镜反射后的出射光线矢量A″，可视为由入射光线矢量A绕棱线矢量P旋转某一角度ω得到（可将A、A″的起始点移至角镜棱P上的同一点）。这表明二面角镜的出射光线矢量A″可按式（5.68）计算得到。

广义地说，二面角镜的像空间可由其物空间绕角镜的棱线矢量P旋转ω角得到。旋转的角度ω应为何值?由于转角ω恰是A与A″在垂直于棱镜矢量P的平面上的投影间的夹角；而5.4节中式（5.34）业已证明：在垂直于角镜棱线的主截面内，出射光线与入射光线的夹角为角镜二面角ω的二倍。因此得到：ω=2α。将此结果代入式（5.65），则有：

A″=Acos2α+（1－cos2α）（A·P）P－sin2α（A×P）　　　　　　　（5.71）

上式即为二面角镜的反射公式，因而只要知道A、P和α即可求出A″；且如果A不变，角镜绕棱线P任意转动（即P不变），则A″均不变。

对经常有重要应用的如下几种特殊情况，上式演变为

α=45°，A″=（A·P）P－A×P　　　　　　　　　　（5.72）

α=90°，A″=－A+2（A·P）P　　　　　　　　　　　（5.73）