学习混合高斯分布

时间：2022-02-11 理论教育版权反馈

【摘要】：聚类方法假定数据是由一个混合分布P生成的。令随机变量C代表成份，取值为1, ... , k，则混合分布由下式给出：其中x代表一个数据点的属性值。在连续型数据的情况下，对于成份的分布的一个自然选择就是多元高斯分布，也就是所谓的混合高斯分布族。混合高斯分布的参数是wi= P， μi，以及i。图20.8所示的是3个高斯分布的混合，这个分布实际上是图中的数据来源。有3种成份的混合高斯分布模型，权值为0.2，0.3和0.5。

20.3.1 无监督聚类：学习混合高斯分布

无监督聚类是一个在对象集上辨识多种类别的问题。这个问题是无监督的，因为没有给出类别的标记。例如，设想我们记录了 10 万颗恒星的光谱，通过光谱能揭示出恒星的不同类型吗？如果可以，它们有多少特性，以及特性有哪些？我们都听说过诸如“红巨星”和“白矮星”这样的术语，但是恒星不会把这些标签写在自己的帽子上——天文学家们必须执行无监督的聚类来辨识它们的类别。其它例子还包括在林奈（Linnæan）生物分类学中对种、属、目等等的辨识，以及创建自然种类对普通物体划分类别（参见第十章）。

无监督聚类从数据入手。图20.8（a）中显示了500个数据点，每个点指定两个连续属性的值。这些数据点与恒星相对应，而属性可以与在两个特定频率上的光谱强度相对应。下一步，我们需要理解何种可能的分布会产生这些数据。聚类方法假定数据是由一个混合分布P生成的。这样的分布有k种成份，每种成份自身是一个分布。数据点的生成是通过先选择一种成份、然后根据该成份生成一个实例而完成的。令随机变量C代表成份，取值为1, ... , k，则混合分布由下式给出：

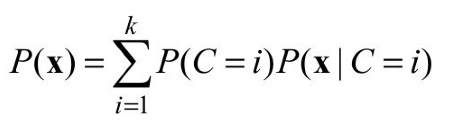
其中x代表一个数据点的属性值。在连续型数据的情况下，对于成份的分布的一个自然选择就是多元高斯分布，也就是所谓的混合高斯分布族。混合高斯分布的参数是wi= P(C = i)（即每种成份的权值）， μi（每种成份的均值），以及i（每种成份的协方差）。图20.8（b）所示的是3个高斯分布的混合，这个分布实际上是图（a）中的数据来源。

图20.8 （a）在二维平面上的500个数据点，构成3个簇。（b）有3种成份的混合高斯分布模型，权值（从左到右）为0.2，0.3和0.5。（a）中的数据是根据这个模型生成的。（c）根据（b）中数据通过EM对模型进行的重构

于是，无监督聚类问题就是要从类似于图20.8（a）中的原始数据恢复出一个类似于图20.8（b）中所示的混合模型。很明显，如果我们知道哪种成份产生了每个数据点，那么就更容易恢复出每种成份的高斯分布：我们可以从给定的成份中选出所有的数据点，然后用公式（20.4）（的一个多元版本）来拟合数据集的高斯分布的参数。另一方面，如果我们知道每种成份的参数，那么我们至少可以在一定的概率意义下将每个数据点分配到某种成份。问题在于我们既不知道分配也不知道参数。

在这种背景下EM方法的基本思想是，假装我们知道模型的参数，然后推断出每个数据点属于每种成份的概率。接下来，我们用成份对数据进行重新拟合，每种成份都针对整个数据集进行拟合，根据每个数据点属于每种成份的概率对其加权。这个过程迭代进行，直到收敛为止。本质上，我们是基于当前的模型，通过推断隐变量的概率分布——每个数据点属于哪种成份——的方式对数据进行“完备化”。对于混合高斯模型，我们可以任意初始化混合模型的参数，然后按照下面的两步过程进行迭代：

（1）E步骤：计算概率pi j= P(C = i|xj)，数据xj由成份i生成的概率。根据贝叶斯法则，我们得到pi j= α P( xj|C = i ) P(C = i )。P( xj|C = i )项就是第i个高斯分布中xj的概率，而P(C = i )项就是第i个高斯分布的加权参数。这里定义pi=Σjpi j。

（2）M步骤：计算新的均值、协方差和成份权重如下：

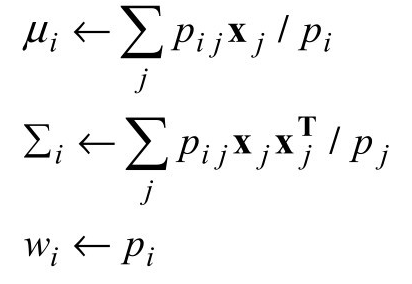
E步骤，或称为期望步骤，可以被视为计算隐含的指示变量Zij的期望值pij，其中如果数据xj是由第i个成份生成的，则Zi j取1，否则取0。M步骤，或称为最大化步骤，在给定隐含指示变量的期望值的条件下，寻找使数据的对数似然最大化的新参数值。

当EM学习用于图20.8（a）中数据时，其最后一个模型如图20.8（c）所示；它在视觉上很难和生成数据的原始模型区分开。图 20.9（a）在 EM 进展中根据当前模型绘制了数据的对数似然。这里有两点需要注意。第一，最后学习到的模型的对数似然稍微超过了生成数据的原始模型。这看起来可能有些奇怪，不过它恰好反映了数据是随机生成的，因而可能无法准确反映底层模型这一事实。第二点是，EM 在每次迭代中增加了数据的对数似然。这个事实很容易被总体上证明。此外，在一定条件下，可以证明EM能够达到似然的局部极大值。（在很少的情况下，它可以到达一个鞍点或者甚至一个局部极小值。）在这种意义上，EM类似于一个基于梯度的爬山法算法，但是要注意它没有“步长”这个参数！

实际情况并不总是像图20.9（a）中那样好的。有时候，会发生例如一个高斯成份缩小的情况，以至于只覆盖了一个单个的数据点。那么它的方差会等于 0，而似然概率成为无穷大！另一个问题是，两个成份可能发生“合并”，得到相同的均值和方差，并共享它们的数据点。这类退化的局部极大的情况是很严重的问题，尤其在高维度的时候。一种解决方案是在模型参数上设置先验，并且应用 MAP版本的EM算法。另一种方案是，如果一种成份太小或者太接近于另一种成份，就使用新的随机参数重新开始一种成份。这还有助于使用合理的值来对参数进行初始化。