参数式函数的导数

在xOy-平面上表示平面曲线C的最自由的方式是：分别由两个单变量的函数φ（t）和φ（t）表示变量x和y，

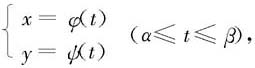
即C＝｛（x,y）｜x＝φ（t）,y＝φ（t）,t∈（α,β）｝．如果φ（t）和φ（t）都有连续的导函数，并且对任何t∈［α,β］，φ′（t）和φ′（t）不同时为零，则我们称此平面曲线是光滑的。

光滑性要求可以确保参数曲线C上的任何一点（x₀，y₀）＝（φ（t₀），φ（t₀））处均有切线。事实上，如果参数曲线C是光滑的，则（φ′（t₀），φ′（t₀））≠（0,0）．不妨设φ′（t₀）≠0．则由φ（t）的连续性，在t₀的某个邻域N（t₀）（如果t₀为区间端点，则为单侧邻域）内φ′（t）非零且保号，从而φ（t）严格单调，并且在x₀＝φ（t₀）的某个小邻域N（x₀）内有反函数t＝φ^-1（x）．因此在N（x₀）内，y＝φ（φ^-1（x））．显然，由y＝φ（φ^-1（x））确定的曲线

｛（x,y）｜y＝φ（φ^-1（x））,x∈N（x₀）｝

与C上的在（x₀，y₀）附近的局部曲线C₀＝｛（x,y）｜x＝φ（t）,y＝φ（t）,t∈N（t₀）｝是相同的。根据定理3.6，此函数在x₀处可导，

因而在（x₀，y₀）处有切线。

一般地，如果在［α,β］内φ′连续且非零，则有反函数φ^-1∶［a,b］→［α,β］，其中

a＝min（φ（α）,φ（β）），b＝max（φ（α）,φ（β））．

从而由y＝φ（φ^-1（x）），x∈［a,b］确定的曲线即为C．在这个意义下，我们称曲线C的参数函数表示式

为函数φ°φ^-1的参数式，简称参数式函数。

当我们论述“参数式函数的导数”时，意为y＝φ（φ^-1（x））的导函数

此时，导函数仍然可以表示为一个参数式函数：

例3.4.1　考虑参数表示下的摆线

（关于x）的导函数