函数方向导数定义

对函数的全局性把握，是建立在对函数局部性的理解之上的。函数的“点点”连续性是一个重要的局部性质。本节将讨论建立在局部变化率基础之上的函数局部性：函数的导数与微分。

考虑函数f在点x₀附近的局部变化率（这里我们假定f在x₀的某个邻域内有定义）：

这个变化率在应用中有其实际意义。例如，如果f（t）表示时间t内某个物体运动的路程（这里自变量用t表示，以便与习惯一致，相应地x₀改用为t₀），则相应的变化率k（t）表示该物体在时间段［t₀，t］内的平均速度。又如，对某个非均匀质量分布的竿状物，如果f（x）表示为离指定端点距离为x的这一段的质量，则变化率k（x）为x₀到x这一段的平均线密度。对一般的函数，从数学上说，局部变化率k（x）在几何上表示平面上过两点（x₀，f（x₀））和（x，f（x））的直线（称为过定点（x₀，f（x₀））的割线）的斜率。

图3.1　曲线的割线

一般地，局部变化率k（x）仍然具有（相对小的）局部整体性。显然，当x充分接近（但又不同）于x₀时，这种整体性的范围逐渐缩小为一点。因此，合理地，我们可以用极限值

（如果存在的话）定义为f在点x₀处的变化率。与此同时，x趋于x₀时，过定点（x₀，f（x₀））的动态割线也趋于稳定。这一稳定的直线，称为曲线C∶y＝f（x）在点（x₀，f（x₀））处的切线，简称为f在x₀处的切线。显然，此切线的斜率为k₀且切线与x轴不垂直。

下面我们从另一方面考虑一个具有几何意义的局部性问题：曲线y＝f（x）在（x₀，f（x₀））附近是否能够“近似地”视为（与x轴不垂直的）直线？我们从正反两方面来考虑。

首先假设这样的直线y＝l（x）存在。显然它应该过点（x₀，f（x₀）），即l（x₀）＝f（x₀）．因此可设l（x）＝f（x₀）＋k（x－x₀），其中k为待定的直线斜率。其次，上述“近似”性度量应该是一个x－x₀的高阶小量，即f（x）－l（x）＝o（x－x₀），（x→x₀）．将l（x）＝f（x₀）＋k（x－x₀）代入，并令x→x₀，则有

反过来，考虑f在x₀处的切线l（x）＝f（x₀）＋k₀（x－x₀）作为这样的候选直线。由k₀的定义，容易验证f（x）－l（x）＝o（x－x₀），（x→x₀）．这说明f在x₀处的切线正是这样的直线：曲线y＝f（x）在（x₀，f（x₀））附近确实能够近似地视为直线y＝l（x），近似度为o（x－x₀）．

上述分析的基础是极限（1）存在。这正是如下导数的定义。

定义3.1.1　设函数f在x₀的某个邻域内有定义。如果极限

存在，则称f在x₀处可导，x₀为f的可导点，k为f在x₀处的导数值，并将导数值改记为f′（x₀）；当此极限不存在时，则称f在x₀处不可导。

导数值还有其他记号：

根据定义，函数f在x₀可导，其首要条件是f在x₀的某个邻域内有定义。因此，当我们论述“f在x₀可导”时，我们隐含地假定f在x₀的某个邻域内有定义，而不关心这个邻域的大小。必要时，我们仍将明确函数的定义域。

显而易见，任何常值函数在任何点都可导，且导数为零。对于一些简单的函数，可以直接根据定义来判断可导性或计算导数值。下面是一个简单的例子。

例3.1.2　考虑f（x）＝x²在x₀＝0和x₀＝3处的可导性。

解　通过简单计算，可得

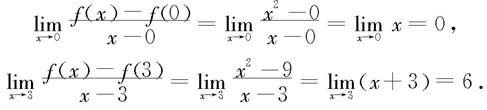
因此f在x₀＝0和x₀＝3处都可导，且f′（0）＝0，f′（3）＝6．

实际上，f（x）＝x²在任何一点x₀处都可导，且

导函数

如果函数在区间（a,b）内的任何一点处均可导，则由x∈（a,b）到导数值f′（x）的对应关系确定一个新的函数我们称其为f在区间（a,b）内的导函数。

导函数也简称为导数。根据定义，对x∈（a,b），

后一种表示显得简单。请注意：在上述极限过程中，x始终是一个固定的量，尽管在取极限之前或之后，它可以在所在的区间内任意取定。

导函数可有许多不同的表示符号。我们知道可以用不同符号表示同一函数的自变量。当我们明确f的自变量用x表示时，则f的导函数f′也可记为习惯上，常用记号y表示函数f的应变量：y＝f（x）．此时也用y′表示f的导函数。特别地，也用（f（x））′表示关于函数f中的指定变量x求导。因此有如下明确关系：f′（x）＝（f（x））′．

需要注意的是：导数符号是一个整体记号。目前我们暂时不能将其看作是一个商。当引入微分的概念后，我们方能够将其看作是两个微分的商。那时，我们又称导数是微商——微分之商。

例3.1.3　求f（x）＝x^α的导数（α≠0）．

解　根据定义，当x≠0时，

这里我们用到了结论（见例题2.3.6（4）．）　　◇

例3.1.4　求y＝sinx和y＝cosx的导函数。

解　由三角函数的和差化积公式，因此，

即（sinx）′＝cosx．类似地有

例3.1.5　求y＝lnx的导函数（x＞0）．

解　因为

所以

如果f是一个分段表示的函数，x₀为定义区间的一个分段点，如

则应特别注意f的定义区间分段点x₀的可导性。通常，f在x₀处是否有导数值，应通过定义确定。

例3.1.6　考虑函数

的可导性。

解　对每个固定的x，如果x＜0，则当｜∆x｜充分小时，也有x＋∆x＜0，于是，

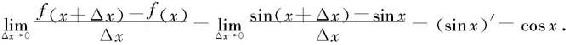
因此，当x＜0时，f′（x）＝cosx．同理，如果x＞0，则f′（x）＝（cx）′＝c．但是，如果x＝0，则由定义，

只有当c＝1时，f在x＝0处才可导：即

复杂函数的求导计算，将建立在下一节给出的导数运算法则的基础之上。

可导函数的连续性

根据定义，f在x₀处可导意味着f（x）－f（x₀）＝o（x－x₀），这说明

即f在x₀处连续。这就是下述定理。

定理3.1.7　设f在x₀的某个邻域内有定义，则f在x₀处可导的必要条件是：f在x₀处连续。

不可导的函数

上述定理表明，并非任何函数在所指定点x₀处都可导：如果f在x₀处不连续，则f在x₀处不可导，然而，即使f在某点处连续，f在此点处仍然有可能不可导，下面是一个简单例子。

例3.1.8　函数f（x）＝｜x｜在x＝0处不可导，这是因为极限不存在。

从几何上来看，x＝0所对应的原点（0,0）是曲线y＝｜x｜的一个“尖点”。考查过“尖点”的动态割线。显然，当动点交替地位于“尖点”的两侧趋于该定点时，动态割线在两条固定的直线y＝x和y＝－x摆动，没有“稳定状态”。

函数的不可导性远比上面两种具有几何直观的情形（间断点或“尖点”）要复杂得多。图3.2给出了3个在x＝0处连续但不可导的函数曲线。

图3.2　在x＝0处连续但不可导的函数

单侧导数

考虑函数f在x₀的可导性时，首先要求f在x₀的某个邻域内有定义。如果f仅在x₀的某一侧有定义（如x₀为区间端点），则定义3.1.1不适用。另一方面，类似于例题3.1.8所示的函数，在x₀的每个单侧都分别具有很好的性质。为研究这样一类函数的性质，我们退而考虑函数的单侧可导性。

定义3.1.9　设函数f在x₀的某个含x₀的右邻域［x₀，x₀＋δ］内有定义。如果右极限

存在，则称f在x₀处右侧可导，k为f在x₀处的右导数（值），并记其为f′＋（x₀）．类似地定义f在x₀处的左导数f′－（x₀）．

显然，函数f（x）＝｜x｜在x＝0处的左、右导数者存在，且f′－（0）＝－1，f′＋（0）＝1．

对于图3.2中间所示的函数在x＝0处的左导数不存在：

但右导数存在：

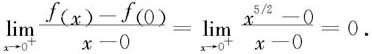
读者可以验证：图3.2右侧所示的函数在x＝0处的左、右导数都不存在。

导数与左、右导数之间的下述关系是显而易见的，读者可试着加以证明。

定理3.1.10．　设函数f在x₀的某个邻域内有定义。则f在x₀处可导，当且仅当f在x₀处分别左、右可导，且左、右导数值相等。进一步地，在可导的前提下，

f′－（x₀）＝f′（x₀）＝f′＋（x₀）．