相对论和微粒

我现在要证明，根据广义相对论，场方程有不带奇点的解，这种解能解释成为表示微粒的。这里我只限于中性粒子，因为新近发表的同罗森博士合作的另一篇论文中，我已详尽地处理了这个问题，同时因为在这种情况下，问题的实质能完全显示出来。

引力场是完全用张量g_μν来描述的。在三指标符号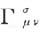中也出现了抗变的g^μν，它的定义是g_μν的子式除以行列式g（＝∣g_αβ∣）．要使R_ik成为确定的并且是非无限小的，就必须要求在连续区每一点的邻近都有这样一个坐标系，用这个坐标系来表示，g_μν及其第一阶微分系数都是连续的并且是可微分的，这还不够，还必须使行列式g无论在哪里都不能等于零。可是，如果人们把微分方程R_ik＝0用g²R_ik＝0来代替，那么上述最后一个限制就不存在了，因为这个方程的左边是g_ik及其导数的有理整函数。

这些方程有由施瓦兹·希耳德得出的中心对称解

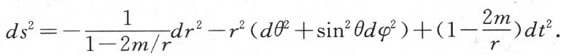
这个解在r＝2m处有一奇点，因为dr²的系数（即g₁₁）在这个超曲面上变成无限。可是，如果我们把变数r用下列方程定义的ρ来代替：

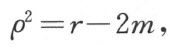
我们就得到

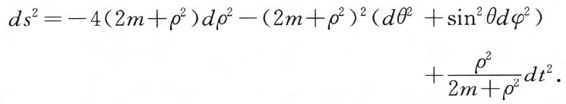
这个解对于ρ的一切数值都是正则的。对于ρ＝0，dt²的系数（即g₄₄）也等于零，这件事固然得出了对于这个数值的行列式g等于零的结果；但用这些实际采用的场方程的写法，它并不构成奇点。

如果ρ从－∞变到＋∞，那么r就从＋∞变到r＝2m，然后又回到＋∞；但对于r<2m的那些r值，并没有对应的ρ的实数值。因此，通过把物理空间表示为由两片沿着超曲面ρ＝0（也就是r＝2m）相接触的同样的“叶”所组成，而在这个超曲面上，行列式g等于零，施瓦兹·希耳德解就变成一个正则解。让我们把两片（同样的）“叶”之间的这种连接叫做“桥”。因此，有限区域里两片“叶”之间的这种桥的存在，就相当于物质的中性粒子的存在，而这种粒子可用一种不带奇点的方式来描述。

解决几个中性粒子的运动问题，显然就等于去发现引力方程（写成不带分母的形式）的那些含有几个“桥”的解。

由于“桥”在本性上是一种分立的元素，因此，上述概念就先验地对应于物质的原子论性的结构。而且，我们看出中性粒子的质量常数m必然是正的，因为没有一个不带奇点的解能同一个m是负值的施瓦兹·希耳德解相对应。只有考查多桥问题，才能证明这种理论方法是否能解释经验上显示出来的自然界中所找到的那些粒子质量的等同性，以及它是否能说明那些已为量子力学那么奇妙地理解到的事实。

以类似的方式，也可能说明引力方程同电方程的结合（在引力方程中适当选取电的部分的正负号）产生电微粒的不带奇点的桥表示。这种解中最简单的是关于无引力质量的电粒子的解。

只要解决多桥问题所碰到的巨大的数学困难还没有克服，从物理学家的观点来看，就无法讲到这理论的实效。可是事实上，它却是把一种可能解释物质性质的场论不断加以提炼的第一个尝试。为了支持这种尝试，人们还应当再加上一个理由：它所根据的，是今天已知的可能最简单的相对论性场方程。