婚姻和一般联合体的平均持续时间

构造死亡表的方法非常简单。可以从民事登记册上获取出生和死亡的人数。可以了解到有多少人在出生后第一年死去，多少人在第二年夭折，等等。从这些数字中，可以推出在每年之始活着的人数有多少，可以把这个数字记录在表中表示年龄的那一栏中。依此，把出生数记录在零岁的旁边，把达到一岁的婴儿数记录在1岁的旁边，把达到两岁的孩子记录写在2岁的旁边，其余的以此类推。但是，因为在生命的前两年死亡率非常高，为了更精确一些，在人生的第一年，在每半年末就必须注明生存者的数目。

如果我们将记录在死亡表上的所有个体的生命之和被这些个体的人数所除，就会得到对应于这个表的生命的平均持续时间。为了做到这一点，将半岁乘以第一年死亡的人数——这个数字等于写在零岁与1岁旁边的人数之差。他们的死亡率必须分布在一整年中，而其生命的平均持续时间只为半年。那么，将1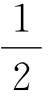岁乘以第二年死亡的人数，2岁乘以第三年死亡的人数，以此类推。这些积之和被出生数所除就会给出生命的平均持续时间。从这里很容易得出结论：通过以下方法就会得到这个平均持续时间：求出在这个表格中每一岁旁边的数字之和，用出生数除之，这个商再减去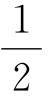岁作为单位。那么从任何年龄开始，剩下的生命平均持续时间可以用同样的方式求出，从达到这个年龄的所有人数开始，就像对出生人数所作的那样。但是，并非从出生时刻算起，生命的平均持续时间就是最大的，正是此时婴儿期的危险被忽略了，这时的生命的平均持续时间为四十三岁。从一个给定的年龄起，活到某一年龄的概率等于表格中在这两个年龄旁记录的人数之比。

这些数字的精确性需求非常庞大的出生数字用于表的制作。分析会给出一些非常简单的公式用以估计这些表中所记录的数字将在相距很近的极限之间偏离真值的概率。从这些公式中我们将会看到，随着所考察的出生数的增加，这些极限之间的间隔会减小，这个概率会增大。所以，如果所应用的出生人数变为无穷大时，死亡表将会精确地呈现出死亡率的真正法则。

所以，死亡表就是人类寿命的概率的一种表格。记录在每一年龄旁边的人数与出生数之比将是一个新生儿活到这个年龄的概率。以同样的方式，可以估计一个期望的值，将每一期望的获利与得到它的概率相乘，再将这些积相加，那么我们即可类似地估计出生命平均持续时间：将每一年龄与达到其开始和终结的概率之和的一半相乘，将这些积相加，由此可以导出上述发现的结果。但是，这种思考生命平均持续时间的方式在稳定的人口状态下具有一定的优势，即在出生数与死亡数相同的情况下，生命平均持续时间人口数量与年出生人口的数量之比，因为，如果假设人口是稳定的，表中两个相继年龄之间的某一年龄的人数乘以达到这些年龄的概率之和的一半，那么所有的这些乘积之和就是全部的人口数。现在，容易看到，这个和被年出生数所除，与我们刚刚已经定义的生命平均持续时间是一致的。

借助于死亡表，很容易构造相应的假设为稳定的人口表。为此，我们求出死亡表中对应于年龄零岁，一岁，两岁，三岁等人数的算术平均数。所有这些平均数之和就是全部人口。把它写在零岁近旁。如果从这个和减去第一个平均数，余数就是一岁或更大年龄的人数，把它写在一岁的近旁，从这个余数中减去第二个平均值，第二个余数是两岁或者年龄更大的人数，把这个数写在二岁近旁，以此类推。

死亡率受到如此之多的可变原因的影响，以至于表示它的表格应该因时间和地点的不同而发生变化。在这方面各种各样的生命状态展现了关于与每种生命状态密切相连的灾难与风险的明确差别，必须以建立在寿命基础上的计算来考虑它们。但是，这些差别还没有得以被充分地认识。将来总有一天它们会被充分地认识，那时我们就会知道每一行业需要付出怎样的生命代价，我们将受惠于使这些风险降低的知识。

土地的状况、海拔高度、气温、居民的习惯，以及政府的运作都对死亡率有着相当大的影响。但是，在对观察到的差别的原因进行考查之前，通常需要对显示出这个原因的概率进行研究。由此，在法国，我们已经看到人口与年出生数之比上升到了28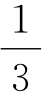，这不同于古代米兰（Milan）公国的二十五，这两个比都建立在大量出生数的基础上，这些比值并不令人去质疑米兰人中死亡率的一个特殊原因的存在性，那种原因的调查与消除应该是那个国家的政府关心的事情。

如果我们能够成功地减少和消除某些危险和广泛传播的疾病，人口与出生数之比将会进一步增加。对于天花，这一点已被成功地做到了。首先通过这种疾病的接种，然后，通过一种更加先进的方式，即疫苗接种，这是詹纳（Jenner）的发现，这个发现的价值是不可估量的，他因此而成为对人类贡献最大的人物之一。

天花有一个特点，同一个人不会被它感染两次，或者说至少这种情形非常少见，以至于在计算中这种情况可以忽略不计。在疫苗发明之前很少有人会躲过这种疾病，它通常是致命的，它会导致这种疾病的感染者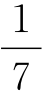的人死亡。有时它比较轻微的，经验显示可以通过为健康的人预防接种而赋予它这种特点，通过适当的饮食并在适合的季节，要使接种的人对这种疾病有所准备。死于接种的人数与所有接种的人数之比不到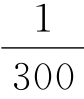。接种的巨大优越性，再加上使人免于毁容以及使人们免遭天花带来的严重后果，使得接种被许多人所接受。有人强烈地呼吁使接种成为常规，但是又遇到强烈的反对声音，因为这几乎总是一件易于陷于麻烦的事情。在这场争论之中，丹尼尔·伯努利提出将接种对于平均寿命的影响化归于概率的演算。由于缺乏在生命的各个年龄阶段由天花所致死亡数的精确数据，他假设感染这种疾病的危险与死于这种疾病的危险在任何年龄都是相同的。在这些假设之下，再加上精致的分析，他成功地将一个一般的死亡表转化为一个如果没有天花或者如果天花只导致感染者非常小的死亡数的情况下也可用的表格，他从中得出结论：接种至少将平均寿命增加三年，这一点在他看来不容再怀疑接种实践的优越性。达朗贝尔反对伯努利的分析：首先是关于这两个假设的不确定性，其次是没有充分地对这一点进行分析，也就是把尽管非常小的即刻死于接种的风险，与比较大但比较遥远的死于自然感染天花的风险进行比较。当考察大量的个体时，这种思考就消失了，因为这个原因，这种思考就不关乎政府，对于他们来说，接种的优势还是存在的。但是，对于一家之主来说，这种情况是非常严重的，如果为他的孩子们接种，他必定担心看到这种情况：他最珍爱的一个孩子死亡并且是这个原因所致。许多父母被这种恐惧所束缚，幸运的是这种恐惧已被疫苗的发现驱散了。通过自然界如此频繁地向我们吐露的那些秘密之一，疫苗对天花的预防就像天花病毒一样确定，没有丝毫的危险。它不会使人感染任何疾病，并且只需要非常简单的护理即可。所以，它的应用立刻传播开来，并使它成为克服人类天然惰性的一个普适的方法，当涉及他们最切身的利益时，必须通过坚持不懈的努力克服这种惰性。

计算消灭一种疾病所产生的好处的最简单方法包括：根据观察精确算出每年死于这种疾病的一个给定年龄的个体数量，并从同一年龄去世的人数中减去它。那么，如果这种疾病不存在的话，这个差与这一给定年龄的人口总数之比就是在这一年在这个年龄去世的概率。然后，将从出生到任何给定年龄的这些概率相加，再从1中减去这个和，余数就是活到那个年龄的概率，它受制于这种疾病的灭绝。这个概率序列将成为与这个假设有关的死亡表，经由以上的论述，我们可以从中得出生命的平均持续时间。这就是迪维拉尔（Duvillard de Durand，1755—1832）发现的平均寿命增加三岁归因于疫苗的接种这个结论的方法。（平均寿命）如此显著的增长将导致人口的大量增加，如果后者在其他方面不受到有关的生存供应衰减的抑制。

人口增长的停滞主要是由于生存供应的缺乏。在动物和植物的所有物种中，自然界不断地倾向于增加个体的数量直到达到平均的供应水平为止。在人类中，道德的原因对人口有着极大的影响。如果易于获得的森林空地能够为新生的一代提供丰富的营养，确定无疑地能够供养成员众多的大家庭，这样婚姻就会受到鼓励并且激励他们繁衍更多的后代。在同样的土地上，人口和出生数应该同时以几何级数增长。但是，当森林空地变得难以获得并且日渐稀少时，人口的增长就降低了。它持续地接近变化的供应状态，这个波动正如一个钟摆一样，其周期由变化的悬挂点所延迟，钟摆通过其自身的重量围绕这个点摆动。估计人口增长的最大值是困难的，经过一些观察之后，情况似乎是在适当的环境中人类的数量每十五年就翻一番。据估计，在北美这个翻番的周期是二十年。在这种状态下，人口、生育、婚姻、死亡率，所有这一切的增长都依据相同的几何级数，可以通过观察两个世纪的年出生数求出这个级数的相邻两项的公比。

死亡表代表了人的寿命的概率，借此，我们可以求出婚姻的持续时间。为了简化起见，假设对于两性来说死亡率是相同的。那么，婚姻将持续一年、两年、三年，或者更多年的概率可以由下列方法求出：构造一些分数的序列，其公分母是表格中对应于结婚伴侣的年龄的两个数之积，其分子是对应于这些年龄加一岁、二岁、三岁，和更大年岁的数的相继乘积。这些分数之和加上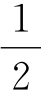就是婚姻的平均持续时间，年为观测的单位。很容易将相同的法则推广到由三个或者更多个体组成的联合体的平均持续时间中去。