在历史视角中的蒯因的逻辑观点

“逻辑”一词显然有多重含义。举例来说，考比（I.M.Copi）和古尔德（J.A.Gould）就在他们两卷本的《逻辑和逻辑理论当代阅读材料》中搜集了很多相关的定义。大家只要扫一扫这书的目录表，就大致可以领教“逻辑”这一名目下内容的林林总总。黑格尔和恩格斯都倾向于在一个宽泛的意义上讨论“逻辑”。在一个与之关联的意义上，意大利人德拉-沃尔佩写出了《作为实证科学的逻辑》（1969，英译本1980）。舒尔茨（H.Scholz）在其《简明逻辑史》（1931，英译本1961）中考察了不同意义上的逻辑。在演绎逻辑和归纳逻辑（或许还加上科学方法）之间，有一种大家都很熟悉的对比。另外，在形式逻辑和辩证逻辑（或先验逻辑）之间，也有一种对比。以前牛津的逻辑教席和现在新设立的数理逻辑教席可压根儿不是一回事。涅尔夫妇（W.Kneale，M.Kneale）的《逻辑学的发展》（1962）所包含的很多内容，一般都会放在“逻辑哲学”的名下。根据这些比较宽泛的逻辑观，蒯因工作的更多内容——若不是所有内容的话——都能够被算作是逻辑工作。

在当下语境中，我将在“数理逻辑”这一更加确定意义上将我的注意力局限于蒯因相关的逻辑工作。即使在这个有限的工作领域中，我也不会考察他对于基础逻辑的不同的雅致表述方式，而首先会考察他构建集合论形式系统的工作。

在我集中讨论蒯因对于集合论的处理（以及这种处理和罗素之间的关系）之前，我还想罗列一下蒯因其他方面的逻辑学贡献。他的一项多年来一直让我感到很佩服，却不为学界重视的贡献，乃是他对于ML所做的的句法学完善。人们经常作出这样的评论，即在一个严格的形式系统中，机器应当能够对证明作出检验。我已经看到了有人曾陈述出这个目标，也有人朝着这个目标努力过。但就我所知，ML是能够满足这一迫切需要的唯一拓展性努力。在这里我想就本书所要包含的内容发表最后一番评论。若我的记忆不错的话，罗纳德•简森曾告诉我说，正是因为读了ML，他才决定不读经济学而改读逻辑学了。为了获得一种更富实践意味的严格性，我在1958年写了一个程序，以便用计算机来证明PM中的所有的基础逻辑定理（请参看我的《纵览》，pp.224—268）。

在ML中，还有对于哥德尔的第一不完备定理的一种处理方案（经由一阶串联理论来进行），而这种处理或许也是史上的第一次。以后，在JSL的一篇写于1946年的论文中，蒯因证明了，这一理论其实是等价于一阶算术的（只不过还得加上加法和乘法这两个原始函数）。在此之后，别人所作出的关于串联的更多细致化考虑也不断发表出来，如斯穆里安（R.Smullyan）在其《形式系统理论》（1961）中的思考。特别而言，有一个问题，可以类比于希尔伯特所列出的问题单中的第十个问题，而这一点最早是由吕布（H.B.Löb）和马科夫（A.A.Markov）大约在1955年提出的。现在就假定有一张字母表仅仅有两个字母构成，如a和b。现在我们就把这些字母串串联起来，以便构成等式。我们还可以加入变项，以便得到词项。比如，对于等式axb=yaab来说，其一个解就是x=aa，y=a。现在的问题是：对于此类等式所构成的所有有穷集来说，是否有一个判定程序，以便判定其可解性？这个问题悬在空中，晃荡了很多年。只不过是在最近，马卡宁（G.S.Makanin）才精心构造出了针对这个问题的一个正面的解。请参看他用俄语写的论文《关于一个自由的半组合的等式》（proc.Of 1978 Int.Congress of Mathematicians，Helsinki，1980，pp.263—268）。关于这个问题更早时候的一些资讯，请参看我的《公众演讲》（1981），p.58。

在20世纪50年代和计算机工程师的接触，使得蒯因发表了好几篇关于真值函项的迅速简化方案的论文。这些成果被人经常引用，而他的诸如“核”和“主蕴涵项”这样的术语日后也被人广泛地使用。蒯因的这些考虑，和最近学界对于可实现的可计算性的研究紧密相关。事实上，自从库克（S.A.Cook）1971年的著作发表以来，P=NP这个等式是否成立的问题，就成为了数学中一个核心的开放问题。这个问题其实是等价于“重言式问题”的，也就是说，是否有“可行的”办法（即在多项式时间中可执行的办法，而非一种关于“实践中的可实现性”的合理化概念）判定一个任意写出的真值函项式子是不是重言式。这个问题也等价于我们在图论、代数和数论等中所看到的很多都已熟悉的问题。最近市面上又冒出一本书，专门概括关于此类一般问题的结果，此即盖瑞（M.R.Garey）和约翰逊（D.S.Johnson）合写的《计算机和棘手性》（1979）。我和杜汉（B.Dunham）合写的一篇论文（参看Annals of Mathematical Logic，1975），在其导论部分曾对此问题作了一些阐述。

为了表述出他所认定的正确用法，蒯因在选择记号和术语方面可谓殚精竭虑。哲学家中现在流行的很多术语都是他发明的，尽管这些术语的哲学用法已经迥异于其在数理逻辑学家中的用法了。有时候这种用法上的分歧仅仅显示了哲学观方面的分歧，如蒯因对于“真值函项理论”（而非“命题演算”）的偏好。有时候蒯因之所以使用不同的术语，纯粹就是因为其谨慎的秉性使然，如他在“蕴含”和“条件”之间，以及在“等价”和“双条件”之间所作的区别。至于他为何使用“否决（denial）”而不是“否定（negation）”，“交替（alternation）”而不是“析取（disjunction）”，也是这个道理。蒯因的术语“量化理论”并未包含同一性，但我们对此术语的更为熟悉的使用却已然包含了同一性，而且也谈论了一阶逻辑（或仅仅是基础逻辑）。当然，在判定某人到底在多大程度上愿意采用日常术语用法的时候，我们所面临的困境要小一点，尤其在没有任何实质性的讨论被牵扯到的情况下。

如果我们想对蒯因的工作和逻辑史之间的关联作出检验的话，那么1940年就是一个比较合适的观察点。那个时候，因为战争的影响，逻辑学的发展停顿了下来。另外，这一年ML的初版所给出的参考书信息也能够帮助我们确定他当时对于逻辑学的熟悉程度。此外，我发现正是从1940年起，蒯因才开始决定将其注意力局限于他在1940年之前就已感兴趣的那部分逻辑学内容上，并致力于深化他对于这部分的理解。直到1940年为止，统治着过去半个世纪的逻辑学界的所有重要的研究方向都已经得到了其坚固的开端。但蒯因即使在那个时候，依然把注意力放在基础逻辑以及集合论的一个单独方面（即其一种别样的表述方式）之上，而这无疑又是因为，仅仅是逻辑学的这些方面，对于蒯因来说才能够产生足够的哲学吸引力（而这显然是就他本人的哲学观来说的）。而我个人很遗憾地看到，恰恰是因为蒯因在哲学家之间所产生的巨大影响，通过蒯因，很多哲学家所获得的关于“逻辑是什么”的观点，恰恰是已被歪曲的。

直到1900年为止，最富影响的逻辑学著作主要已经弗雷格和康托尔（并在次要的意义上为戴德金和皮亚诺）完成了。粗略地讲，弗雷格引入了一阶逻辑，并试图把数学还原为逻辑。康托尔发展出了一个非常有力的集合概念，并引入了无穷数。我在最近付梓的《公众演讲》中曾经论证说，逻辑中的很多核心成果，实际上都是一阶逻辑和无穷序数之间互动的产物，而哥德尔的可构建集，以及很多的模型理论，都可以算作是明显的例证。从1900年到1930年，我们又看到了布劳威尔的直觉主义的出现；我们看到了策梅洛的集合论和对于其的精致化；我们看到了PM和其简化形式；我们看到了希尔伯特的“形式主义”规划以及证明理论；我们看到了勒文海姆以及司寇伦所做出的富有开创性意义的重大贡献；我们看到了希尔伯特-艾克曼的工作的第一个版本，我们还看到了由其他学者所完成的独立成果。这些学者包括：贝奈斯（Paul Bernays）、武卡谢维奇（J.Lukasiewicz）、艾克曼（W.Ackermann）、冯•诺依曼（J.v.Neumann）、珀斯忒（E.L.Post）、屈斯克特（L.Chwistek）、逊芬克尔（M.Schönfinkel）以及拉姆塞（F.P.Ramsey）。

在科学史中，我们不时地会遇到一个某学科得到迅猛发展的短暂时期。比如，在20世纪20年代量子力学发展的就很快，50年代初期往后的十年（或更长时间）内，分子生物学也发展得很快。对于逻辑学来说，这个突飞猛进的时期乃是20世纪30年代。在这个阶段，哥德尔发现了关于基础逻辑的不完备性定理，关于算术和集合论的不完备性定理，得到了一种通过直觉主义算术以及可构建集而完成的对经典算术的解释。赫尔布朗德（J.Herbrand）构造出了关于基础逻辑的一些精巧结构。策梅洛在其1930年的著作中提供了一种很有说服力的对于集合概念的描述，而这种描述其实是为标准的集合论提供了基础。干岑（G.Gentzen）为基础逻辑完善了所谓的“自然演绎”，并给出了两个关于算术的一致性的证明。图灵给出了一个关于理想计算机的非常工整的模型，并给出了令人信服的证明，以保证这个模型抓住了我们关于可计算性的直觉观念。卡尔纳普和塔斯基彼此独立地对真理和有效性概念作出了更切近的研究（这些概念仅在希尔伯特-艾克曼1928年体系中依据直觉而被使用）。

在1934年，哥德尔在普林斯顿研究所上课，在此期间和丘奇（Alonzo Church）、克莱尼（S.C.Kleene）、罗瑟（Barkley Rosser）等人发生了接触，而这些人都在不同方向上对哥德尔的研究成果作出了拓展，并继续通过他们的工作和教学对学界施加影响。而与之作对比，在蒯因的20世纪30年代，和他打得热乎的学者乃是罗素、卡尔纳普以及塔斯基。30年代最重要的逻辑书乃是希尔伯特-贝奈斯在1934年1939付梓的两卷本的里程碑式著作。另外，希尔伯特-艾克曼的著作的一个拓展修订版出现于1938年。在1940年，哥德尔关于连续统假设以及可建构集的那本令人惊讶的形式化单行本（第一版）也付梓了。在前面那个自然段所罗列出的科研成果中的大多数，都已囊括于这些出版物之中。

在大约四十多年以后再回顾1940年，今日的逻辑研究者或许会对那些美好的过往日子心生嫉妒。在那个时候，只要消化掉这么一点点的富有吸引力的研究成果，你就能够在整个广阔的逻辑学研究领域占据前沿的位置。不过，即使在那个时候，大多数逻辑学家依然只能够选择上面所罗列出的有限研究方向中的一些加以精耕细作。在那个时候，以及在更晚的时候，蒯因的兴趣看来就远离了证明理论，以及后来我们所说的递归理论、模型理论，以及计算理论。在集合论的范围之内，他看来并未深入由康托尔和哥德尔所代表的那个传统。对于PM，他当然是烂熟于胸的，对于波兰逻辑学家的一些早期工作，他也是很有学术同情的。弗雷格的著作对他也很重要，但是根据我的揣测，他在1940年对弗雷格的了解，当在对于皮亚诺的了解之下。从1940年或1950年以后，蒯因肯定对弗雷格有了更深入的了解。而根据我个人的看法，弗雷格——而非罗素或卡尔纳普——才是蒯因自己的工作的典范。我曾隐约地记得，在蒯因于哈佛校园的办公室内，弗雷格的照片曾是唯一摆放在那里的肖像。而且我肯定记得他曾以敬重的语气说起过弗雷格。

蒯因的兴趣，并不在于发现集合论中的新定理（即去发现“关于集合的新事实”），也不在于发现那些能够符合不断演进的（但在某种意义上依然是固定的）集合概念的新公理。他甚至不是很在意如何从集合论中推导出标准的结果。毋宁说，他所孜孜以求的，乃是如何找到一个雅致的公理集，以便从中演绎出“日常数学”来。这无疑是弗雷格当年的工作目标，并在一定程度上亦是罗素的目标（他曾非常感兴趣于对于康托尔的无穷数的修复）。但弗雷格也好，罗素也好（至少就其大多数时间而言），他们都在努力探寻那些真的并且是明显的公理。当然，他们没有获得完全的成功。对于蒯因来说，也仅仅是直到前几年为止，他的研究任务毋宁说是如何找到这样一些工整的公理：它们并不明显地包含不自洽性，而且从它们之中，我们能够相对顺当地推导出日常数学来。ML的第六章的总结段落便以一种对于数学的范围来说有些老派的方式表达了此种观点。而此类观点，在蒯因之前和之后都有人表达过。

去评估蒯因的著作对逻辑学的影响，多少有一点困难。从狭义的角度来看，我们恐怕要说，他对逻辑学的影响是微乎其微的。他的NF体系自然激发了很多精巧的工作。他对于其弟子的影响采取了很多不同的形式，但我认为这样说是不过分的，即那些具有比蒯因更宽广眼界的弟子已经在逻辑学领域中做出了更大的成绩。蒯因本人并不想为了一些特殊的目的发明特殊的系统，而那些的确这么做的人（其中很多人都有哲学背景）却很可能从蒯因的著作中学到了很多技巧。当然，当我们转到平时所说的逻辑理论以及逻辑哲学的领域，蒯因的影响就是清清楚楚的。此外，我认为蒯因的逻辑书对于训练计算机程序员是非常有帮助的，因为这些书有助于培养形式精确性（有时候也是人为的精确性）的习惯。而很多学生之所以被挡在专业化的哲学研究的大门之外，恐怕就是因为，他们被研修逻辑学的要求给吓倒了。而蒯因的著作，恰恰是此类逻辑学教材的标准类型。

一个更具实质性的议题则是，一般而言，当一门学科向前发展的时候，其关涉和风格都会发生改变。该现象对于逻辑学来说是更为突出的，因为在短短几十年时间内，它就从一门年轻的学科成长为了一门成熟的学科。特别而言，逻辑学的工作风格已经越来越像数学中的那些传统部门了。除了别的方面以外，这至少已经意味着，对于逻辑学的研究来说，形式精确性的要求现在已经日渐退居幕后了。作为其结果，在很多还活跃的逻辑学家看来，蒯因的工作已然被排除到了主流之外。

对于那些曾经和PM痛苦搏斗过的读者来说（比如我本人在1939—1940年所做的。那时我还在昆明的西南联大读大一），ML的那些基本表达所具有的令人惊异的简洁性和雅致性的确让人印象深刻。在这个系统中，变项可以以任何对象为辖域，而原初的基本词项也只有三个（其一是为了真值函项，其二是为了量化，其三是为了从属关系）。就公认的观点而言，在ML之前，人们知道集合论是可以通过一种简单的记号系统来加以发展的，但从来就没有人曾真的这么做过。若我们从PM开始的话，我们就能够把这种简洁化的努力上溯到屈斯克特（L.Chwistek）在1921年和1922年的工作，以及拉姆塞（F.P.Ramsey）在1925年的工作（详情请参看丘奇的评论，见于JSL，vol.2，1937，pp.168—170）。在哥德尔1931年的著名论文中，我们也可以发现他对简单类型论的一种表述，而这也正是今日我们通常所用的表达。而对比较简单的那类变项的用法则可追溯到策梅洛（1908）。

在1936年，蒯因结束了他的初级研究员的工作，开始以讲师的身份教书。在备课的过程中，他“试图建立一个最合乎情理的全面逻辑系统——或按照今日之说法，逻辑和集合论”。他作出的第一个有趣的努力体现在他1936年的论文中［顺便说一句，在此文中他把司寇伦在1922年的文献误写为1930年，而令人惊讶的是，此误在该论文的1966年再版中依然如故］。在1936年蒯因发表的八篇论文中，只有这篇是关于逻辑的。此外，在JSL杂志的头三年里，他所发表的文章或许超过了任何其他撰稿人。

这个早期的系统S只有一个原初谓词，也就是从属关系。它按照我们所熟悉的方式定义了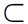和=。除了某种形式的外延化公理以外，唯一的公理图式就是：

（1）EyAx［x∈z≡（xz＆Fx）］

他证明说，简单类型论的基本公理（即省略掉无穷公理和选择公理）的对应物都可以被推导出来。粗略地讲，我们能够从（1）中推导出幂集公理，并证明空集之存在。这样，从空集开始，我们可以从每一个类n出发移至下一个类，其具体的办法则是把类n的普遍集的幂集当作（1）中的z。这样一来，我们就可得到下一类的所有集。

这个系统其实是策梅洛的系统Z的一个子系统（这由Skolem 1922阐明）。关于这个系统，我有好几个评论。第一，（1）是Z中的一个简单公理。其次，很容易证明，我们所熟悉的那些有限集是通过由模型S所构成的空集而被造就的。因此，我们就可证明从S中推导不出无穷公理来。当然，我们可以将某种形式的无穷公理加诸于S。但在那种情况中，我们只是朝向Z以及其更深的拓展形式更近了一步。S还附带地告诉了我们一件事情，即我们能够由此得到一些和集合论公理等价的替代性表述。我本人就曾在几年前做过这些工作（Zeitschrift f.math.Logik，vol.13，1967，pp.175—188）。

对于S中的想法的一种更为神秘和更有趣的发展，乃是几个月之后蒯因对于NF的引用。此系统在1936年12月被提交给美国数学协会，并在1937年2月得到了发表。为了取代（1），蒯因现在放弃了xz，并对Fx附加了很多限制，也就是说，它必须被分层。换言之，它必须能够允许我们把变项的数目置于其中，即以这种方式——仅仅在n∈n+1这种形式的语境中，∈才会发生。这样一来，x∈x也好，x∈u＆u∈x也好，它们都不是分层的。这种做法自然让我想起了类型论的一个做法。实际上，这个做法很像罗素所说的“典型含混性”——但是他之所以引入这种“典型含混性”，主要还是出于一种权宜之计，而并非是对于类型论的一种严肃拓展。斯帕克（Specker 1958，1962）曾证明，NF实质上是等价于类型论再加上合适的典型含混性的公理。而这个做法，非常偶然地提供了一种（具有更好的直观动机的）对于NF的阐述方式——也就是说，它以更为清楚的方式告诉了我们，NF是以何种方式来拓展类型论的。而使得这个清晰表达得以可能的斯帕克的构建工作又被简森所使用，由此得出了一个令人惊讶的结果：NFU（这看上去是对NF的一种轻微的修正）可以被证明为在基础算术中是一致的。NFU仅仅在这个方面和NF相差异：前者有一个比较弱的外延性公理，该公理附加了这个条件：对于“若x和y具有相同的成员的话，则x=y”这个形式来说，x不能是空集。这样一种修正乃是合理的，因为这给非集（non-set）和基本元素留下了空间。而凑巧的是，这种弱的外延性正是蒯因在我们前面提到的系统S中所使用的。

关于NF的故事，在逻辑史中构成了奇怪的一章。一方面，NF是脱离于主流的，而其所导出的结果也只能激起一种边缘性的兴趣。另一方面，的确有一些最棒的数学家的斗志被激发出来，以图回应来自于这种（具有惑人的简单性的）体系的诱人挑战：要么证明这个体系可以导出一个矛盾，要么就去证明它相对于标准体系来说的确是一致的。

蒯因有将著述和教学相互结合的习惯。他在1940年出版的ML就是这种结合的第一个产物。直到1953年，在NF中一直得不到无穷公理——而正是在这一年，斯帕克在NF中证明了选择公理，并由此导出了无穷公理。部分的是出于这个原因，以后蒯因在课堂上所教授的，就是这个被拓展了的NF。在ML的序言中他是这么说的，“这里所呈现的材料，实质上乃是我在哈佛教授的数学19号课程的讲义”。而在此书问世后不久，罗瑟就从其公理中导出了布拉里-弗蒂（Burali-Forti）悖论。蒯因很快就发表了文章予以修补，这些修补以“逐渐加量”的方式引入了集合，而这个做法对于他的书的有限发展来说，其实已足够了。他写道：“我叫出版商印了一张勘误表，夹入我的那些库存未售的书。我在勘误表中给出了一个对于体系的权益的修正方式。勘误表的内容在该书的1947年版本中被正式加入了正文。”也正是在1947年，笔者成功地运用一些更弱的公理，却发展出了比ML所推导出的更多的数学（请参看拙著《纵览》，pp.515—534）。在1949年，我发现，对于那个很麻烦的公理图式*200来说，有一个很自然的替代物。具体而言，我就提出了一个替代性的系统ML。除了这个提议外，我还证明了，若NF是融贯的话，那么ML也是（Wang 1950）。

这种情形能够引起一种更普遍的兴趣。现在就设S为一个被给定的系统。出于方便计，我们就假设S使用的乃是一种单称形式的集合变项，如x，y等。此外，我们再假设能够成为S的成员的都是原初谓词。这样，S就会是一个策梅洛类型的集合论，或是NF类型的，或是前面所说的那种S类型的，或甚至就是ML。在1949年之前，有两种方式来增扩系统S：直谓的和非直谓的。在这两种情形中，我们都把一个新类型加诸于S之上，而具体的办法则是使用另一种风格的类型变项X，Y等——这样，像“x∈Y”这样的式子就能够得到表达了。我们再为这些类加上一条外延化公理。而S的原初变项则被说成是以集合为辖域的。

要形成一个对于S的直谓增扩PS，就得加上这条公理图式：

（P）若Fx没有包含被约束的类变项，则EYAx（x∈Y≡Fx）。

这个做法有个好处，即我们不仅能够把（P）还原为数量有限的特殊事例，而且也能够把我们所熟悉的那些S的公理图式（如分离公理和替换公理）通过单个的公理一一替换掉（如把Fx替换为x∈X）。这正是冯•诺依曼和贝奈斯所发展出来的那种增扩。

对于S的一种非直谓增扩IS则只是一种对于S的二阶理论，或大略地讲，它提供了一种附加补充，即在简单类型论中的一个被截出的部分T_n（对于某个n来说）之后再添加一个更高的类。说得更清楚一点，在被增扩的记号系统中，我们所做的乃是增加这条未被限制的公理图式：

（I）EYAx（x∈Y≡Fx）。

但这样我们也通过允许被约束的类变项出现，而去强化S的公理图式。举例来说，若S是NF，那么就有公理图式EYAx（x∈Y≡Fx）。该图式中的Fx是被分层的。在IS中，这个图式就变成了：

*200Q.若Fx是被分层的，且未包含自由的类变项，则EYAx（x∈Y≡Fx）。

在我们厘清记号差异之后，我们发现，上面这条可以算是原初版本的ML中的一条麻烦的公理。对于自由变项的限制乃是不可或缺的，否则每一个类都会成为一个集合：EYAx（x∈y≡x∈Y）。这个限制在类型论中是不需要的，因为它不是累积的。换言之，在ML的原初版本中，INF就是蒯因的系统。

而我在1949年所做的事情，就是引入了一个新类型的扩增，这种扩增可以说在弱的意义上是非直谓的。说得更清楚一点，要取得对于S的这种增扩（即WIS），其办法是在IS中增加（I），而不是在S中强化公理图式。这样一来，若S是NF，则NF中原来的公理图式就能够保持不变：

*200W.若Fx是分层的且不包含任何类变项，则EYAx（x∈Y≡Fx）。

事实上，ML正是WINF。而对于我证明ML（相对于NF）的融贯性的努力来说，对于*200W的上述限制乃是不可缺少的。

关于NF来说，这么一件事是令人困惑的：若S是一个在策梅洛传统中的标准系统的话，那么将其扩增为IS就不会带来矛盾，且实际上也不会给任何一个具有适当的丰富性的S带来多少新内容。这样一来，INF的不一致性就是指向NF的某些特殊特征的——而这个特征是什么，我认为我们目前还缺乏充分的认识（请参读下一小节）。比起把系统S增扩为IS来说，把系统S扩充为WIS要显得更不自然一点，因为集合（即自然数集或实数集）并没有在WIS中受惠于新增添的力量，而在IS中，它们却得到了。

在检验由NF（并在衍生的意义上由ML）所产生的种种后果之前，现在不妨先让我简要地概览ML（1940，1951）和SL（1963，1969）的实际内容：

ML把超限数全部省略了，推导出了皮亚诺算术的公理以及一些基本定理，并提供了一些关于比率和实数的定义。令人感到奇怪的是，这样的一个集合论系统，在实践上却未包含任何来自于集合论的东西。因此，这也就解释了为何一些更弱的公理也可以满足已然发展出来的这些材料。在1953年，罗瑟在其《为数学家而写的逻辑学》中提供了一种对NF的拓展性发展，但它并不像ML那样精确。如果我们总是要临时性地引入关于无穷公理和选择公理的更为复杂的表达形式（只有在我们需要导出更多的数学内容的时候，这种引入才是真正必要的），那么，NF系统本来所具有的雅致性就会受到很大的损害。

蒯因从1950年春到1959年春的主要学术努力都投入了《语词和对象》一书的撰写。一直到1959年夏，他才重回逻辑领域，并开始写SL，并于1963年1月杀青。而此书的一本深入修订本则在1967年完成，并在1969年付梓。此书分为三个部分。第一部分实际上就是ML的内容，但是表述方式有差异，而且也更为简洁；第二部分处理实数、基数和序数；第三部分则比较了不同的集合论公理系统。这个最后的部分实际上是此书真正的诞生地：这本来乃是蒯因在1953—1954年在牛津所做的讲座的讲义。当年，也正是在准备这些讲义的时候，他获得了一些关于相关内容的预备部分的灵感，并决定着手拓展之。没想到，这些拓展最后占据了此书前三分之二的篇幅。

此书的一个特点就是被蒯因称为“关于类和关系的虚拟论”的东西，而此论和贝奈斯在1937年的某些工作密切相关。第二个特点乃是对于自然数集的一种新定义——此定义省略了对于无穷公理的诉求。具有此特征的一种最早的定义可以上溯至策梅洛在1909年的工作。在1975年，达米特也提出过一个和蒯因类似的想法，而他之所以提出此想法，乃是为了回应我关于“如何找到一种更接近于弗雷格精神的定义”的质询（请参看拙著《纵览》，p.440，p.52）。但蒯因的解答要来得更为简洁。

而弥漫此书的一个普遍特征就是：蒯因一直强调尽可能地将工作局限于比较弱的公理（大多数是存在断言），并在面对“彼此不相容的”公理系统时，做到严守“中立”。我很清楚，现在还很活跃的很多集合论家并不是蒯因这种工作态度的同情者。此外，在他那里，我们也没有直观地看到，怎样的公理对于怎样的目的来说是充分的。新成果——即以前未知的公理——相对于当下手头的目的来说，是可以被证明为充分的。但这一点没有什么可稀奇的。在帕森斯（Charles Parsons）的指正下，此书修订版在处理超限递归的时候祛除了一些原有的瑕疵，而又由于德瑞本（Burton Dreben）的建议，此书添加了一个小节，使得无穷基数得到了一种更为接近日常用法的处理。而替换公理图式的一个特殊情形也得到了专门的提示：一个序数的图像乃是一个集合。若我们假定的那个可构建公理成立的话，我想这也就等价于替换公理了（顺便说一句，“可构建性”的英文是“constructibility”，可是此书在第353页上的索引却将此词误拼为“constructivity”）。

就我所了解的范围而言，自从此书付梓以后，蒯因就再也没有发表过关于集合论的专业论文。事实上，我的印象是，自从1963年以来，蒯因的工作主要是哲学方面的。SL包含了对于他直到1963年初为止关于NF和ML的工作的回顾。在LP的1980年序言里，我们还能够看到蒯因对于新近的集合论研究成果的简评。

自NF问世以来，四十八载已逝。在鲁汶大学，新近（1981年10月）开了一个专门讨论NF的会议。与会者认为，NF提出的主要挑战就是：相对于建立在集合的迭代概念之上的标准集合论而言，如何判定NF是一致的。经过几年的研究之后，大家达成了这样的共识：对于集合论的基本系统而言，无论是NF也好，还是ML也好，都不配成为集合论的基本系统的竞争者。在LP1980年版的序言里，关于在NF和ML中引入自然数和数学归纳的困难，以及这两个系统“允许将自己视为自己的成员的做法（这个做法无疑给个体化投下了阴影）”，蒯因作出了自己的评论。诚然，蒯因在此依然是在强调关于它们的“便利性和雅致性”的“真实”进步。但在我看来，在我们缺乏一种堪比于迭代概念的直观化图景的情况下，以及在缺乏真正的需要来临时增加公理和概念（以求在NF和ML中发展数学）的情况下，蒯因的这种看法着实值得商榷。

在发表NF不久之后，罗瑟发表了两篇论文，在文中他讨论了一些由归纳而来的定义，并解释了那些我们所熟悉的悖论是如何通过哲学定义而被阻止的。NF和INF（即原初的ML中的系统）的第一个确定的成果乃是：

T1.布拉里—弗蒂悖论是可以从INF中导出的（Rosser 1942）。

T2.存在着一种对于NF的有限的公理化（Hailperin 1944）。

既然NF乃是类型论的一个后裔，那么有穷的或无穷的基数和序数的理论就是按照PM的方式发展起来的，而不是按照我们在公理化的集合论中早已习以为常的那种很方便的方式发展起来的。为了导出布拉里—弗蒂悖论，罗瑟推出了这样一些发展。正如我前面曾提到过的，既然我们在自然地把NF拓展为INF后，后者就会成为一个不融贯的系统，那么NF本身就肯定在哪里是不对头的。这种不自然性，部分地是通过如下结果来得到展示的（Rosser-Wang 1950）：

T3.NF是没有什么标准的模型的：和NF的公理相容的对于从属谓词（伴有正确的同一关系）的任何一种解释，都无法使得“少于”关系在序数和有穷基数中得到很好的安排（请参读SL，p.294）。

正如我前面所提到的那样，在1949年我曾证明了：

T4.若NF是一致的，那么ML也是一致的（也就是说，WINF）。用记号来写，就是：若Con（NF），则Con（ML）（Wang 1950）

在1950年，我还提出了一个一般性的论证，由此我证明了：在WIS包含了一种对于算术的合理描述的情况下，WIS中的S是一致的（S是联系于WIS，正如NF是联系于ML的）。在1950年1月，我在谈到一个更大的语境的时候，将该论证告诉了罗瑟。若被运用于NF，则这个论证就能够向我们展示出（请比照拙著《纵览》第十八章）：

T5.NF的一致性在ML中是可证的；或者说，在ML中Con（NF）是可证的。

现在，如果我们把T4和T5联系在一起的话，我们就会达到这样一个结论：在ML中，Con（ML）是可证的。而罗瑟则在1950年春指出了这个令人惊异的论证中的一个小瑕疵，即“表达出自洽性的算术陈述”有含混性，因为在NF和ML中，自然数的表现是彼此不同的。换言之，纵然我们能够在NF和ML（即WINF）中给出一个形式上的类似定义（比如弗雷格版本的），这两个定义依然指涉着完全不同的东西。（在1949年夏天，我向哥德尔解释了我的这个论证，而他的建议是，我应当就这种差异来寻觅我的做法问题之所在。不过我没有理解他接下来所提出的建议。）

在ML中的自然数构成的类Nn乃是具有如下特征的所有类的交集：它们包含零，并对于“后继”这一操作而言乃是闭合的。这样一来，我们就得到了这样一个我们本不想得到的后果（Rosser 1952；SL，pp.306—307）：

T6.若NF是一致的，则ML的类Nn就不是一个集合。

正如蒯因在LP的1980年版序言中所指出的那样，上面这一点指出了ML的一个不那么吸引人的特征，因为对于数学的任何一种实质性发展来说，Nn都得是一个集合。

斯帕特曾告诉我说，他正是因为听了我在苏黎世所作的一次演讲（1950—1951年我在苏黎世），才对NF产生了兴趣。此外，在不止一个场合，他都说过，我写的一个注释对他帮助很大。这个注释是在我的论文《否定类》中提到的（‘Negative types’，Mind，vol.61，1952，pp.366—368。顺便说一句，舍弗也曾引用过这个小注释）。这里我提出的乃是某种处在类型论和NF之间的居间立场。在类型论的类0，1，2，……后面再加上负类-1，-2等，并对它们使用在形式上相同的概括公理和外延性公理。对于每一个类m和正类n来说，我们能够证明，类m包含了比n个集合更多的东西。另一方面，我们也能够证明，在日常数学中该系统是一致的。这个系统要比类型论更为同质化，因为在下述意义上，每一个类都是和任何一个其他的类彼此类似的：每一个类的上和下都有无穷多的类。因此，就存在着一种更强意义上的“典型含糊性”。

关于NF的研究，斯帕特在1953年作出了一个具有决定性意义的进展。这个进展，不仅搞定了关于NF中最著名的关于无穷公理的难题，而且以一种更尖锐的形式向我们呈现了NF中的次序摆放问题。

T7.在NF中选择公理是可被证否的。

既然在NF中，对有穷集而言选择公理是可证的，那么这就隐含了这层意思：在NF中，肯定存在着无穷集。

T8.在NF中我们可以导出无穷公理。

在发表这些成果之前，我曾考虑过海帕琳对于NF的有穷公理化（请参看上文T2）。通过一种合适的选择公理，看来我们能够通过NF中的一个式子来枚举出由无穷多的公理所需要的模型。通过这种方式，我们就能够表述出一条限制公理，其意思是：只有被如此枚举出来的集合是存在的。但这样一来，通过对角论证法，我们也就可以定义出和被枚举出来的集合不同的一个集合了。这样，我们看来就能够获得另一种对于NF中的选择公理的驳斥了，除非新集不是通过一个分层式子而被定义的。这种不清不楚的情形一直维持在那里，但T7是个例外，因为在那里所用的是一条不同的选择公理（Math.Zeitschr.，vol.59，1953，pp.47—56）。既然要获得一种对于分层的直观把握殊为不易，对于NF作出的自然的衍生，最后总免不了要违背事先已经作出的那些限制。

下一个关于NF的精心构造的并饶有趣味的研究成果，又是由斯帕特提出的（Specker 1958，1962；SL，p.292）：

T9.NF是一致的，当且仅当类型论是一个具有典型含糊性的模型，也就是这样一个模型：在其中，对于任何一个没有自由变项的语句p来说，并对于任何一个经由加指数1而从p衍生出来的语句p*来说，p≡p*在模型中为真。

正如我前面所提到的，简森在1969年曾用一系列的有力工具，取得了一个令人惊讶的结果。假设：为了使得x不空（如前面所限定的那样），我们稍微弱化一下NF中的外延性公理，由此我们就从NF出发得到了NFU：

T10.NFU的一致性在日常数学（即基本数论）中是可证的（Jensen 1969）。

在最近几年，又出现了对于上述结果的一些精加工。关于这方面的总结，见于Boffa 1977，并请参看Boffa 1981，在其中他证明了NF的某些子系统的自洽性。不管怎么说，很清楚的是，就对于NF或其他新系统的研究而言，每个人都缄默地使用了策梅洛那种类型论。

在这方面，将NF悬而未决的现状和艾克曼1956年系统所得到的迅速澄清作比照，当颇有趣味。该系统常常通过附加基础公理而得到整理。现在就设由此得出的系统为AS。不久后，列维就证明了AS并不比ZF来得强（Levy 1959）。莱茵哈特（W.N.Reihhardt）又在其论文中证明了ZF并不比AS来得强。后一个结果，以及他对于列维的成果的评论，发表于Reihhardt 1970。在这里，相对的自洽性并不是主要的关涉。毋宁说，两个系统之间的关系以一种更为清楚的方式被呈现出来了，其具体办法是：通过其中一个系统的语句和定理来解释另一个系统的语句和定理。

艾克曼的集合论将我们带向了有趣的“反思原则”和那些被认为是具有哲学吸引力的更强的系统。读者要想了解和这些论题相关的拓展性讨论文献，请参读拙文《大类》（1977）。需要特别指出的是，哥德尔对于此文的贡献出现在该文第325页上。