风险最小化的博弈分析

如果分出公司和接受公司追求最优化的目标是使双方风险最小化,那么如何确定风险互换比例才能达成最优再保险合约成为又一个问题。

假设保险公司1和保险公司2签订一个风险互换的成数再保险协议。保险公司1分出的比例为α,保险公司2分出的比例为β。双方希望风险互换后的目标是尽可能地缩小各自的风险分布方差,而不是增加各自的期望收益。显然存在许多的(α,β)使两家保险公司都能降低方差,问题是有些(α,β)更有利于保险公司1,有些(α,β)更有利于保险公司2。在双方达成合作协议的过程中,都希望尽可能地使协议有利于自己。为此,双方之间将存在一个讨价还价。这个博弈充分体现了局中人的目的部分是为了合作,部分又引起了冲突与矛盾。

局中人1——保险公司1;

局中人2——保险公司2;

p1——保险公司1方差的缩减量;

p2——保险公司2方差的缩减量。

局中人1和局中人2通过合作谈判,确定合适的(α,β),使各自的p1和p2尽可能地大。

假定局中人1的赔款为X1,期望值为E(x1),方差为V(x1)=V1＞0;局中人2的赔款为X2,期望值为E(x2),方差为V(x2)=V2＞0。局中人1和局中人2的风险互换是线性风险互换,局中人1分出的比例为α,局中人2分出的比例为β。双方风险互换后,局中人1的赔款为Y1,期望值为E(y1),方差为V(y1);局中人2的赔款为Y2,期望值为E(y2),方差为V (y2)。风险线性互换公式为:

这里的K是一个固定的数,可以是正的,也可以是负的。X1与X2相互独立,易知:

E(y1)=(1-α)E(x1)+βE(x2)+K

E(y2)=αE(x1)+(1-β)E(x2)-K

V(y1)=(1-α)2V1+β2V2

V(y2)=α2V1+(1-β)2V2

保险公司1和保险公司2的方差缩减量分别为:

p1=V1-(1-α)2V1-β2V2=2αV1-α2V1-β2V2

p2=V2-α2V1-(1-β)2V2=2βV2-β2V2-α2V1

给定保险公司2的方差缩减量为常数C,使保险公司1的方差缩减量达到最大的方程为:

s.t. p2=2βV2-β2V2-α2V1=C

构造Lagrange方程:

L=2αV1-α2V1-β2V2+λ(2βV2-β2V2-α2V1-C)

=(2-2α-2αλ)V1=0

=(2λ-2β-2βλ)V2=0

由以上两式可得:

α+β=1 (3-1)

因此,当(α,β)满足α+β=1时,两个保险公司的方差缩减量达到了Pareto最优,这些满足α+β=1的全体(α,β)点构成了一条Pareto最优曲线,暂记为V(12),这时,

p1=V1-(1-α)2V1-(1-α)2V2

p2=V2-α2V1-α2V2

在上式中消掉α,可得V(12)的函数形式为:

可行集合F是由V(12)和p1≥0、p2≥0所组成的闭凸域,用数字形式表达其范围为:

纳什讨价还价解(α,β)在约束条件α+β=1下使纳什积p1p2达到最大,即:

可得:

由式(3-4)可得α,进而求得β=1-α。

通过特例予以说明。

令:E(x1)=5,V1=4,E(x2)=10,V2=8,K=5α-10β。

则:E(y1)=E(x1)=5,E(y2)=E(x2)=10;

假如取点S1(α,β)=(0.2,0.3),则(p1,p2)=(0.72,3.92);

又取点S2(α,β)=(0.4,0.4),则(p1,p2)=(1.28,4.48)。

毋庸置疑,点S2比S1使双方的方差缩减更显著。如果再取点S3(α,β)=(0.53,0.47),相应的方差缩减量为(p1,p2)=(1.349 2,4.629 2),则点S3比点S1和点S2又更进步,很显然点S3是Pareto最优曲线V(12)上的点。

Pareto最优曲线V(12)为:

可行集合F为:

从式(3-4)得:2α3-3α2+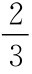=0,易求得三个根1.304、0.613和-0.417,因此,纳什讨价还价解为:

α=0.613,β=0.387,p1=2.203,p2=3.491 (3-7)

两家保险公司之间互换风险方案的确定相当于关于“盈利”(方差缩减量)分配的讨价还价。如果两家保险公司不合作,方差显然不会减少,因此双方意见不一致的点为(0,0),两家保险公司最理想的点是完全缩减方差,即(4,8)。从图3-1中可以看到,在点S1、点S2和点S3中,点S3位于V(12)上。

图3-1 风险互换求解示意图

卡莱—斯莫罗廷斯基解应该是Pareto最优曲线V(12)与连接(0,0)、(4,8)两点的直线的交点,即有p1︰p2=4︰8,利用V(12)的参数式(3-2),有:

解得:

α=0.585 786 43, (p1,p2)=(1.941 125 42,3.882 251 1)

可以发现,对于局中人2,卡莱—斯莫罗廷斯基解要比纳什解更满意一点,这是因为卡莱—斯莫罗廷斯基解的结构考虑了局中人2的方差缩减理想值比局中人1的理想值大得多的原因。

本特例中一个有趣的解是(p1,p2)使(p1+p2)达到最大值,容易求得α=β=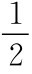,p1=1和p2=5。这样的结果总体效果相当不错,但是局中人1的缩减量显然不及局中人2,其实,通过“再谈判”,由局中人2给予局中人1“适当”的补偿也许是最理想的结果。

在完全信息条件下,假定每一家保险公司都对自己和另一家保险公司的风险状况具有完全充分的认识,这意味着在再保险合约谈判中一方不会向另一方隐瞒信息,并且双方对于所有可能的信息取得了一致的评价。毫无疑问,这是一个理性的假定。

正如表3-1中所显示的保险公司1和保险公司2的最大效用函数的图形,被假定为两家保险公司所了解。但这可能是一个危险的假定,在再保险合约的谈判中,任何一方都无法阻止其谈判对手隐瞒实情的动机,因为这会给隐瞒者带来很大好处。

对这一点可以用以上已举过的特例来说明。保险公司1的效用函数是u1(x)=-a1x2+x,那么,很清楚,a1越小,保险公司1的风险就越小。在a1=0的限制条件下,保险公司1就根本不必考虑风险,其唯一目标就是使其预期利润最大化。

在特例中假设保险公司1和保险公司2对风险的真实态度a1=a2=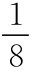,但如果保险公司 1 能将它的效用函数表示成a1=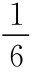,这实际上就意昧着保险公司 1 假装承担的风险要比真实情况大得多,并且对其向保险公司 2提供的再保险保障需要一个较高的补偿。如果保险公司1的这种假象行骗能够成功,且两家保险公司也通过某些理性的讨价还价过程做成这一笔对双方可能最好的买卖,那么相应的解将是以a1=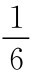和a2=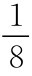获得。根据前面已经给出的一般公式,其纳什解近似地等于:

从表3-1可见,相对于真实条件a1=a2=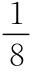来说,上述解Q=-0.5就使保险公司 1 获得比 h=和Q=-0.5时更高的效用,即保险公司1的效用由8.19提高至8.75,保险公司2的效用由13.19降至12.75。换句话说,保险公司 1 通过隐瞒真相从保险公司2赚到了一笔钱。

很显然,在再保险的实际交易中欺骗对手的情况还是客观存在的,所以,不完全信息下再保险合约的最优化问题仍然是分出公司和接受公司面临的现实问题。