衍生产品定价

第20章　衍生产品定价

投资新闻20

FT

诺贝尔委员会的新闻稿

1997年，瑞典皇家科学院决定将诺贝尔经济学奖授予瑞典银行的美国剑桥哈佛大学的教授罗伯特·C.默顿（Robert C.Merton），和美国斯坦福大学的教授迈伦·S.斯科尔斯（Myron S.Scholes），表彰他们找到了确定衍生产品价值的新方法。

默顿、斯科尔斯与后来的布莱克一起发展了股票期权价值的首创公式，这种方法为许多领域的经济股价铺平了道路。它还生成了金融手段新的类型，以及促进了社会风险的更有效的管理。

这一年的桂冠得主，默顿和斯科尔斯，曾经与布莱克一起发展了这种方法，布莱克在1995年逝世，年仅55岁。三位学者研究的是同一个问题：期权定价。1973年，布莱克和斯科尔斯发表了后来被人们所知的布莱克—斯科尔斯公式。全世界每天有成千上万的交易商和投资商使用这个公式在市场中给股票期权定价。默顿设计了来自于这个公式的另一种方法，并且已经表现出广泛的应用性，他在很多方面推广了这个公式。

所以布莱克、默顿和斯科尔斯为过去10年中的市场迅速增长打下了基础，他们的方法已经具有更加普遍的应用性。但是，也创造了新的研究领域，包括金融经济的内部和外部。相似的方法可以用来为保险合约和担保定价，或者是有形投资工程。

布莱克、默顿和斯科尔斯的方法在许多经济问题的分析中已经是必不可少了。衍生证券形成了一种特殊的情况，也就是所谓的或有债权，定价方法也经常用于这种比较广泛的合约的级别。公司中股票、优先股、贷款和其他债务手段的价值取决于公司的整体价值，这与股票期权的价值取决于指定股票的价格在本质上是一致的。桂冠的得主们已经在1973年发表的文章中对此有所观察，所以为公司负债定价的统一理论打下了基础。

银行和投资银行有规律地使用这种方法为新的金融手段定价，并且为它们的顾客的具体风险提供量身定做的手段，同时这样的机构也能够减少它们本身在金融市场中的风险暴露。

资料来源：新闻稿:1997年诺贝尔经济学奖。经许可引用。

学习目标

在完成本章的学习后，你应能够：

1．运用期货定价方程。

2．区分期权价值的界限和使用买权与卖权的平价关系。

3．使用二项式树形图计算期权价值。

4．使用布莱克—斯科尔斯的期权定价模型（BS模型）为买入期权和看跌期权定价。

5．讨论关于期权定价的实际问题。

这一章涉及期权定价和投资商如何确定衍生工具是低估还是高估。这一直以来就是一个令人头痛的问题，但却有着重要意义，正如在《投资新闻20》中阐述的那样。默顿和斯科尔斯在1997年由于对期权定价的贡献获得了诺贝尔经济学奖。布莱克是布莱克—斯科尔斯期权定价模型的合著者，他为具有突破意义的期权定价模型作出了贡献，但是却没有能够等到接受诺贝尔奖的那一天便英年早逝了。

衍生产品定价基本上是依靠无套利（No-arbitrage）规则，即在平衡的状态下，没有套利利润盛行。回顾一下以前的知识，同样的规则在第11章中使用来得到套利定价理论（APT）。这个方法与在第13章用来为证券定价和在第15章为股票定价采用的观点不同：为了这些现金流量的风险以合适的利率来贴现未来现金流量。可以看到，当应用贴现的现金流量方法时，有两个主要的任务：预计未来现金流量（因为，公司的收益）和决定如何纠正现金流量风险的贴现率。对于为证券和股票定价来说，这些任务已经很困难了。对于为衍生产品定价，问题就更严重了：首先，衍生产品有可能很不稳定，要得到期待的未来现金流量的正确预计是很难的；其次，对于衍生产品，没有现金流量的连续的风险调整贴现率，因为衍生产品的风险会剧烈地改变，例如，指定资产的价值或者是到期日的事件发生变化。由于这些原因，研究集中在不要求贴现有风险的现金流量的方法上，即在无套利规则基础上的定价。

所以，理解衍生产品的价格行为要求衍生产品套利的指示。第11章中曾经讲过，套利的机会意味着今天的零投资只能获得未来非负的支付。^[1]换句话说，存在不需要面临风险就可以获得利润的机会，并且这个机会是可以免费获取的。^[2]在平衡的状态下，套利机会是不存在的；所以套利利润的存在代表的是不平衡。然而，当套利机会可得的时候，它们持续的时间也不长。通过今天的电脑科技的可用性，投资商需要快速地开发套利机会；每个人都想利用它们，因为套利基本上属于“免费的午餐”。衍生产品价格的大部分是由衍生产品交易商消除套利机会来确定的。

为了理解这一点，看一下使用衍生产品获利的套利交易意味着什么：假如股票（执行价为21美元）的买入期权的价格为3.00美元。股票值15美元，看跌期权（执行价也是21美元）值7美元。期权为欧式期权，一年后到期。利率为5%。存在套利机会。特别是，投资商可以获得套利利润，如果他/她^[3]出售买入期权；^[4]借入20美元；③购买一支股票以及④看跌认沽期权。今天的现金流量为$3+$20=$23，今天的流出量为$15+$7=$22，这样就引起了今天的净现金流量为$23－$22=$1。但是，我们来看看在到期日的时候发生了什么：净支付为零！可以用第19章的收益图来检查一下。

所以，投资商可以不用面临任何风险而获得1美元。很清楚地，这位投资商不会只使用一次这个策略，而是尽可能经常地使用。利润是无止境的——只要这样的价格盛行。很明显，没有风险的无限利润是很受欢迎的，所以更多的投资商会使用这种交易策略。但是随着量的增加，价格将会进行调整。买入期权的大量销售将会引起价格的下降压力，而看跌期权的购买将会提升价格（其他的工具也会有所反应，但是假设在一段时间内只有期权价格作出调整）。结果，利润下降。只要仍然有利润产生，这个过程就会继续，所以在最后，价格将会是相同的。实际中，调整的过程仅仅在几分钟或者几秒钟之内就可以完成。

以上的例子表明无套利的概念是定价证券的有力工具。只要以知道的价格使用手段可以复制工具，那么套利将会保证工具的价格与合成复制品的价格相同。^①因为，如果我们知道这支复制的资产组合的构成，就可以知道任何工具的价值。这个方法对于定价衍生产品来说尤其强大，因为它们是从几乎一直交易的指定资产得到的价值。这就使得构建复制的资产组合相对简单了——我们需要的只是指定资产借入或借入货币的能力，为此使用无风险的工具。注意，我们不使用贴现现金流量的方法，所以能够避开确定风险调整贴现率的问题。相反地，只是依靠无套利规则，它说明的是工具的价值，并且它的合成复制品应该是一样的。

这一章其余部分将会考察不同的衍生产品的定价。首先要介绍一些必要的术语，接着讨论期货合约的定价，也会提供关于掉期和远期协议（尽管没有详细的讨论）的蓝图。期货定价集中在所谓的持有成本模型上。在期权定价上，先要考察所有期权价格都必须满足期权定价界限，期权价格仍然在界限之内是因为市场中的套利力量。然后是二项式模型。接着转到了连续的时间，学习布莱克—斯科尔斯定价方法来确定期权和它的进项的平衡价格。最后，我们考察的是与BS模型相联系的实际问题。

注意这一节期权方面大部分的例子与定价股票期权相关，但是，在这一章说明的同样的原则可以应用于任何指定资产期权定价，例如，股票指数期权、期货期权以及外汇期权。

20．1　静态与动态对冲

为了帮助理解这一章的资料，在构建套利的两种方法之间作出区分是有帮助的。第一种方法使用的是资产组合，在原始购买之后，由于构建（涉及工具的收益模式）它仍然是没有风险的，这叫做静态对冲（Static Hedge）。^②原始的资产组合在整个投资范围内是没有风险的，所以静态对冲不要求进一步的交易。第二个方法是一系列的交易，制造了这样一种资产，那就是在每次价格运动之后为了保持无风险必须要保持结余，后者是动态对冲（Dynamic Hedge）。

我们在期货定价中将会遇到静态对冲的例子，在期权定价中静态对冲和动态对冲的例子都会遇到。区别并不是巧合的：动态对冲被要求制造“合成衍生产品”，其中的衍生产品的收益轮廓是指定资产价值的非线性作用。如果衍生产品和指定资产有同样的收益模式，那么静态对冲就足够了。如果它们的模式不同，比如说期权（比较股票的线性收益与第19章描述的期权不对称收益模式），那么就需要动态对冲。每次指定资产的价格发生变化，人们需要重新计算构成套利（或者对冲）资产组合的股票和票据的比例，并且要相应地卖出或者买入资产。在期权定价中的唯一例外就是在以上例子中描述的情况，需要使用一个期权来制造另一个期权的静态对冲。

实践中，动态对冲还用于风险的操控，作为衍生产品的备选或者补充，在第21章中将会有所说明。但是，在1987年10月的套现期间，许多使用动态对冲的投资商不能以足够快的速度和足够多的数量进行交易来维持他们的对冲。另外，由动态对冲引起的大量销售——根据一些观察家的说法——又增加了现金，因为在价格下降的时候售出股票，导致进一步的下跌。许多市场的现行实践是大部分投资商使用期货协议而不是指定资产本身来制造动态对冲，因为期货协议可以在需要大量公开的时候提供较大的流通性。

20．2　期货定价

这一部分涉及期货协议的一般定价模式。^[5]期货价格很少与即期资产的现行价格相同，在大多数时间里，当与跨越到期日相比的时候，期货价格有着很清楚的模式：任何指定资产期货价格几乎总是在所有到期点的上方或者下方。但是为什么这个模式在不同的指定资产之间有所区别呢？怎么能够解释S&P 500指数提前到期的期货无一例外地低于其价值？如果在无套利原则的基础上，期货协议应该拥有的价格又是多少？定价期货协议的能力在许多方面都是有用的。投资商能够评估现行的期货价格是否合理，以及相应地调整他们的资产组合。另外，甚至当期货没有被投资商买入或者售出的时候，期货价格包括利率和汇率等有用的信息。

20．2．1　定价股票指数期货

期货协议在到期之前的价值是多少？来看一下S&P 500指数期货协议的细节。回顾以前的知识，S&P 500指数是500支普通股的价值加权指数，其期货协议是现金支付的，如第19章描述的那样。

可以为这个期货协议制造套利资产组合。考虑以下的策略：借入S₀+m，其中m是期货协议要求的保证金，S₀是现行的估价。使用这笔资金来购买这支股票（S&P 500指数），并且卖空期货协议（要求保证金m），原现金总流量为零。借入是在实现预定的期间内的——直到期货协议到期。我们来看到期日又发生了什么。要求支付贷款的现金流量为－（S₀+m）（1+r），其中r是相关利率。股票生成了现金流量S_T+D，其中S_T是这个时间最后的股价，D是支付的股息。^[6]短期期货协议要求支付保证金m，由此得到利息，所以在这段期间之后的现金流量为m（1+r）加上卖空合约的盈利或者损失。到期时，现货价格与期货价格相同，所以期货后半部分的现金流量为F₀－S_T，其中F₀是现行期货价格。^[7]

如表20.1所示，通过金融策略的构建，当天的总现金流量为零。为了避免套利机会，来自三个投资（贷款、股票和期货协议）的总期货现金流量一定也是零，即：

F₀－S₀（1+r）+D=0

或者：

F₀=S₀（1+r）－D

因为D/S₀（也可以用下面的d表示）是股息率，我们得到：^[8]

总的说来，期货价格是现行指数价值、无风险利率、股息率以及到期时间的函数。这意味着期货价格等于现货价格加上拥有即期资产的净利润。也就是说，如果S&P 500指数由借入无风险利率购买，那么相关期间的金融成本为r。但是，事实上拥有S&P 500指数的证券给了投资商能够减少这些金融成本的股息流动。当术语发展的时候，这些经常为负的利润（商品期货就是这种情况）以及这些净利润通常被描述为持有资产的成本（Cost）。由于这个原因，方程20.1经常被称为持有成本模型（Cost-of-carry Model）。

有趣的是，关于期货价格的期望并不进入期货定价的方程，除了通过S₀。如果是现行的市场情况，现行的价格是（贴现的）期货价格的最好预计，否则价格当天将会改变——又是因为没有套利。^[9]

所有的合约都可以用相似的方法进行估价，唯一的区别在于拥有（持有）指定资产的成本。在股票指数的情况下，拥有指数的成本是无风险利率（金融成本）减去股息率（来自资产的现金流量）。例如，假设慕尼黑国际博览集团的股息率为3%。无风险利率为5%。^[10]

表20.1　确定股票指数期货的平衡价格

资料来源：利维：《投资学入门》第二版。

再假设慕尼黑国际博览集团现在为1045美元，6个月的期货协议期以1085美元进行交易。所以，1085>1045（1+0.05－0.03）^1/2=1055.4，套利盈利是可以得到的。考虑遵循表20.1的交易策略。购买指定的MMI（通过直接购买指定证券或者效仿MMI的共同基金）；售出要求附息保证金的期货协议期；最后，借入保证金和MMI价格（1045美元）。所以，原始现金流量为零。从表20.1我们知道这个策略将在未来产生正现金流量（零投资）为1085－1045（1+0.05－0.03）^1/2=29.6MMI的每个单位。

这个活动将使期货价格下降，指数价值上升。套利者通过交易价格差异在使证券市场变得高效方面有着很重要的作用。注意在实践中，套利者是要面对一些风险的，比如说错误估计股息率或者现行利率的风险。

20．2．2　定价货币期货

货币期货可以通过和指数期货一样的方式来定价，除了持有成本是国内无风险利率（r_L）和外汇有风险利率（r_f）之间的差别。表20.2表明的是可以在外汇期货得到平衡价格的策略。货币期货和指数期货基本的区别在于，假设对于货币期货，得到的是外汇无风险汇率，而在指数期货的计算中，假设得到的是股息率——当即期外汇被购买的时候，这个总数应该投资在外汇无风险资产中。

表20.2　确定外汇期货的平衡价格

资料来源：利维：《投资学入门》第二版。

表20.2说明了金融交易的细节，当天这些交易的成本，以及套利策略在合约到期时的现金流量。再一次地，m美元的保证金假设是在期货交易方面，这个例子是用英镑作为外汇，美元作为本国货币。

首先借入1美元，按照现行的汇率（S₀）它可以提供S₀美元的现金流量。例如，如果汇率是0.625英镑/美元，那么借入1美元将提供1.60美元（=1/0.625），S₀为1.60。那么需要支付1+r_f英镑，其中r_f为英国银行对于相关的交易期间的外汇无风险汇率。但是，因为一年内汇率将要成为S₁美元/英镑，美元的现金支付为$S₁（1+r_f）。

在美国借出S₀－m在将来得到（S₀－m）（1+r_L），其中r_L是相关时期内本国货币利率。最后，购买期货买入1+r_f英镑；当天我们支付保证金m，下一年得到利率m（1+r_L）加上期货交易的利润（1+r_f）（S₁－F₀）。

没有套利利润，这个时期结束的现金流量一定为零。所以：

其中S₀和F₀是对于本国货币来说的外汇的一个资产的现货和期货价格。^[11]持有的成本为（1+r_L）/（1+r_f），是指定资产每1美元的价值。注意，如果在到期的时候所给的是不同时间的利率（例如，合约只有半年到期，给出的却是年利率），那么需要因此改变公式为（1+r_L）^t/（1+r_f）^t，其中t为到期日，给出的是这段时间的一部分利率。

练习栏

问题假设一个人是瑞士法郎外汇交易的套利交易商，在汇率的大变化之后，观察到如下的信息：S₀=$0.65/SwF（美国美元和瑞士法郎之间的外汇率），F₀=$0.64/ SwF（外汇期货价格），r_L=3%（美国年无风险利率），r_f=6%（瑞士年无风险利率），t= 0.5年。这些价格是处于平衡状态吗？如果它们不平衡的话，这个人怎么才能获利呢？

解答要看这些价格是否处于平衡状态，要计算理论的期货价格并且将其与实际的期货价格进行比较。所以：

结果要高于现行的期货价格$0.64/SwF。所以，期货价格相对于现货价格来说太低了。在这种情况下，表20.2建议的套利交易就会导致如下的当天现金流量（见表中的“净仓量”）：

S₀（1+r_L）-F₀（1+r_f）=（$0.65/SwF）（1.03）^1/2-（$0.64/SwF）（1.06）^1/2≈0.00076

这个策略将会导致0.00076的正现金流量和将来没有现金流量（注意期货协议的买方和卖方都必须要放置保证金）。

外汇期货市场在确定利率的不同方面也有帮助，如下面的练习所示。如果暗示的利率与观察到的利率不同（或许是因为不能维持的外汇政策），投资商可能会对这样的市场产生兴趣。^[12]

练习栏

问题假设1997年12月英国英镑期货协议以1.6664美元/英镑支付，1998年3月合约以1.6604美元/英镑支付。在这段时期内英镑和美元之间的隐性利率差是多少（假设两个国家的收益曲线都是平的）？

解答从方程20.2知道：

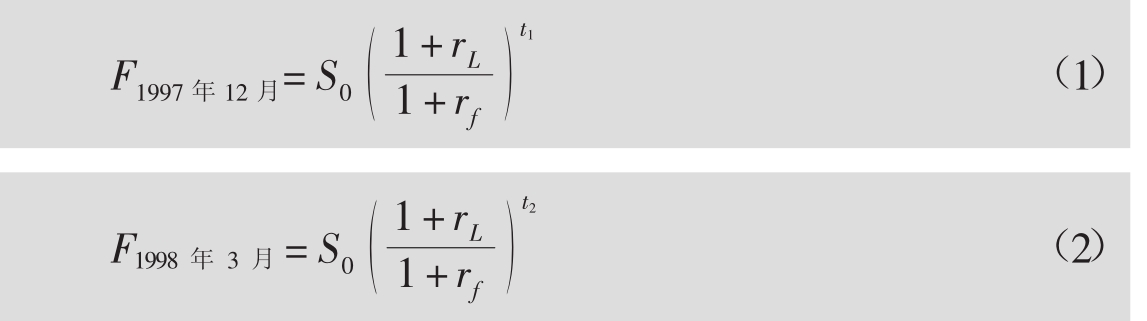
用方程2除方程1得到：

因为合约是三个月份支付的，用t₂－t₁=3/12=1/₄。替换期货价格就得到下面的式子：

所以：

美国美元和英国英镑之间的隐性利率差为－1.43%。

20．2．3　定价商品期货

表20.3表明的是商品期货交易。为了给商品期货估价，需要考虑到具体商品的持有成本的两部分：存储成本和保险成本，用C代表。在这里，S₀是商品的现行价格，F₀是商品的期货价格。S_T是商品的未来价格，m是期货交易要求的保证金。再一次没有套利利润暗示着如下的内容：对于指定资产的拥有仅仅是为了消费目的的商品期货，就像人们要投机商品期货一样，方程20.3有一点小的变化，即为：

F₀≤S₀（1+r）+C

如果F₀＞S₀（1+r）+C，那么无套利观点仍然认为，在1+r下购买S₀+C，套利者可以借需要的数量，卖空期货协议。但是如果F₀＜S₀（1+r）+C，那么可以仅仅通过卖出指定资产和收购期货协议来获得套利利润。指定资产的拥有者会很不情愿地这样做，因为他们为了消费目的拥有指定资产，他们所拥有价值或许要高于可能的套利利润。

回顾以前的知识，拥有股票指数期货的投资商收到股息，所以金融成本被红利的利润所减少。一方面，拥有商品期货，另一方面，存储成本是持有资产的额外成本。

表20.3　确定商品期货的平衡价格

资料来源：利维：《投资学入门》第二版。

20．2．4　基价

回到这一节开始时的问题：怎么解释与现货价格相比的期货支付价格模式，尤其是当期货价格在现货价格之下的时候？那就是持有成本。使用方程20.1，但是把d理解为总持有成本：观察S₀和r，以及估计d，期货的价格F₀可以表示为：

F₀=S₀（1+r－d）

如果r>d，那么r－d>0且F₀>S₀，如果r<d的话，相反也是正确的。因为d可能是正或者负，取决于指定资产，我们能够解释在现货价格之上或者之下的期货价格。

但是从业者经常从一个不大一样的角度来看持有成本：他们计算的是基价（Basis）。基价是现行的现货价格和期货价格之间的差别（这与基本点的概念是完全不同的）。特别是：

基价=现货价格－期货价格^[13]

B_t=S₀－F_0，t

其中B_t代表使用在时间t到期的期货协议的基价，S₀是现行的现货价格，F_0，t是在t到期的期货协议的现行期货价格。在期货协议的有效期中，基价是发生变化的，有可能为正，有可能为负。第一种情况叫做（现货）延期交割（Backwardation）（也称为标准市况）；另一种情况则被称为交易延期（Contango）（也被称为逆转市况）。但是有一点是确定的，在到期日之前，基价将会变成零（如果到期的期货价格不同于现货价格，就存在套利机会），这个过程叫做聚集（Convergence）。

因为这一特点，基价可以在不同的交易策略中应用。人们可以在这个基础上投机，意味着投资商卖空比较昂贵的然后购买比较便宜的，生成原始现金流量，但是到期的时候，净现金流量将会是零。如果指定资产具有不可忽视的持有成本（仅仅补偿基价），这样的策略就不那么具有收益性了。如果是那样的话，这个策略最好描述为持有成本的套利。基价在对冲中也很重要，因为如果合约必须在到期前流通，那么基价就会引起意想不到的损失（或者盈利），因而要降低对冲的质量。

基价和持有成本之间有关联，但是它们的影响是不同的：当考察持有成本模型的时候，它通常是关于现货价格的一个乘法术语，但是基价却总是一个加法术语。意思是说基价也许会改变（以美元的形式），但是持有成本却保持不变（指定资产的每个单位）。另外，实际的持有成本在投资商之间会有所区别，因为在实际中不是每个人都面临着同样的利率或者存储成本。基价可以仅仅以市场的数据进行计算，但是持有成本（稍微）是确定到投资商的，在这之上建立交易策略就不是特别的可信了。

20．3　期权定价：界限

即使仅仅通过观察期权到期时的价格来评估期权的价格，也已经能够下结论说期权不会有任何价值；它们的价格必须在一定的界限之间。这些期权定价界限（Option Value Boundaries）在为寻求理解期权价格提供了进一步帮助，因为如果价格不能满足界限，那么投资商就可以获得套利利润。这一章说明了套利活动会使期权价格很快地进入界限中。

另外的优点是这些界限是不受收益率分配的影响的。在期权的有效期内支付的股息没有任何影响。决定期权价值（而不是界限）的模型总是依赖于分配的假设，尽管它们都来自于无套利规则。期权定价界限是我们所能给出的不用制造更多假设的最好的答案。

为了说明这些界限，考虑表20.4，这是做市商Unilever公司的假设报价表。这些价格是否合理呢？期权有没有高估呢？是否有低估呢？找到期权界限会给这些问题一个初步的答案。

20．3．1　买入期权界限

对于买入期权，现行价格有上方的和下方的界限。而下方的界限：欧式期权（c₀）的价格必须要在下方的价值之上：^[14]

表20.4　Unilever公司股票的收盘价及期权

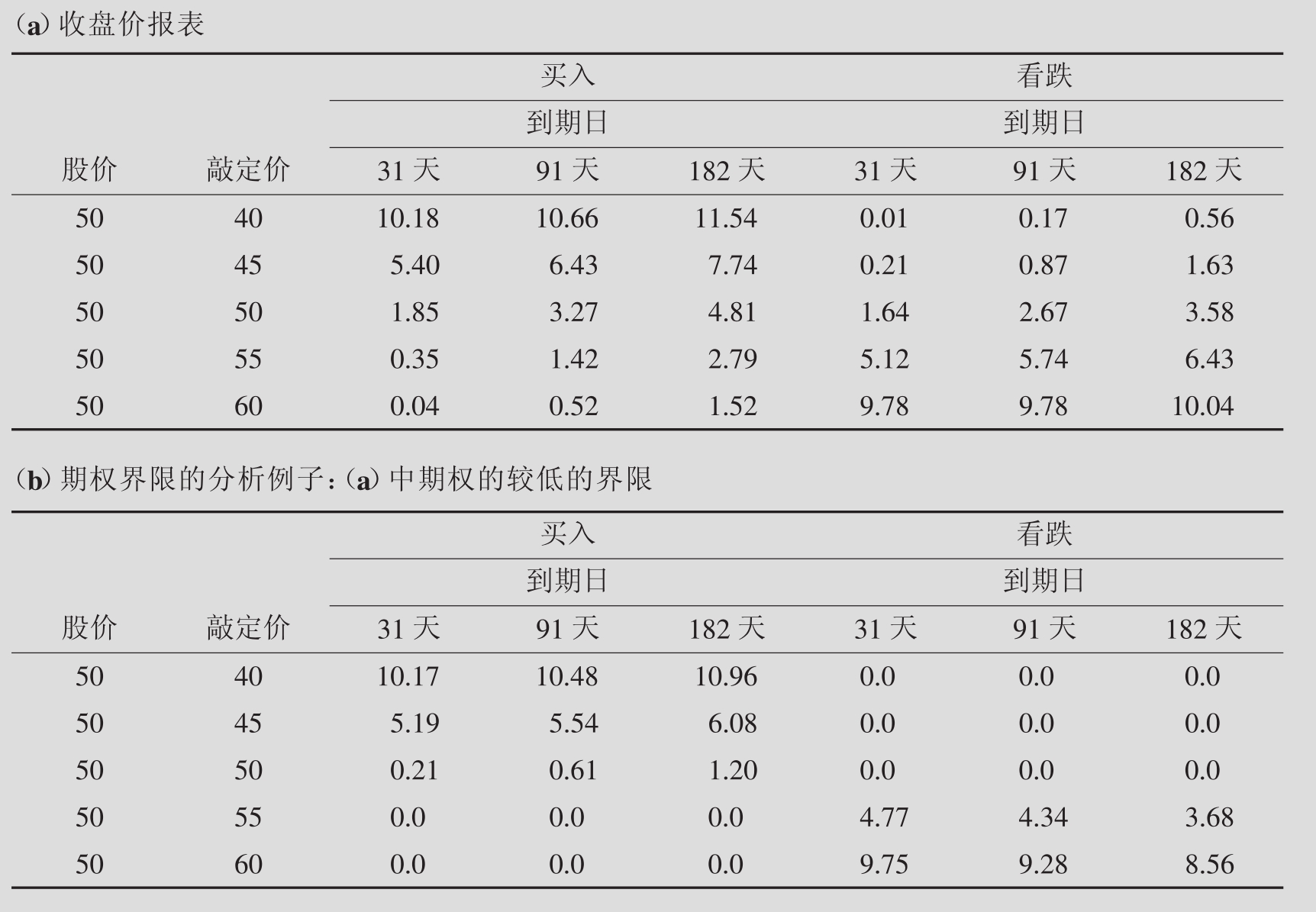
资料来源：利维：《投资学入门》第二版。

其中S₀为当天指定资产的价格，X是执行价，t是到期日（年的分数形式），r是年无风险利率，这个被认为是不变的。所以，价内买入期权或者仅仅是价外[S₀>X/（1+r）^t]，价值总是严格地为正（因为期待的股价将是现行股价加上增长r）。如果期权远远地在价外，以至于到期日期待的价值仍然还比敲定价低，界限为零，仅仅因为期权持有者拥有买的权利而不是义务。

为了说明方程20.4，我们考虑一下在表20.5中的交易策略（假设任何交易都是以0开始，到t结束）。注意未来分成了两种可能：S_t≥X和S_t<X。关于S_t的精确价值的更多信息是不需要的。

表20.5的第一栏确定了在时间0的精确的交易策略。第二栏到第四栏包括如果为正的现金流入以及如果为负的现金流出；数量是基于第一栏的交易策略的。回顾以前的知识，当投资商卖空股票的时候，他/她收到资金。在这一栏底部的现金净流量是通过将“当天”一栏（要求的投资）的现金流量求和得到的。问号（？）表示如果没有套利利润的时候，投资是否为正、零或者为负。第三栏和第四栏描写了当S_t≥X和S_t<X时的现金流量。所以，未来或许收到零收益（第三栏）或者是正收益（第四栏）。所以问号代表的是正现金流量，在现在或者将来收到资金，这样就得到了非常简单的套利的可能性。当问号为零的时候会出现同样的情况：一个人在当天不用支付，然而却可以在下个时期中得到现金。结论就是在无套利的情况下，问号必须由负数来表示：

表20.5　认购期权的较低界限：现金流量表

资料来源：利维：《投资学入门》第二版。

这暗示着：

得出结论，在方程式20.4中存在着不均等的情况。表20.4（b）代表的是r被认为是5%的较低的界限。注意所有的收盘结算价都在较低的界限之上。例如，91天执行价为45美元的买权报价为6.43，它的较低的界限却是最大值[0，50－45/（1+0.05）^91/365]≈5.54（参见方程20.4）。但是，价格在较低的界限之上的期权的数量是不同的。

用相同的论述，能够示例欧式买入期权的价格一定在较高的界限之下，因此指定股票的价格：

从直觉上来讲，购买证券支付给期权的钱不会高于直接购买指定证券的钱。例如，能够在市场以S_t=$40买到股票，为什么还要支付50美元来购买股票的权利呢？所以，买入期权总是没有沽出期权的指定资产值钱。

图20.6表明的是买入期权的界限。注意，如果拥有美式认购期权并且已经行使，那么价值就是S₀－X。因为c₀>S₀－[X/（1+r）^t]>S₀－X，要在到期之前行使买入期权从来不需要任何支付（投资商更善于卖空期权）。所以，欧式买入期权的界限也可以应用于美式期权。唯一的警告是，当指定资产支付股息的时候，以上的推论并不能应用；这种情况会在第20.4节中加以讨论。

图20.6　认购期权界限

资料来源：利维：《投资学入门》第二版。

20．3．2看跌期权界限

与买入期权类似，欧式看跌期权有价值界限。卖权价格（p₀）的较低界限为：

用来表示买入期权较低界限的交易策略由三个部分组成：

■借入数量$X/（1+r）^t；

■购买1支股票；

■购买一个看跌期权。

表20.7表示的是现金流量。这个表的倒数第二栏在假设S_t≥X情况下为非负。所以，如果当日（0）的现金流量为正（？>0），那么这就是一个套利。即能够在没有未来损失（并且可能是正的未来现金流量）的情况下生成正现金流量。所以，为了避免这个套利，必须找到当日的现金流量为负，这样的结果是：

-p₀+X/（1+r）^t-S₀≤0

意味着：

p₀≥X/（1+r）^t-S₀

如果－p₀+X/（1+r）^t－S₀为正，每个人都想要购买看跌期权，购买股票，借出这台赚钱机器。购买股票和看跌期权会促使股价和卖权价格上升，最后所有的套利盈利都会消失。因为期权的价值是永远都不会为负的，如方程20.6所示。

由于注意到了投资商从卖出看跌期权中的最大损失为敲定价，所以就建立了较高的界限。当股价下跌到零的时候这种情况就会发生。因为这种现金流量是在到期时支付的，并且不是在买入期权购买的当天，所以看跌期权的价格一定是在敲定价的贴现价值之下：

表20.7　看跌期权的较低的界限：现金流量表

资料来源：利维：《投资学入门》第二版。

为什么投资商为期权所支付的要比最大收益的目前价值还要高呢？答案是他们可能不会这样做。例如，敲定价为50美元的无风险利率5%的1年看跌期权拥有较高的界限为$47.62[$50/（1+0.05）^t]。投资商并不会为购买使他们有权利在从现在开始的1年内的最大盈利为50美元的看跌期权多支付47.62美元。唯一的例外就是当天行使的美式期权，对于这些期权来说，较高的界限就是敲定价。

图20.8表示的是欧式看跌期权的界限。此外，价格的有效域仍然是很宽的。为了能够对期权价格作出更精确的判断，必须要进一步观察卖权价值。现在来考察股票、看跌期权和买入期权价格之间的关系。

图20.8　看跌期权界限

资料来源：利维：《投资学入门》第二版。

练习栏

问题以下面的信息为基础，核实General汽车公司的看跌期权和买入期权的收盘价满足的界限条件。到期日为一个月（t=1/12），股价为41.88美元，年无风险利率为3%。是否存在任何的套利机会呢？

解答很清楚，这些价格中没有一个接近较高的界限（买入期权为41.88美元，看跌期权一个月无风险利率的贴现为40美元、45美元以及50美元）。现在考察较低的界限，贴现因素为1/（1+r）^t=1/（1+0.03）^1/12=0.9975，所以，X=$40时，有$40×0.9975=$39.90；当X=$45时，有$45×0.9975=$44.8875；当x=$50时，有$50×0.9975=$49.875。

首先来考虑买入期权。当X=$40时，较低的界限为$41.88－$39.90=$1.98，这个低于3.70美元的收盘价。当X=$45时，注意$44.8875>$41.88，较低的界限为零。当$50时也是这种情况。在两种情况下，较低的界限是有效的。

其次，看跌期权的界限（使用方程式20.6）如下所示：

X=$40 p₀=0

X=$45 p₀=$44.8875-$41.88=$3.0075

X=$50 p₀=$49.875-$41.88=$7.995

可以看到每个较低的界限都在看跌期权价格之下，所以，基于这些观察，并没有套利机会。

20．3．3　期权买卖平价

期权买卖平价（PCP，Put-call Parity）的概念最开始是在19世纪末期由罗素·沙吉（Russell Sage）提出的。期权买卖平价建立了现行股价、在任何指定时刻的结算价以及卖权价之间的精确关系。换句话说，它建立了指定资产、无风险利率、拥有相同的执行价的买入期权和看跌期权之间的关系。只要给出下面四个证券中的任意三种——^[15]指定证券；②零息债券（借入或者借出）；^①③认购期权；④看跌期权——可以合成创造出第四个。也就是说，通过创造三个资产的资产组合，能够复制第四个资产的现金流量。期权买卖平价可以写成如下的形式：

从直觉上来讲，它能够帮助将－X/（1+r）^t转到左手边，这可以显示出买入期权和某个债券与看跌期权和指定资产是等同的。如果画出这两个组合收益图，就可以简单地看到它们的等同之处。另外，还可以假设以时间0开始的交易在到期日（t）结束的期权。表20.9解释了方程20.8的有效性。

像以前一样，表20.9的第一栏确定了在日期0当天采用的交易策略，其他的三个显示了相关的现金流量。净现金流量只不过是来自于投资的所有现金流量的总和，因为未来的现金流量都是零，所以当天的价值也应该是零（不考虑使用的贴现率）。重新安排术语就会得到方程20.8。期权买卖平价的任何偏离将会导致套利机会，就像在这一章的说明部分所说的那样：那个例子中的价格违背了期权买卖平价。

表20.9　期权买卖平价：现金流量表

资料来源：利维：《投资学入门》第二版。

人们也可以调整用于支付股息的股票的公式；稍后我们将使用这个公式。假设股息率是固定的百分数（所以股息取决于支付时的股票价值），那么期权买卖平价就可以通过以下的公式表示：

练习栏

问题使用General汽车公司问题中的信息，评估当执行价为40美元时期权买卖平价是否有效。

解答从方程20.8得到：

c₀为3.70美元，p₀为1.75美元，S₀为41.88美元，X为40美元，r为3%，t为1/₁₂。需要评估下面的等式是否存在：

所以，期权买卖平价并不精确有效，但是，由于交易成本，要从这种分歧中盈利也是不太可能的。实际中，期权买卖平价是非常紧密的。

20．4　二项式模型

在这一节，我们来讨论以给出期权而不是界限条件定价为目的的两个模型。有两个模型的原因是：在以前的章节中已经看到，投资可以用分散的利率和连续的复利来定价。这个区别——以及选择的数学上的结果——就导致了关于衍生工具尤其是期权定价的两个方法：分散时间（Discrete Time）模型和连续时间（Continuous Time）模型。第一个叫做二项式模型，它假定价格只会在事先预定的事件发生变化并且在期间保持稳定；后者（布莱克—斯科尔斯模型）假定价格连续地改变——并不是在每一秒而是一直在变化。这些方法在结果中是等同的（如果是相同的假设，连续时间方法经常要求一些另外的假设来得到结果），但是它们在不同情况中的使用却有着不同的优点。在这一节，首先将使用分散时间方法在期权定价中得到一些基本的结果；在下一节，转到连续时间公式，并且进行详细地讨论。但是，之前必须要处理界限和定价模型之间的关系，这个关系涉及时间价值（Time Value）。

20．4．1　时间价值

期权价格在界限中的什么地方呢？答案可以由时间价值来提供。衍生价格可以分成两个组成部分：内在价值和时间价值。如在第19章中看到的，衍生工具的内在价值是这样的一个价值：如果期权立即行使，并且股票由收购它的一方卖出。即使期权是价外的，股票价格或许会改变以及期权或许会以价内结束的可能使期权具有时间值。^[16]用c₀和p₀分别代表买入溢价和看跌溢价。那么认购期权的时间价值（TV_c）为：

看跌期权的时间价值（TV_p）为：

期权变为价内的可能（或者如果已经在价内的话就保持在价内）和可能的大小决定了期权的时间价值。不精确地说，可以确定如下的因素（将在第20.5节中连续时间的条件下更加精确地介绍这个内容）会影响可能性和价值：

■指定资产价格变化的数量：如果股票的价值有规律地变化，那么价格移动到期权在价内的区域的可能性要比股价几乎不移动的时候大。

■未来支付的贴现率：任何的现金流量（包括到期时来自于价内期权的那些现金流量）都有比名目金额低的当前价值。如果想知道当天的期权价格，知道低多少是很重要的。

■期权到期之前剩余的时间：这会影响到贴现和估价会在有利的区域内结束的可能性。

这些因素的相关重要性主要取决于现行股票价格和执行价之间的比率。

练习栏

问题假设下面给出的是TotalFinaElf公司的期权报价：

计算每个期权的内在价值和时间价值。

解答内在价值是价内期权的美元数量。对于买入期权来说，140美元敲定价中只有4美元是在价内。对于看跌期权来说，155美元执行价是价内1美元，160美元是价内6美元。所以，构建内在价值的表如下：

aIV_c=最大（0，S₀-X）=最大（0，$154-$150）=$4

bIV_p=最大（0，X-S₀）=最大（0，$160-$154）=$6

时间价值只是用期权价值减去内在价值，构建时间价值的表如下：

aTV_c=c₀-IV_c=$7.50-$4=$3.50

bTV_p=p₀-IV_p=$7.75-$6=$1.75

20．4．2　二项式期权定价模型

期权界限在解释期权价格方面是有用的，但是它们过于宽泛；所以定价期权需要更精确的办法。二项式期权定价模型［或者简称二项式模型（Binominal Model）］是期权定价研究的相对简单的方法。称为“二项式”是因为，就像统计学中的二项式分配一样，如果给出时期开始的价值，它假设在一段时期的结束只有两个未来的股价（结果）是可能的。这是在分散时间情况下期权定价的主要工具。类似于所有的定价模型，二项式模型是基于以下的几个假设：

■资本市场要以完全竞争为特点；

■允许使用所有的利率卖空；

■投资商偏爱更多的财富；

■允许无风险的借入和借出；

■未来股价将会是两个可能价值中的一个。

第一个假设与在第11章中说明套利定价理论（APT）时的假设是一样的。对于期权定价，最重要的元素是无摩擦市场（Frictionless Market）（这是没有成本交易的市场：没有税收、买卖价差、经纪手续费等），并且假设投资商都是价格接受者（也就是说没有一个单独的投资商可以很大地影响价格）。如在第3章中讨论的，卖空是在一个人不拥有在未来将股票还给借贷人的理解的时候卖出股票。注意第三个假设并不暗示着风险态度：投资商也许是风险厌恶的、风险中立的甚至是追求风险的。构建对冲资产组合需要第四个和第五个假设。

买入期权的二项式模型用五个步骤说明。

第一步：确定股价分配

假设股价可以从现行水平S₀只变化到两个可能的未来价值中的一个，S_u或者S_d，其中u暗示着股票上升，d为股票下跌。为了在现行价值方面表达未来的股票价值，设定S_u=uS₀和S_d=dS₀，其中u和d是恒量，d<1+r<u。^[17]用图表示得到：

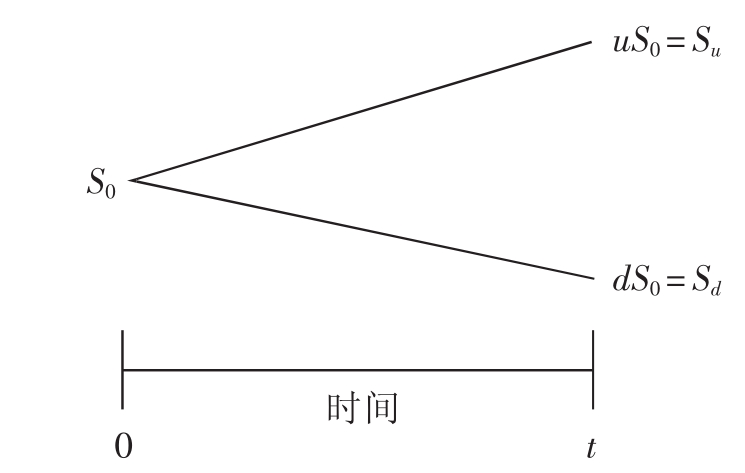
例如，假定有如下的信息：S₀=$100，X=$100，u=1.10，d=0.95，r=0.05。有了这些数据，S_u=$110，S_d=$95。该模型假定其他股票价格已知，在到期日，股票价格为$110或$95。但是，就像在以后的讨论中要看到的，在这种情况下能够不用知道S_u或S_d将要出现的可能性就可以确定期权的平衡价值。

第二步：确定价格分配

知道了第一步，现在就能够计算到期时的买入期权的价值。特别地，到期的期权价值如果是在价内的话就只是美元的数量，也就是说，能够用如下方式描述结算价分配：

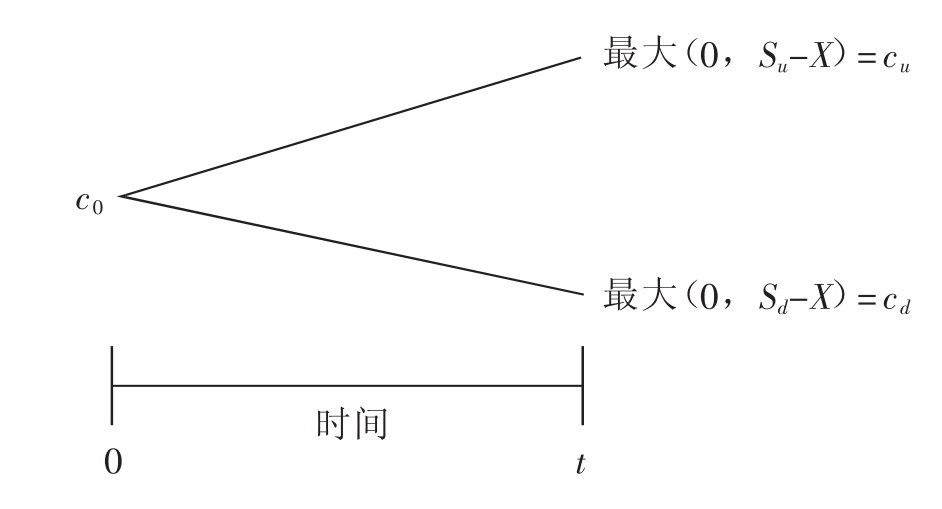
例子中的数据引起了如下情况：在u情况下，价值是0和（110－100）的最大值，也就是10美元。在d情况下，价值是0和（95－100）的最大值，也就是0。

第三步：创造对冲的资产组合

在这一步里，构建买入期权和涉及股票的动态期权对冲的资产组合。但是，仍然不能确定在资产组合中两支资产的比例。在第四步中，对这个资产组合做何改变提供已经确定知道的现金流量，所以就有了“对冲资产组合”这个词。通过构建对冲资产组合可以满足目标。考虑如下的策略以及在表20.10中描述的合成现金流量。

对冲的资产组合是由第一次售出（即沽出）买入期权建立起来的。这个行为引起了当天期权价格的正现金流量（+c₀），但是它要求支付到期时的期权价值（如果有的话）（－c_u或－c_d）（见表20.10）。接下来，不具体的股票的份数（h_c）被购买—数量h_c将在第四步中明确。出售股份的收益将为h_cS_u或者h_cS_d。那么通过在这一交易策略中添加组成部分的现金流量就建立了净现金流量。

第四步：解决h_c

必须卖出买入期权的股份的数量由h_c来表示。在第四步开始的时候，有当天0的净现金流量，到期日则取决于两个未知的变量——在0的结算价（c₀）以及h_c，叫做对冲比率（Hedge Ratio）。之所以叫做比率，是因为我们正在寻找为了消除未来的风险而沽出的每个买入期权所要买入的股份的数目。也就是说，发现沽出的买入期权和购买的股票之间的比率能使未来的现金流量变得确定。为了这样做，当S_u出现的时候，采用对冲资产组合的净现金流量，并且设定其与S_d出现时的净现金流量相等：

表20.10　一个时期的二项式模型对冲资产组合定价认购期权

资料来源：利维：《投资学入门》第二版。

-c_u+h_cS_u=-c_d+h_cS_d

在这种情况下，不考虑股价上升或下跌，资产组合的现金流量是确定的。因为所有的价值都与h_c分开，解决h_c：

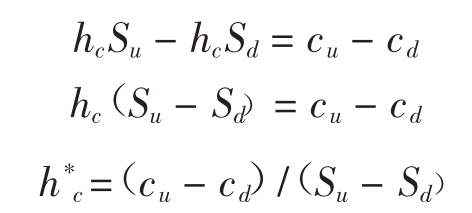
其中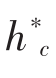代表选择的对冲比率，将uS₀用S_u替换，dS₀用S_d替换，得到：

所以，对冲比率可以用知道的数据时间t=0来计算。使用例子中的数据，得到：

为了创造对冲资产组合，我们售出了购买的每支股票份额的2/3。作为选择，对于购买的每2份股份，会售出3个买入期权。实际上，由于合约有100份股票作为指定资产，对于每200份购买的股票，要购买3个认购期权合约。

练习栏

使用h^*_c=2/3，可以创造无风险的资产组合。这个练习表明了当h=1/2的时候（即，不同于2/3的价值），会产生有风险的资产组合。

问题证明当h=1/2的时候，得到的是有风险的资产组合。

解答1/2的对冲比率暗示着对于每一个沽出的买入期权，需要购买股票的1/2股份，能够构建结果的表格如下：

有了这个资产组合，未来的结果是不确定的（或者是45美元或者是47.50美元）；所以，这个资产组合是有风险的。只有h^*_c=2/3的对冲比率可以创造确定的现金流量，并且只有这个对冲比率适合套利策略和期权定价。

第五步：使用净现值解决买入期权的定价

现在有一个标准的净现值（NPV）问题。如果选择了h^*_c作为购买了股票的份数，那么未来的现金流量是确定的，改变贴现率的问题也就在资产组合的水平上消失了。由于未来现金流量已经确定知道了，适合的贴现率就是无风险利率（r）。

标准的一段时期的NPV问题如下面所写：

其中CF₁是时段1的现金流量，r是贴现率，I是要求的被用作负数的投资。在平衡状态下，净现值一定是0。如果NPV＞0，所有的投资商将会购买这样的资产组合，使得它的价格上升。如果NPV＜0，所有的投资商都会出售资产组合，使得它的价格下降。事实上，价格很少大幅度偏离NPV=0。

在例子中（见表20.10），到期日的现金流量为：

和：

将这些结果代入方程20.12结果如下：

$63.33/（1+0.05）=$66.67-c₀

解决c₀，有：

买入期权的二项式期权定价模型的一般表达式为：

看跌期权也可以用这种方法简单地定价；下面的练习让我们去确定看跌期权的公式。也可以使用期权买卖平价。在平衡状态下，例子中的买入期权价值为6.36美元。如果结算价是其他的价值，那么无风险的生成无限利润的机会将会存在（如果买入期权价值为6美元或7美元，证明怎样可以生成无限的利润）。所以，在例子中平衡的结算价为6.36美元。

需要指出的一点是，我们没有提及与股价上升或下跌相联系的可能性，所以，可以正确的推断出在当天S₀对于给定的股价，期权价格是独立于未来期待的股价的。这个令人困惑的结果可以得到如下的解释：尽管可能性并不直接影响c₀，而是间接地影响。例如，如果提高了S_u的可能性，就升高了S₀（否则就会再次制造一个套利机会——简而言之，会发生这样的情况是因为对于（贴现）未来股价的最好的估计就是现行价格），并且S₀的增加会增加c₀的价值。

更重要的问题是要怎样确定u和d——这些变量确实影响h^*_c，c_d和S_d。事实上，它们决定的是时间价值，因为暗中给了期权会在价内以及考虑到期日的可能的价值。为了得到最好的结果，应该选择u和d来搭配股价运动的特点。一种流行的（但是不是唯一的）方法就是通过观察收益率分配的波幅进行设定：

其中σ是收益率的标准偏差，t是到期的时间（两个都应该用相同的时间比例来测量，因为将每天的标准偏差与以年测量的时间联合起来是没有意义的）。在这个选择背后的想法和数学在这本书的范畴之外，但是感兴趣的读者应该参考一下这一章最后给出的参考文献。^[18]

练习栏

也可以在看跌期权方面使用二项式模型。

问题定价股票的欧式期权S₀=$100，X=$100，u=1.10，d=0.95，r=5%。

解答像以往一样，创造看跌期权的资产组合，以及未来现金流量确定的指定股票。首先确定对冲比率为1/3（将未来现金流量视为相等），那么解决p₀。所以，就像表20.10一样，确定看跌期权的价值。

认沽期权的对冲利率为：

在例子中，

现金流量如下所示：

所有的都是正常的记号。因为$36.67/（1+0.05）=$34.92，等于－（－p₀－$33.33），买入期权的价格p₀则为$34.92-$33.33=$1.59。

将结果扩展到多个时期

没有理由要把二项式模型的应用限制在一个单独的时期内：简单地在第一个时期之外插入第二个时期（或者把现在的时期分为两个），这样就会引起下面的二项式树形图（Binominal Tree）：

有了这一时期最开始的价格，在第二个时期结束的时候也有两个可能的股价。在第二个时期之后，我们看到这些可能（第一时期中下跌之后的上升，以及第一时期中上升之后的下跌）的两个，最后产生了相同的结果：树形图被称为是重组（Recombinant）的，并且它是由于在每个时期乘以u和d引起的。这是这个二项式树形图的一个便利（但不是必要的）属性。另外一个引起注意的是在树形图中，似乎在两个时期之后，有两个阶段中的指定资产的价格是在它的原始价格之后的。尽管差别通常是小的，但是不能够从总体上说S_ud=S₀。但是如果使用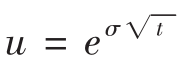和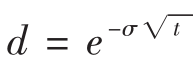，或者其他任何的包括d和u互为相反的设置，考虑无股息支付的股票，任何包括同等数量的上升和下跌的状态都会有价格S=S₀。

树形图解决c₀的方法是相似的，但是必须从最后一个时期开始。为每个结果在时间t₂确定期权的价值。那么为上一个时期中每一个结果设定确定对冲比率。所以在例子中，一旦从S_d和S_u开始，就计算上个时期的两个h。从这一点看，计算时间t₁的期权价值：S_u的价值（由c_1u表示）和S_d的价值（由c_1d表示）。所以，在方程式20.11中的S₀应该由S_u或者S_d来代替，方程式20.13中的S₀和S_d也应该相应地做出调整。那么我们就用以上描述的方式使用c_1u和c_1d（计算第三个h）来计算c₀，这就是答案了。注意所有的对冲利率（h）是不同的，反映了对冲资产组合动态的本质。

以相似的方式，可以将到期的时间分为更多的时期，这样会产生更好的可能结果。这是值得做的，因为在一个时期情况下，假设指定资产在到期时只能有两个价值。如果使用几个次时期，就可以允许更多的可能性，就会得到更近似的答案。但是，随着次时期数目的增加，计算的负担也会急剧地增加。因为，从业者会使用计算机来处理几十个，就算不是成千上万个次时期。在这本书末尾的附表B中，给出了包括50个次时期的应用。强烈建议读者研究一下这个电子数据表。

20．4．3　其他期权的二项式模型

二项式模型可以应用到欧式的买入和看跌期权之外的期权。因为期权的价值可以在任何时间计算（通过选择适当数目的次时期），二项式模型的灵活性可以用来为拥有依赖期权有效期内发展的价值的期权定价。讨论两个例子：美式期权和喊价期权，后者为第19章描述的外来期权。

美式期权的早期行使

美式期权可以从它们早期行使的可能性中获得价值。二项式树形图的方法是能够比较行使时的价值和不行使时的任何一点的期权价值。有两种情况，其美式期权的价值比欧式期权大：

■股息在买入期权的有效期期间支付。回忆第15章中的在股息支付之后，股票的内在价值会立即下降。行使价不会被这个纠正。^[19]如果股息足够大，有可能价内买入期权会在一夜之间变为价外买入期权，贬低了期权的价值。如果再付息日之前的买入期权的内在价值高于股息支付后的总价值，那么就会发生早期行使。在二项式树形图中，人们必须要纠正在股票付息时的所有股份的价格。最方便的方法就是确保付息日在一个次时期的末尾。那时，直到付息日，计算价格（从后面开始）；然后把股息与股份价格相加，重新计算付息日的价值。

■如果在处于金融困境的公司购买看跌期权，它的股价为，比如说，1美分。如果执行价为10美元，那就最好行使早期行使的权利，得到现金流量（少于1美分），将资金存到银行赚得现金流量的利息。收到的利息或许会大于将期权持有到期日得到的最大的额外利润（如果股价降到零最大值为1美分）。并不需要为此改变二项式树形图，只要在每一点及时的计算内在价值并将其乘以（1+r）^t。如果这个值大于期权的价值，那么就确保了早期行使。

因此，可以看到美式期权可能具有比欧式期权高的价值。对于买入期权来说，只有当指定资产支付充足的股息的时候，才会出现不同。对于看跌期权来说，只有指定资产变得一文不值的可能性增加，区别才会变得更大。

喊价期权

二项式模型对于具有早期行使的可能性，改变其执行价，取决于期权有效期内的指定资产价格的期权价值，以及外来期权的定价。如果由于这些变量在收益中有变化，那么这个变化可以在以后的时期中考虑进来。

一个相对简单的例子就是喊价期权。如在第19章中提到的，喊价期权的收益与正常期权的收益是相等的。也就是说，除非买者在过去决定喊的内在价值并不高（本质上讲是使这个期权合约的最小收益为它的价值），在这样的情况下，这个价值就由买方收到。如果用S*代表在喊价期权时间的指定资产的价格，那么到期时的收益为：

最大（0，S_t-S*）+（S*-X）

是否对某支股票的价格喊价决定取决于期权的价值，但是这个价值反过来又受到喊价决定的影响。二项式模型可以解决这个问题：如果在节点喊价或者不喊价，就要计算每个节点的价值。那个节点的期权的价值是两个中较大的。另外的复杂性在于只能喊价一次——之后，即使接下来会有更大的盈利，但是却没有再次喊价的机会了。所以期权的价值取决于较早采取的行为，但是必须从末尾开始解决二项式模型。如果假设投资商是在他/她有最大赢利的时刻喊价的，必须要计算所有可以喊价的时刻的价值，然后选出最具有营利性的。^[20]将在最简单的可能情况下简短地说明这一点：两个时期的二项式模型。另外，任何实际的应用都需要更多的时期，在那样的情况下计算机在计算方面就显得尤为重要了。

假设u=1.1，d=0.9，无风险利率为5.0%，S₀为100美元。使用二项式模式，可以计算执行价为95美元的买入期权的价值。期权具有如下的结构（在节点上方代表价值S的数字，在节点下方代表内在值c的数字）。

有了这些假设，如果投资商从不喊价的话，就可以及时计算每个节点的期权的价值：

现在，来研究这样的情况：如果投资商在不同的时刻喊价。首先，在时间t₂喊价是没有意义的，因为投资商无论如何都会得到那一点的内在价值。如果投资商在时间t₁喊价，那么t₂的最小收益就会是内在价值（0或者15）。如果在第一个时期内有价格的上升，那么也就意味着在t₂收益为26或者15。如果有S_d，其值为4或者0（因为在S_d没有内在值）。现在假设在t₁喊价通过替代收益计算期权的价值：它们变成了26，15，4和0。注意资产先上升后下降的收益与S_du是不同的。使用这个，可以看到如果投资商在t₁喊价，那么t₀的价值就是16.50美元。这个要多于14.62美元，所以投资商t₁喊价要好于他/她永远不喊价。

现在看一下这样的情况：如果投资在t₀喊价。在那个时刻的内在价值是5美元。在t₂的收益会分别变成26，5和5。t₀的价值为15.25美元，要少于在t₁喊价的值。所以，如果股价上升的话，投资商最好在t₁喊价（在第一时期如果股票价格下降投资商是否要在t₁喊价与这种情况并不相关）。有了这些参数，模型不明显地假设了股价上升很高的可能性，所以在这个例子中，值得我们怀着能够在t₁封锁大的内在价值而不是立即封锁5美元的内在价值的希望等待。所以，尽管只是一个估计，如果时期的数目是有限的，那么如果期权价格表现出外部特点的话，二项式模型是非常方便的。

20．5　布莱克—斯科尔斯期权定价模型

布莱克—斯科尔斯期权定价模型（BS模型，Black-Scholes Option-Valuation）是在1973年由布莱克和斯科尔斯确立的。默顿几乎是在同时开发了默顿模型（Merton Model），已经证明它拓宽了BS模型的视野。这些模型与在20世纪60年代和70年代提出的模型是不同的，因为期权价格并不取决于指定股票的期待的收益率这个在实践中不可观察的变量。^[21]另外，模型是在完全对冲的没有风险的期权创造基础之上的。所以无风险利率就被用来贴现未来现金流量，遵循价格无套利的基本原则。

为了更好地理解BS模型的用处和局限，来研究一下BS模型要求的基本假设：

■资本市场以完全竞争为特点；

■允许使用所有的利益进行卖空；

■投资商偏爱更多的财富；

■以无风险利率借入和借出；

■价格运动为这样的情况：过去的价格运动不能用来预告将来的价格变化；连续合成的收益率是正态分布的。

前三个假设与在20.4.2节中提到的二项式期权价值模型的假设是一样的。另外，最重要的元素是无摩擦的市场以及假设投资商是价格接受者。

以无风险利率借入和借出的假设与标准实践保持一致。它是连续合成的假设是为了方便而设定的，也是为了把这个模型放到连续时间的框架之中，这与二项式模型的分散方法相反。没有必要在BS模型中使用过多的次时期来得到近似值：如果假设是真实的，进入项是正确的，那么结果就是期权的精确价值（当然真正的问题是：这些假设是真实的吗？如果它们不正确，影响是什么？有正确的进入项参数吗？这些问题将在下一节解决）。第五个假设确定了股价的分配。未来收益率不能从过去的收益率中得到预示的假设是布莱克和斯科尔斯在创造BS模型的时候使用的。但是他们又更近了一步：假设连续合成的收益率是正态分布的。结果是，收益率具有了一个可能的分布状态，那就是统计学中的对数正态分布（Log-normal Distribution）。^[22]

尽管随着时间变化而对股价运动所作的假设的不同，BS模型与二项式模型有着直觉的联系。如果把从0到t的时期分成几乎无限数目的次时期，并且允许在每个次时期内股价以很小的数量上升或者下降，那么合成的期权价格接近于BS模型的价格，有限来讲（次时期的数目为无限大），它们产生了相同的结果。

20．5．1　公式

布莱克、斯科尔斯和默顿使用了以上列出的假设和在二项式期权定价模型中的相同无套利观点，开发了定价买入期权的公式。^[23]乍看起来，BS模型是十分复杂的。但是，当渐渐熟悉了符号以及系统解决期权定价问题的步骤之后，许多问题都消失了。另外，微软包和电子数据表（例如，本书末尾附录B中的内容）使得BS模型的使用更加简单了。

买入期权的BS模型如下所示：^[24]

其中：

方程式20.14，20.15，20.16的其他参数如下所示：ln（·）中的是自然对数，σ是连续合成的、股票收益率的年标准偏差，r是连续合成的年无风险利率，t是一年的分数形式的到期的时间（在附录B中的电子数据表中，需要加入t作为到期的天数），X是执行价，S是现行股价，e是自然对数的底，约等于2.71828。所以需要6个变量（σ，r，q，t，X和S）使用BS模型来计算认购期权的价格。

使用微软的软件，如在附录B中提到的Excel程序来计算BS买入期权价格是很简单的。B.7部分给出了很多不错的例子，强烈建议读者阅读。在这些程序要做的就是输入S，X，σ，r，q，t和c出现在屏幕上。但是如果进行一下练习，人工计算也不难；只需要知道如何运用标准正态分布的表格来计算N（d₁）和N（d₂）。

看跌期权

看跌期权的合适的公式可以在BS模型中买入期权以及期权买卖平价中找到。重新安排方程式20.8（使用连续合成而不是分散合成）就会得到下面的结果：

所以，可以通过把买入期权定价方程式代入方程式20.17来给看跌期权定价：

p=Se^-qtN（d₁）-Xe^-rtN（d₂）-Se^-qt+Xe^-rt

重新安排各项，发现：

p=Xe^-rt[1-N（d₂）]-Se^-qt[1-N（d₁）]

也可以用下面的方式表达：^[26]

20．5．2　不同的输入参数

现在要来处理输入参数变化的影响：期权价格是不是因为上升的利率大幅度的变化呢，或者因为上升的波幅？或者是下跌的利率？这些问题的答案在理论上和实践中都是重要的。在这一节，将考察，如果输入参数变化（或是错误估计），期权价格会发生什么样的变化。为了参考简单，表20.9定性地给出了结论。

Delta

以股份价格开始，可以得到买入期权的价格变化方向与S.莫尔（S.More）特别提出的是一样的，这个变量叫做Delta（Δ），表示如下：

这意味着如果股份价格上升1美元，那么认购期权将会上升Δ美元。^[27]对于输入，Δ= e^－qt[N（d₁）－1]。买入期权总是为正，看跌期权总是为负。警告：用Δ计算的价格变化只是（线性）近似。在图20.12的细线代表了这种近似。股份价格的变化越大，近似就变得越不精确。

Δ与在二项式模型中遇到的对冲比率是相等的。对于任何的股份价格，复制的（套利）资产组合包括Δ股份和一个空仓。如果总资产组合（即期权和股份）的价值并不随着S的改变而改变，那么就叫做Δ中立。期权中的动态对冲都以Δ对冲开始，即利用Δ股份来得到第一个近似值。这个方法的危险在于股价的大规模改变；如在图20.12中看到的，S的翻番使得投资商很糟糕地被对冲。

表20.11　输入参数上升时期权价格的反应

图20.12　对冲冲突

Gamma

以上所说使得拥有动态对冲的投资商也要考虑买入期权指定资产价格变化影响的另一种方法。这就是Gamma（Γ）；其与Δ一起可以形成图20.12中的价格弧线的二次近似。这可以客观地减少误差。技术上来讲，Γ是期权价格变化和股价的平方变化的比率。^[28]这个公式对于买入期权和看跌期权是一样的：

其中，e是欧拉数（自然对数的底，2.71828），π是π值（3.14159），d₁，S₀，σ和t和以前定义的一样。e和π的进入是由于BS模型所作的关于收益率的分布。

当形成二次近似的时候，是以如下的方式进行的。在过去的结算价c₀的基础上，在S（从S₀到S）改变之后的新价格是：

Vega

另一个重要的输入参数是标准偏差。随着标准偏差的变化，结算价变化的比率叫做Vega（V）。如果波幅增长了1%（假设是以每年的百分数测量），或者是分数0.01，那么结算价增长0.01V美元。注意V总是为正；期权是不对称的工具，下方比上方的潜力大。上升的波幅增加了期权变为价内以及升高价值的可能性（即使期权已经深入价内了）。

其公式为：

与其他的灵敏度相比，这个价值经常是高的。于是估计正确的标准偏差（下面将要讨论）就很重要了。V可以被视为当标准偏差被轻微错误估计时所犯的错误：假设已经估计标准偏差为0.24，但是关心的是标准偏差可能是0.26。在这两个估计基础之上的期权价值的不同可以表示为0.02V美元。

Rho

利率变化的期权价格的灵敏度叫做Rho（ρ）。其与买入期权和看跌期权是不同的。对于买入期权来说，可以表示为：

在看跌期权的情况下，变成：

ρ=-tXe^-rtN（-d₂）

注意这个公式假设利率以分数的形式写出，所以一个基本点是0.0001，无风险利率增长25个基本点引起了买入价格0.0025 ρ美元的上升。还要注意的是方程式并不把ρ作为论据；公式与股息支付和非股息支付的指定资产是一样的。

衰减时间

即使没有输入参数的改变，时间价值仍将会变化，仅仅是由于时间的变化。这并没有它听起来的那么奇怪：假设有一个人下了赌注，自己喜欢的（但是最后的结果却是灾难性的）足球队至少在接连的5场比赛中将会胜出。在球队已经输掉了5场比赛中的4场的时候，这个人是否还应该继续赌注用相同的收益以及同样的比赛？与这个赌注相似的，期权是受衰减时间（Time Decay）影响的：如果不增加内在价值，那么收益的部分可能会在这段时间内消失，对价值的其他部分也是这样。

其他方面

在讨论了Delta，Gamma，Vega和Rho之后，人们或许会问：6个输入参数就是所有了吗，我们只给了3个公式类型的灵敏度（与S，σ和r有关系）？^[29]确实可以确定与利率相像的股息率的灵敏度，也可以计算衰减时间期权价值的灵敏度的公式（尽管是一个很长的表达式），通常称为theta（θ）。最后，估计X的灵敏度是没有多大意义的，因为它是设定在期权合约中的，并且不能为了正常期权改变。

所以从理论上来说，如果单独的输入参数改变，就能够从（近似）价格变化中得到。从业者也经常察看两个输入参数的比率，也就是S/X，叫做货币性（Moneyness）。^[30]这个词是用来描述期权是否是在价内还是价外的。期权的货币性意味着期权是等价的。图20.13a－b显示了买入和看跌价格变化的货币性的影响，以及衰减时间和波幅对买入和看跌价格的影响。

注意在到期日，结算价是0或者S－X。但是，在到期日之前，BS模型显示的是在较高界限和较低界限之间的弧线的结算价。很清楚，结算价是与货币性正相关的。图20.13a－b还表明了之前讨论过（参见方程式20.4－20.7）的界限情况。图表明当股价以较大的数量上升或者下降的时候，期权聚集到较低的界限。

注意图20.13d中期权价格对波幅的估计（很难获得）是很敏感的。例如，在原始估计S=X=$100，r=5%，t=1，σ=30%的基础之上，BS模型的结算价是13.58美元，看跌价格是8.70美元。如果之后确定波幅实际上是σ=25%，那么BS模型的结算价则为11.72美元，看跌价为6.85美元。期权价格极限为16%（（$13.58-$11.72）/$11.72）和27%（（$8.70-$6.85）/$6.85）。所以，在试图定价期权之前拥有对波幅的正确估计是很关键的。

20．5．3　估计BS模型的输入

在BS模型中有6个输入参数：σ，r，q，t，X和S。现行的股价（S）是可以通过阅读金融媒体例如《华尔街日报》和《金融时报》简单地获得的。也可以通知经纪人或者订购信息服务，例如，路透社网站（Reuters）或者财经新闻集团的Bloomberg。最后但不是最不重要的，也可以在互联网上免费的找到，但是通常都有较短时间的耽搁。执行价（X）在期货合约中较具体，并且发表在金融媒体中。

到期日（t）是直到期权的所剩年的分数，对于年份是否应该在交易日（市场开市的日子，大约是1年250天）来测量或者是历日（365或者366天）来测量还是有些争议的。对于利率的计算，历日的使用是相关的。但是当用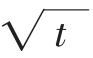和标准偏差相乘的时候，到期日也影响期权变为价内的可能性。对于交易日波幅的测量（所以，t保持一致性）存在争论。但是，用历日测量t却是达成共识的。因此，如果在到期日之前有73个历日，那么t=73/ 365=0.20，假设这一年不是润年。

图20.13　在指定参数中期权价格对于变化的灵敏度

资料来源：利维：《投资学入门》第二版。

无风险利率（r）的估计也是比较困难的。应该使用无违约的定息证券，例如，美国短期债券。所以，使用的合适利率是到期最接近期权到期日的连续合成受益。例如，如果期权是1年的t=1/5，那么需要现在以P_B交易（债券的价格）1年的1/5支付1美元的短期债券。数学上，有以下的关系：

P_B=1e^-r1/5=e^-r/5

或者

解决r_c：

所以，用观察到的价格P_B，能够解决r。第6章详细讲了分散和连续利率之间的关系。回顾那一章，美国短期债券在贴现基础上1年360天的报价。也就是说，价格并没有广泛地报告。在报告的贴现率的基础上计算连续复利要求使用下面的公式：

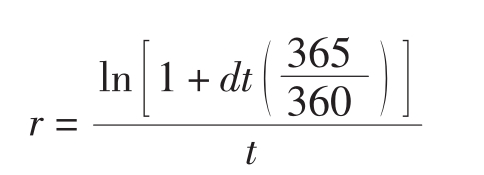
其中d是债权（买卖比率之间的平均数）报价的贴现率，t是年的分数，ln[·]是自然对数函数。

红利率q是在期权的有效期内支付的股票的年百分比股息。另外，百分比是使用连续合成计算的。^[31]但是，默顿模型也可以应用于其他指定资产的衍生工具，比如说，外国货币。在那样的情况下，q不是股息率而是外汇率。在商品期权情况下，q可以被用于代表持有资本的成本。它们每一个应用都要求具体的估计过程，所以在这里就不讨论了。

最后一个也是最难估计的参数是股票收益率的波幅，由σ来测量。有几种方式来测量波幅，包括使用历史收益率数据。以前讲过，收益率的标准偏差样本是在下面的方程式的基础上：

其中R_t是在时间t内的连续合成的收益率，R是指定红利的平均收益率，n是历史观察的数目。第6章提供了分散时间的收益率。当用连续合成计算标准偏差的时候，需要做的唯一的调整就是计算R_t的方程式，变成为：

其中ln[·]是自然对数，D是股息（美元）。

可以显示在足够短的时期内（或者股价的小变化），任何一种合成方法的收益率大概都是相同的。但是，对于长期持有时期（长于一个星期），区别就更大了。

然而，这并不是故事的结局：最困难的问题是在方程式20.25中选择n和t。股票市场波幅在一段时间内并不是常量，所以如果使用了过去5年的来计算σ，很有可能得到与一个月的答案的不同。^[32]两个主要的问题是波动性峰值（Volatility Peaks）和均值修正（Mean Reversion），接下来会讨论。注意这些并不是BS模型特有的问题。在二项式模型中，还需要预计波动性来确定u和d。

波动性峰值

如果确定了使用的时期来计算，波动性峰值就很有问题了。这个可以得到最好的说明，通过考虑在这个固定的时期内出现的市场崩溃。随着时间的流逝，市场崩溃出现在了固定时期之外，波动性的估计变得更低了。例如，如果使用过去一年来估计波动性，那么预计在2002年9月10日会很高，而在2002年9月20日就会低得多，仅仅是因为如果提到去年，具有例外变化的少数的几天（2001年9月11日和之后的日子）并不包括在内。^[33]当然，变化竟然大幅度的下降仅仅是因为主要的事件突然在预计时期之外也是不现实的。2002年9月10日的变化不太可能与2002年9月12日的相同。这并不是个新问题（例如，1987年市场崩溃），很多解决方法可以使用。最简单的方法是使用指数加权移动均值（EWMA，Exponentially Weighted Moving Average）。方法为：不是给每个观察相等的权数也不是把自己限制在某一个时期内，考虑所有的数据，但是数据的权数随着它们远近程度而递减。所以是最近可以得到的数据的重要行为，假如说，w（满足w<1），之前的为w²，等等。经常使用的价值w在0.8和0.99之间。

考虑股票指数变化的一系列的周观察，w为0.9。如果这一周有一个大的变化（如0.2而不是0.01）出现在10周之前，那么这个观察的权数仅是现在时期的0.9¹⁰=0.349倍。这意味着平均价值的20倍的观察仍然具有巨大影响，这是值得的。但是在26周之后，比率为0.065，在一年之后为0.004。所以，极端观察的影响逐渐下降，防止了变化估计中的大的跳跃。

均值修正

均值修正是用来描述如下的情况：不考虑偶尔的（或者稍微长一点的）偏差，一定的参数在长期内回到固定的均值；变化倾向于表示这一类型的行为。指数加权移动均值模型并不适合实践的事实，因为最近的过去得到最大的重要性。所以，如果在过去的时期内的变化在平均值之上，下一个时期的估计也会这样。然而由于均值修正，这个预计很有可能会很高。有时这关系到期权定价领域，甚至更高级的方法，例如，广义自回归条件异方差模型（GARCH），可以提供要求的灵活性。但是，计算和理论的复杂性也使得只有较大的投资商和研究者可以有规律的用这些类型的模型进行工作。

理论联系实际20.1

FT

不稳定力量的多变本质

不稳定性是金融市场中普遍力量。在2000年4月14日，道·琼斯出现了10202低点和10923高点，在6个半小时的一个交易时期内上下波动700点（7%）。这个区域大约是每天1.5%区域的5倍。当指数基金的投资商看到投资的价值在1天内在7%的范围内波动，就已经面临着令人担忧的前景了。

这样的事件是否不同寻常或者我们能不能在未来看到更多这样的情况呢？……

预报

要预报波幅，知道更多的关于一段时期内波幅变化是很重要的。例如，是否与过去的波幅相连？在市场下跌的时候是否会上升？很多实证研究已经使用了创新的统计方法……

由风险测量专家风险衡量使用的简单方法是“指数平滑”法。它使用指数衰减权数，越接近现在的资料的权数越比早期的大。这个方法使用的是即时查询全书，并不考虑以上提到的大多数现象，例如，均值回复或者是波幅和价格变化之间的负关系。

方差研究一类的模型，是由专家罗伯特·恩格尔（Robert Engle）发起，由蒂姆·博勒斯夫（Tim Bollerslev）、丹尼尔·尼尔森（Daniel Nelson）和其他人推广的，它是以波幅在一段时期内不同以及保持稳定为基础的……与风险衡量模型不同，它可以说明波动性在一段时间内回到均值……

引申波幅

尽管这些模型试图包括所有能得到的统计信息，但是他们不能使用来自于期权市场的信息。期权价格是由波幅决定的，在其他因素中，能够使用期权的价格来减少由这个价格引申的波幅。换句话说，期权的价格反映了市场参与者对指定资产未来波幅的感觉。因为期权市场的引进，引申波幅广泛地应用。尽管它是来自于布莱克—斯科尔斯期权定价模型，并且依赖于那个模型的假设，但是却可以有不同的应用，包括波幅预报……如果引申波幅与实际的波幅紧密相关，就应该观察与早期报道相似的现象。例如，波幅和价格之间的相反关系^[34]已经被专家大卫·温鲍姆（David Weinbaum）使用S&P100指数考察过了。他发现引申波幅的增长与市场价格的下降有着密切的联系，反之亦然。另外，从长期期权引申出来的波幅，在大多数的时间中，比从短期期权引申出来的波幅低，与均值回复保持一致。

期权

在过去的10年里，关于波幅本身不稳定的认识不仅仅影响了预报，也影响了期权定价和在这样情况下的风险管理，但是关于如何在这样的情况下操控风险的建议却很少。

作者和丹·加拉（Dan Galai）已经提议创造一个波幅指数，并且用波幅期权和期货来对冲变化。最近，巴黎交易期货市场（MONEP）、法国期货和期权交易所，已经引进了在这个方法基础上的波幅指数。^[35]这个想法是要构建一个指数，这个指数通过取具有不同到期日的期权的均值来暗示在接下来的30天内将要流行的波幅。

另一个引申波幅指数是波动率指数（VIX），由芝加哥期权交易所（CBOE）引进的。《金融时报》发表了来自于周二到周五的债券和股票市场风险衡量的相关波幅指数。

下一步应该是波幅期权的引进，这个对对冲期权资产组合和股份与债权的资产组合没有预料到的波幅的改变是有用的。

资料来源：梅纳克明·布伦纳：《不稳定力量的多变本质》，《商业日报》（南洲版）2001年10月16日。

链接

这篇文章讨论了几种估计波幅的方法。除了这一章已经提过的指数加权移动均值（EWMA）之外，它还集中在一些其他的方法上，即引申波幅（如果在市场上使用期权价格作为起点，可以转向BS模型，计算与现行价格保持一致的波幅；这个波幅就叫做引申波幅；相关期权的引申波幅可以是人们想要估计的波幅的很好的说明），和波幅指数（就像股票指数是市场上最重要的股票价格的指示一样，波幅指数是那个市场上波幅的指示；其中一些指数也可以使用指数期权的引申波幅来计算）。后者已经被证明是很有趣的测量，但是它们只是对于有限数量的股票指数来说是可以得到的。这些指数还说明了学术领域和交易发展的期权定价之间的联系。

20．5．4　例子

现在来说明BS模型。当然，可以只是在附录B中描述的Excel程序中输入数字，但是人工计算期权价值是有启发性的。也可以把答案与Excel程序的结果进行比较，来说明约数的影响。

假设想要计算拥有以下参数的买入期权的价值：S=$102，X=$100，σ=30%，r= 8%，q=1%，t=182天，大约是1/2年。通过下面的三个步骤来计算结算价：

第一步：使用参数，列出方程，得到：

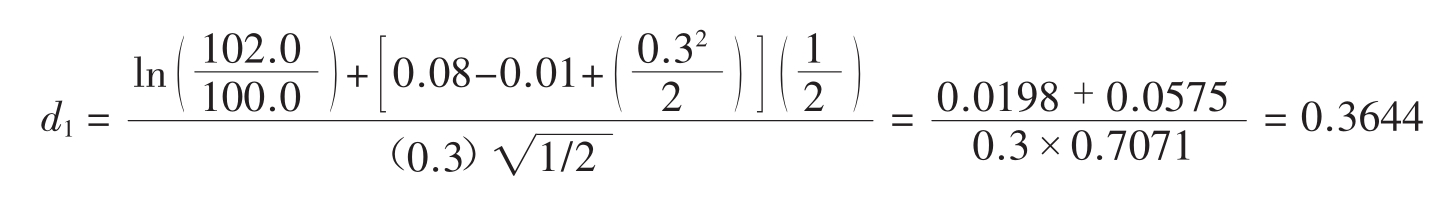
另外，从方程式20.16中，得到：

现在有d₁和d₂，已经可以计算N（d₁）和N（d₂）了。

第二步：确定N（d₁）和N（d₂）。不幸的是，期权价格对于N（d₁）和N（d₂）的估计是很敏感的。所以，达到高水平的准确是很重要的。附录提供了N（d）的价值，其中已有价值d精确到小数点后四位。计算的d₁和d₂的价值在这里并没有精确地给出。所以，需要在表中的N（d）的两个最近的值之间加入：

d_1H=0.365N（d_1H）=0.6424d_2H=0.155N（d_2H）=0.5616

d_1L=0.360N（d_1L）=0.6406d_2L=0.150N（d_2L）=0.5596

估计：

d₁=0.3644N（d₁）=？d₂=0.1522N（d₂）=？

d_1H，d_1L，d_2H和d_2L是附录中d₁和d₂最近的上方和下方的价值。H代表的是高的一边的价值，L代表的是低的一边的价值。插入的公式为：

注意只是给较低的价值N（d_L）加上了N（d_H）－N（d_L）的一部分，这一部分会随着d-d_L下降而变大。例如，如果d=d_H，就精确地得到N（d）=N（d_H）。如果d=d_L，精确地得到N（d）=N（d_L），正如期待的。所以，对于N（d₁），有：

类似地，对于N（d₂）我们有：

既然知道了N（d₁）和N（d₂），就准备好计算期权价格了。

第三步：计算结算价。

现在将N（d₁）和N（d₂）的价值代入方程式20.14：

c=（$102.00e^-0.01/2×0.6422）-（$100.00e^-0.08/2×0.5605）=$65.18-$53.85=$11.33

注意在使用182天到期的过程中，由附录B中Excel程序得到精确的计算为c=$11.31。严格说来，在BS模型的假设下，知道结算价应该是11.31美元，否则就会有套利。那在例子中与2美分的差距有没有关系呢？或许没有：实际上，人们可以怀疑2美分的差距是否达到足够弥补交易成本——真正的无摩擦市场是不存在的。

使用之前的数据和方程式20.18，可以计算看跌价格：

p=$100.00e^-0.08/2×（1.0-0.5605）-$102.00e^-0.01/2×（1.0-0.6422）

=$100.00×0.9608×0.4395-$102.00×0.9950×0.3578=$42.23-$36.31=$5.92

所以，布莱克—斯科尔斯的看跌价格大约为5.92美元。直接使用上面的参数和到期日182天，计算机程序得到的结果为5.91美元，这又是因为约数。

现在计算灵敏度就是一个很轻松的工作了：delta（所以想要对冲比率来创造动态的对冲资产组合）就是e^－qtN（d₁）或者0.9950×0.5605=$0.5577。所以，如果股价上升到103美元，期权价值会成为大约为$11.33+$0.5577=$11.89。这个期权的合成复制会包括（除了借入的资金）0.5577股份。同样的，这个期权的gamma为：

所以，如果想要在股价上升到103美元之后，得到新的期权的价值的二次近似值，就是c=c₀+Δ（S-S₀）+¹/₂Γ（S-S₀）²=11.33+0.5577（103-102）+0.008（103-102）²=$11.90。Excel的结果为11.96美元，所以需要对近似值很小心，即使是对相对较小的改变。

20．5．5　BS模型的实证证据以及局限

在确定期权价值方面BS模型有多准确呢？可以如BS模型描述的那样来计算期权的理论上的价值，并将其与观察到的市场价格进行比较。如果没有明显的差别，那么模型运转良好。一些实证研究已经测试了这个模型。总的说来，这些测试都是支持BS模型的。它对于较长到期（3个月到1年）来说运行良好，有适当的波幅和等价期权。但是，在短期期权的情况下，极高或者极低的波幅和在价内或者价外的期权，BS模型的表现就不是很好了。大多数知道的关于BS模型错误定价在一段时间内都是不稳定的。例如，高波幅的股票期权可能发现被BS模型在5年的时期内过高估价，却在另一个5年的时期内过低估价。

给出一个关于BS模型的一些重要实证研究的简短的回顾。布莱克—斯科尔斯（1972）发现BS模型倾向于对具有高变化的期权过高定价，对于具有低变化的期权过低定价。吉特金等人（Gultekin et al.，1982）发现了同样的结果，并且发现了BS模型高估价内期权的价值，但是低估价外期权的价值。麦克贝思和默维尔（Macbeth&Merville，1979）发现BS模型对于价内期权的估价高于市场，对于价外期权的估价低于市场。对于短期期权这种差别更加明显。更近的时候，朗和奥菲斯（Long&Officer，1997）调查了BS模型的错误定价与交易量之间的关系。他们的证据说明与较少交易的期权相比，交易频繁的买入期权的定价更加有效，而且有较低的误定价的错误。

尽管研究人员已经发现了一些偏见，但是BS模型仍然是解释期权价格行为的最好的模型之一。而且并不是每个BS价值的偏离都形成偏见：总体上来说，有三个范畴的解释：

■在应用模型的过程中有计算错误，或者使用了错误的输入项；

■观察到的市场价格在线外，违背了无套利规则；

■违背了BS模型的假设。

实际中，个体投资商会在第一个范畴中经常犯错误。如果认为第三个结论确实是可行的，就能够尝试将错误归结到BS模型的具体的假设。下面会给出一些例子，研究已经发现了对于BS模型的偏见的一些原因。现在的研究集中在三个问题上：收益率分布的形状，股价跳跃的可能性以及不一致波幅（Non-constant Volatility）。

第一个问题将会在下一节讨论。关于跳跃，可以说BS模型假设资产价格的连续变化，意味着如果指定资产值50美元，下个月值60美元，那么在那个月的某个时间，股价应该为50.01美元，50.02美元，等等：所有在50美元和60美元之间的价值都会出现。这就排除了估价在一个时间是50美元在下一个时间是60美元的情况。下面的情况是不现实的：如果重要的新信息到达了市场，那么资产价格将会跳跃（Jump）到它们的新价值并且跳过所有中间的价值。如果真的有这样的跳跃的可能性，例如，当石油公司在宣布债券是否成功的时候，BS模型就会低估变成价内的价外期权的可能（包括看跌期权和买入期权）。不一致波幅（或者标准偏差）在第703页脚注②和第705页脚注①中已经提到。当一个期权还剩3年的时间到期，波幅不太可能会在那个时期内保持一致，尽管注意到了短期的波幅的不确定影响与短期跳跃的影响相比要小。有时，模型会在波幅本身就是随机的（任意的）地方使用。这就要求更先进的数学；感兴趣的读者可看这一章末尾的参考文献。

波幅微笑

另外一个考察BS模型的有效性的方法是估计股票收益率的波幅。引申波幅基本上是通过转向BS模型和找到给予期权现行市场价格的波幅来得到的。所以，以市场中实际期望为计算的基础。在BS模型的假设条件下，期权的引申波幅不应该取决于具有相同到期日的级别，这一点可以比较容易地观察到。在实践中，其结果的形式并不是直线，而是“微笑”或者“讥笑”。对于股票和指数期权，拥有低执行价的期权的引申波幅比较高（深入价外的看跌期权和深入价内的买入期权），造成了图20.14（a）中的形态。外汇期权的行为有所不同：拥有高和低执行价的期权有较高的引申波幅，在图20.14（b）中表现出来（所以有了这名字波幅微笑（Volatility Smile））。

我们可以解释在图20.14中描述的部分错误。具有低执行价的股票期权相对昂贵（应该记住波幅对期权价值有正影响，所以高引申波幅意味着高价值）。这些市场价格暗示的股价崩溃的可能要比在BS模型假设的高。^[36]罗宾斯坦（Rubinstein，1994）把这种现象叫做“crash-o-phobia”。

图20.14　引申波幅

在BS模型第五个假设——对数正态分布——的部分，实践中经常受到违背。除了对市场崩溃的恐惧之外，另一个原因就是杠杆效应：杠杆效应会引起更加不稳定的股票价值（所以股票价格）作为对公司价格变化的反应。假设公司债务与公司总价值保持或多或少的一致，当股价下跌的时候，杠杆效应就会增加，也就增加了股票的波幅。

看外汇期权的时候（图20.14（b）），引申分布（Implied Distribution）暗示着高执行价和低执行价都对对数正态分布有了偏差。这是因为汇率的极度变化比在对数正态的情况下更可能发生；不考虑方向，汇率具有更高的显出跳跃的可能性（由于一些货币的外汇钉住——在跳跃结束时采用的政策），并且汇率的波幅比股票的波幅要更加不一致。然而尽管有这些局限，BS模型仍然被认为是十分成功的。

总结

使用期权定价方程式

期货协议期可以通过构建数据对冲的资产组合来定价，使用的是无套利原则。资产组合创造的权利和义务与期权合约使用的已知价格的资产，也就是期权合约的债券和指定资产是完全一致的。不同的指定资产的价值区别是由它们不同的持有成本造成的。

确定期权界限，使用期权的平价

买入期权最少值要0和现行股价减去贴现行使价的最大值，它的价格将会一直在指定资产之下。看跌期权最少值要0和贴现行使价减去现行股份价格的最大值，它的价格将会一直在贴现行使价之下。期权买卖平价建立了买入期权、看跌期权、指定资产和债券之间的关系。买入期权和特殊的债权与指定资产和买入期权是相等的。

使用二项式树形图来计算期权价格

概括用5个步骤的过程来确定期权价格：第一，假设股票价格只移动到两个未来价值中的一个；第二，到期的期权价格是从未来股票价格确定的；第三，建构股票和期权的资产组合；第四，交易具体数量的股票，叫做对冲比率，这样的未来收益是确定的；第五，使用标准净现值法来确定期权价格，这个模型可以简单地扩展到很多未来股票价格。有了股票价格，期待的股票的收益率并不直接影响期权价格。影响只是在观察到的现行股价中（S₀）。

使用布莱克—斯科尔斯期权定价模型来定价买入和看跌期权对于买入期权，根据BS模型价格应为：

c=Se^-qtN（d₁）-Xe^-rtN（d₂）

其中：

看跌期权的价格可以通过使用期权买卖平价来建立。这只能应用于欧式非股息支付期权：美式期权、权证和衍生工具期权都要求公式的调整。

讨论期权定价的实证证据

BS模型是一个成功的模型。但是在应用的时候应该小心：只有当输入项正确的时候，模型才能发挥功效。对于标准偏差的估计有着尤其大的影响，与其他的灵敏度相比，对于估计波幅（Vega）的灵敏度是很大的，估计本身经常也是不太确定的。BS模型的对数正态分布假设是存在问题的：有“商业公司破产恐慌”的证据，股票收益率分布的杠杆影响，以及极端收益率的频繁出现以及货币的跳跃。

关键词

延期交割678

基价677

二项式模型687

布莱克-斯科尔斯期权定价

模型（BS模型）696

交易延期678

连续时间685

持有成本模型673

聚集678

Delta 698

分散时间685

动态对冲672

指数加权移动均值704

无摩擦市场687

Gamma 699

对冲比率689

引申分布709

跳跃708

对数正态分布696

均值修正703

默顿模型696

货币性701

无套利670

不一致波幅708

期权定价界限678

期权买卖平价683

重组692

Rho 700

标准正态分布697

静态对冲671

衰减时间700

时间价值685

Vega 700

波动性峰值703

波幅微笑709

成本673

二项式树形图692

练习题

1．假设金子的现货价格为340美元每金衡制盎司。另外假设下面是你观察到的金子的期货价格：

a．计算每个期货协议期的基础。

b．如果无风险利率为3%，引申的金子的一年储藏成本是多少（以分数表示）？

2．使用套利表格，证明看跌期权价格一定是在执行价的贴现价值之下。也就是证明方程式20.7：

p₀≤X/（1+r）^t

3．建立二项式树形图，并且是用下面的信息为看跌期权定价：期权在两个时期之后到期，在每一个时期中，u=1.20，d=0.75；现行估计为100美元，行使价为92美元。无风险利率为每个时期3%，没有股息。

4．假设标准偏差是σ=30%，S₀=$100，X=$100，r=5%，q=3%，t=1/2，计算布莱克—斯科尔斯买入和看跌期权价格。

5．使用问题4中的信息，但是假设股价增长了1%达到101美元：

a．布莱克—斯科尔斯的新的买入和看跌期权的价格是多少？将你的结果与问题4中的结果进行比较。

b．使用delta公式（见方程式20.19）计算期权价格的变化。

c．使用delta的gamma公式（见方程式20.21）计算期权价格的变化。

d．在股价增长了10%达到110美元的基础上重新计算a、b、c部分。

若想获得练习题的参考答案，请访问Levy-Post投资网站，网址为：http://www.booksites.net/levy

参考文献

Black，F.and M.Scholes，1972，‘The Valuation of Option Contracts and a Test of Market Efficiency’，Journal of Finance，27（2），399-418.

Black，F.and M.Scholes，1973，‘The Pricing of Options and Corporate Liabilities’，Journal of Political Economy，81，637-654.

Chance，Don M.，2004，An Introduction to Derivatives and Risk Management，6th edn，London：South-Western.

Copeland，L.S.，2000，Exchange Rates and International Finance，3rd edn，Englewood Cliffs，NJ：Prentice-Hall.

Cox，J.C.，S.A.Ross and M.Rubinstein，1979，‘Option Pricing：A Simplified Approach’，Journal of Financial Economics，7，229-263.

Ehrhardt，M.C.，J.V.Jordan and R.A.Walking，1987，‘An Application of APT to Futures Markets：Test of Normal Backwardation’，Journal of Futures Markets，7（1），21-34.

Green，J.and E.Saunderson，1998，‘No Room at the Top’，Risk，11.

Gultekin，N.B.，J.Rogalski and S.M.Tinic，1982，‘Option Pricing Model Estimates: Some Empirical Results’，Financial Management，11，58-69.

Hull，J.，2003，Options，Futures and other Derivatives，5th edn，Englewood Cliffs，NJ：Prentice-Hall.Jackwerth，J.C.and M.Rubinstein，1996，‘Recovering Probability Distributions from Option Prices’，Journal of Finance，51（5），1611-1631.

Kolb，R.W.，2003，Futures，Options and Swaps，4th edn，Malden，MA:Blackwell.

Long，D.and D.Officer，1997，‘The Relation between Option Mispricing and Volume in the Black-Scholes Option Model’，Journal of Financial Research，20，1-12.

Macbeth，J.and L.Merville，1979，‘An Empirical Examination of the Black-Scholes Call Option Pricing Model’，Journal of Finance，34（5），1173-1186.

Merton，R.，1973，‘Theory of Rational Option Pricing’，Bell Jlournal of Economics and Management Science，4，141-183.

Robertson，Malcolm J.，1990，Directory of World Futures and Options，Englewood Cliffs，NJ：Prentice-Hall.

Rubinstein，M.，1994，‘Implied Binominal Trees’，Journal of Finance，49（3）,771-818.

Tyson-Quah，K.，1997，‘Clearing the Way’，Risk，10，8.

【注释】

[1]Where at least one of these payments is non-zero.

[2]Note that this definition is rather general:an arbitrage opportunity also exists when a portfolio can be constructed that yields a cash inflow today and with no risk of future losses.By lending all the proceeds received today,one will receive a positive payoff in the future,again with zero net investment.So,this is also an arbitrage opportunity.See Section 11.2.1 for some examples.

[3]In the example above，the portfolio with a stock,a put and borrowed money is a synthetic replica for the call option.

[4]One should bear in mind that hedging and arbitrage are related,but different,strategies:in arbitrage,one tries to profit form pricing errors or differences in the market without taking on price risk,while hedging is intended to eliminate price risk on an existing exposure.However,since any arbitrage trade is supposed to be riskless,the positions taken should hedge each other,hence the use of the term‘hedge’in this context.

[5]Forward prices are often regarded as equivalent to futures prices.But,as the time to maturity increases the difference in the manner that the two contracts are settled（forwards at maturity,being an OTC product,and futures during the life of the contract as well as at maturity because they’re marked to market）results in differences in the timing of the different cash flows involved,a difference that is often non-negligible for the amounts usually involved with these kinds of contracts.

[6]For convenience,we assume that the dividend is paid at the end of the period.If not,we should correct for interest on the dividend.

[7]At maturity,futures and spot prices will always be equal.Buying a futures contract that matures immediately is no different than buying the asset on the spot market,see Chapter 19.

[8]If we have continuously compounded dividend and interest,then the equation can also be rewritten as F₀=S₀e^（r-d）t, where t is the fraction of a year between the two periods and r-d is the total rate of return on the stock minus the dividend rate of return components-that is,the rate of return that is due to capital gains only.

[9]This might not hold when market conditions are expected to change in the future,for instance due to decreased supply（think of a major refinery closing for maintenance,diminishing oil products supply）.These forecastable changes are a common occurrence in some markets.

[10]See Chapter 6 for a description of the MMI.

[11]With annualised continuous interest rates,this formula can be written as F₀=S₀ e^（rL-rf）twhere t is the time,usually given as a fraction of a year.

[12]Readers interested in this subject are referred to L.S.Copeland（2000），Exchange Rates and International Finance，3rd edn，Englewood Cliffs，NJ:Prentice-Hall.pp.435-466.

[13]Basis is computationally the same as the concept of intrinsic value used in options,introduced in Chapter 19. However,American-style options can be exercised immediately,so the intrinsic value can actually be received in cash.With the basis,this is impossible,because the settle date is fixed and is in the future.

[14]We use the term‘price’rather than‘premium’because these boundaries apply throughout the life of the option，not just on the initial purchase date.

[15]Buying a zero-coupon bond is equivalent to lending money,and selling a zero-coupon bond is equivalent to borrowing money.

[16]Most often,the term‘time value’refers to discounting future cash flows.When related to options,time value has a different meaning.It is the value of the option related to the chance that the option may go in the money（or further in the money,if it is already in the money）.

[17]If d>1+r,then the stock will always yield more than the risk-free rate.In this case,everyone would borrow at r and invest in stock,yielding an arbitrage profit.If u<1+r,then the stock will always yield less than the risk-free rate.In this case,everyone would short-sell the stock and lend at r,yielding an arbitrage profit.

[18]In particular，see Hull（2003），Options，Futures and Other Derivatives，5th edn，Englewood Cliffs，NJ：Prentice-Hall，pp.355-358 and p.369，and Cox et al.（1979），‘Option Pricing:A Simplified Approach’，Journal of Financial Economics，7，pp.229-263.

[19]Unlike stock splits，which lead to a correction of the exercise price.

[20]This assumes that the investor knows the parameters of the binominal model，and that this model is correct.

[21]However，one can derive an implicit expected return in the BS model，but the formula does not take it as an input: rather，it is a side result of the assumptions concerning the distribution.

[22]A log-normal distribution is skewed positively，in contrast to a normal distribution，which has no skewness.This reflects the fact that one can have returns of，for example，+200%，while the underlying asset cannot achieve a return below-100%.See，for instance，Hull（2003）and Kolb（2003），for more on this distribution and its place in the derivation of the BS model.

[23]Black and Scholes on the one hand,and Merton on the other,published their findings almost at the same time while they were working independently on option pricing.We will use the formulas proven by Merton,which are more general. However,Black and Scholes got their article published first,and hence the model is often referred to as the Black-Scholes model,even though for this version the term‘Merton model’is more appropriate.For the sake of brevity,and because of the general use of the term‘Black-Scholes model’,we will use‘BS model’for Merton’s extended model as well.

[24]Unless indicated otherwise,we drop the subscripts,i.e.c=c₀,S=S₀ and p=p₀ from here on,because we are no longer in a discrete time model.

[25]N（d）is the area under the standard bell or normal curve up to point d.N（d）can be solved using a computer or can be estimated using standard statistical tables,as discussed below.

[26]In general,N（-d）=1-N（d）because of the symmetry of the normal distribution.

[27]Formally,delta is the first derivative of c to S,DC/DS.

[28]Using calculus,it is the second derivative of the call price to the stock price.

[29]All sensitivities,except gamma,are based on linear approximations,but to limit the mistakes of these approximations, one can also look at higher-order approximations.Gamma is the most commonly used,but not the only one that large investors may want to look into.

[30]Some authors define it the other way around,namely X/S,and sometimes the difference between X and S is referred to as moneyness.

[31]In this respect，the continuously compounded dividend yield differs from the discrete dividend yield discussed in Chapter 15.If a dividend is paid m times a year and the discrete dividend yield is R_m per cent,the continously compounded dividend yield is q=m ln（1+R_m/m）.

[32]Actually，this problem has two sides to it:on the one hand,we estimate the variance at this moment using historical data that may reflect a different variance from the current one.On the other hand,we assume that，once we’ve calculated the current variance，it remains constant for the rest of the life of the option.For options with long remaining maturities（especially LEAPS），the second problem needs to be addressed as well.This leads to econometric methods that are outside the scope of this book.

[33]It becomes even more problematic if trading was halted for some days,which is what happened on the New York exchanges in the aftermath of 11 September.There is no way of knowing what the returns and volatility would have been if trading in New York hadn’t stopped.In this example,we assume that trading continued（e.g.stocks listed in Europe,Asia and Latin America）.

[34]Author note:volatility is historically high and changing in times of economic crisis.

[35]Author note:since this article was written,this exchange has been incorporated into Euronext Paris.

[36]More formally,we could derive an implied distribution from these data（calculate the distribution of returns from the stock prices）.In other words,we can recover the market opinion about the chance of a certain S at maturity.This is a dataintensive matter,and requires some assumptions itself.See Rubinstein（1994）and Jackwerth and Rubinstein（1996）.