第七章 直接民主制中的公共选择
在一些公共选择经济学家看来,有些时候,经济中的所有个人都要参与委员会组织的投票过程,以一人一票的方式决定某项备选议案是否能够成为最终获胜的议案,进而得出某一政治问题的解决方案。这种由所有个人参与其中的政治形式,也被称为直接民主制。本章在直接民主制条件下尝试分析“经济人”,在这里通常是投票人的行为选择。
第一节 中位数投票人定理——一维议案
中位数投票人定理作为公共选择经济学的一个早期的重要定理,是由英国北威尔士大学教授邓肯·布莱克(1948a)证明的。布莱克认为,在单一的议案维度上,如果所有投票人的偏好都能够满足单峰偏好假设,那么,简单多数规则将会帮助委员会寻找到某一均衡的投票结果。
一、单峰偏好假设与中位数投票人定理
下面,我们来熟悉一下公共选择经济学关于议案维度、理想议案和单峰偏好假设等概念的理解。
1.一维议案
学者们常常借用维度这一概念来描述所有提交委员会讨论的备选议案。所谓一维议案指的是,可以把所有备选议案表示成一个一维向量,使得人们能够在一维的坐标轴上把全部备选议案排列开来。
2.理想议案
任选某一位投票人i,如果我们能够为i寻找到某一项备选议案xi*,当且仅当对于任意其他的备选议案x,且x≠xi*,都有xi*![]() ix成立,我们就说xi*是i的理想议案。
ix成立,我们就说xi*是i的理想议案。
3.单峰偏好假设
单峰偏好假设要求,在所有的备选议案当中,与i的理想议案xi*更加接近的备选议案,能够给i带来更高水平的效用。如果所有备选议案都能够在一维坐标轴上排列开来,并且能够在该坐标轴上为i寻找到他的理想议案xi*,令y和z是其他的任意两项备选议案,且y≠xi*,z≠xi*,并且在一维的坐标轴上y和z或者同时处于xi*的左侧,或者同时处于xi*的右侧,则i的偏好在单一的议案维度上是单峰的,当且仅当y比z更接近xi*时,有y![]() iz成立。由此可见,单峰偏好假设是对任意投票人i的偏好序施加的一种约束,它限制了i关于所有备选议案可能采取的偏好类型。
iz成立。由此可见,单峰偏好假设是对任意投票人i的偏好序施加的一种约束,它限制了i关于所有备选议案可能采取的偏好类型。
如果所有备选议案都能够在一维的坐标轴上予以表示,假设有i和j两位投票人,其中i比较倾向于某一折中的观点,而j则更倾向于议案维度上的两个极端。那么,在单一的议案维度上描述i和j两位投票人的效用函数ui和uj,ui和uj分别代表排列在一维议案维度上的不同备选议案给i和j两位投票人带来的效用水平,如图7-1所示。
图7-1 一维议案及投票人的效用函数
在图7-1中,投票人i的偏好是单峰的,而投票人j的偏好则不满足单峰偏好假设。
在所有的备选议案中为所有投票人寻找各自的理想议案(x1*,x2*,…,xm*,…,xn*),并将其排列在一维坐标轴上,令nL表示排列在xm*左侧包括xm*在内的理想议案的数量,令nR表示排列在xm*右侧包括xm*在内的理想议案的数量,当且仅当nL≥![]() 且nR≥
且nR≥![]() 时,称xm*为中位置,称xm*对应的投票人m为中位数投票人。公共选择经济学认为,如果可以找到一个单一的议案维度,使得在这个议案维度上描述所有备选议案时,每一位投票人的偏好都能够满足单峰偏好假设,那么,中位数投票人m的理想议案xm*将成为最终获胜的议案。
时,称xm*为中位置,称xm*对应的投票人m为中位数投票人。公共选择经济学认为,如果可以找到一个单一的议案维度,使得在这个议案维度上描述所有备选议案时,每一位投票人的偏好都能够满足单峰偏好假设,那么,中位数投票人m的理想议案xm*将成为最终获胜的议案。
定理7.1(一维议案的中位数投票人定理):如果所有备选议案都可以在单一的议案维度上予以表示,并且所有投票人的偏好在该议案维度上都是单峰的,那么,中位数投票人的理想议案在简单多数规则的约束下不会失败。
考虑一种简单的情况。假设有i1、i2、i3、i4、i5五位投票人参与委员会的投票过程。当所有备选议案都能够在一维坐标轴上予以呈现,并且所有投票人的偏好都满足单峰偏好假设的时候,五位投票人的效用函数可以被表示如下(见图7-2):
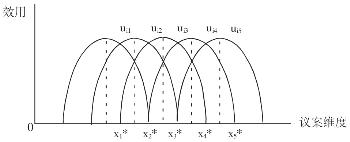
图7-2 中位数投票人的选择——一维议案
在图7-2中,x1*、x2*、x3*、x4*、x5*分别代表i1、i2、i3、i4、i5五位投票人的理想议案,其中x3*是中位数投票人i3的理想议案,满足nL≥n 且nR≥2![]() 。在一维的议案维度上,中位数投票人i3的理想议案x3*处于所有投票人理想议案的中间位置上。
。在一维的议案维度上,中位数投票人i3的理想议案x3*处于所有投票人理想议案的中间位置上。
因为所有投票人的偏好都满足单峰偏好假设,所以,相对于x3*左侧的任何备选议案,x3*至少可以得到i3,i4和i5三位投票人的支持;相对于x3*右侧的任何备选议案,x3*至少可以得到i3,i1和i2三位投票人的支持。因此,在简单多数规则的约束下,中位数投票人i3的理想议案x3*与任何其他备选议案一起提交委员会讨论时,x3*都能够得以通过。
二、循环的可能性
前文集中讨论了如果可以找到一个单一的议案维度,使得所有投票人的偏好都满足单峰偏好假设的要求,那么,在简单多数规则的约束下,委员会能够达成一个均衡的投票结果,并使得中位数投票人m的理想议案xm*成为最终获胜的议案。一些公共选择经济学家还分析了单峰偏好假设不能得到满足的情况,他们的结论是,即便可以找到一个一维的议案维度,如果不是所有投票人的偏好都满足单峰偏好假设,那么,委员会的投票过程也很可能陷入一种无休止的循环之中。当出现循环问题的时候,对于任意一项备选议案x,都能够找到某一其他的备选议案x′,且x′≠x,使得委员会就x和x′两项议案进
行投票时,有x′战胜x。
大量的公共选择经济学文献分析了循环问题出现的可能性,并进一步讨论了怎样才能避免循环问题的出现。甚至还有一些学者,比如戈登·塔洛克,能够清醒地认识到,现实的政治过程并没有像公共选择经济学家预期的那样经常出现循环问题,从而迫使学者们正视理论与现实之间存在的差距。诸如此类的问题将在第六篇探讨阿罗不可能定理与公共选择经济学中的循环问题时再一一予以介绍。在这里,我们暂时把目光集中在以下命题上,单峰偏好假设的违背可能会导致循环问题的出现。
假设有一个只存在a、b、c三位投票人的委员会,借助简单多数规则就A、B、C三项备选议案组织投票过程。假设三位投票人的偏好情况可以表示如下:
A![]() aB
aB![]() aC
aC
B![]() bC
bC![]() bA
bA
C![]() cA
cA![]() cB (7.1)
cB (7.1)
可见,在A、B、C三项备选议案中,A是投票人a的理想议案;B是投票人b的理想议案;C是投票人c的理想议案。在如下的坐标图(见图7-3)中,将a、b、c三位投票人关于A、B、C三项备选议案的偏好情况粗略地表示出来,有:
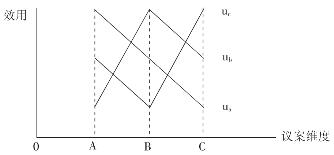
图7-3 单峰偏好假设的违背
如图7-3所示,考虑投票人c关于A、B、C三项备选议案的偏好序C![]() c A
c A![]() cB,在单一的议案维度上,C是投票人c的理想议案,A和B两项备选议案都位于C的左侧,并且A与C之间的距离要大于B与C之间的距离,但是,与B相比,投票人c却更偏好于A,可见,c的偏好违背了单峰偏好假设。由上述三位投票人的偏好序可知,无论在一维坐标轴上怎样排列A、B、C三项备选议案,总会存在一位投票人的偏好违背单峰偏好假设。无法找到某一单一的议案维度,使得在该议案维度上描述A、B、C三项备选议案时,每一位投票人的偏好都能够满足单峰偏好假设。
cB,在单一的议案维度上,C是投票人c的理想议案,A和B两项备选议案都位于C的左侧,并且A与C之间的距离要大于B与C之间的距离,但是,与B相比,投票人c却更偏好于A,可见,c的偏好违背了单峰偏好假设。由上述三位投票人的偏好序可知,无论在一维坐标轴上怎样排列A、B、C三项备选议案,总会存在一位投票人的偏好违背单峰偏好假设。无法找到某一单一的议案维度,使得在该议案维度上描述A、B、C三项备选议案时,每一位投票人的偏好都能够满足单峰偏好假设。
在上述只存在a、b、c三位投票人和A、B、C三项备选议案的简单经济中,因为三位投票人的偏好序采取如(7.1)式所描述的形式,所以,当委员会就A和B两项备选议案进行讨论的时候,a和c会投票赞成议案A,只有b会投票赞成议案B,根据简单多数规则,议案A能够战胜议案B,委员会关于A 和B两项备选议案的排序为A![]() B;当委员会就B和C两项备选议案进行讨论时,a和b会投票赞成议案B,只有c会投票赞成议案C,根据简单多数规则,议案B能够战胜议案C,委员会关于B和C两项备选议案的排序为B
B;当委员会就B和C两项备选议案进行讨论时,a和b会投票赞成议案B,只有c会投票赞成议案C,根据简单多数规则,议案B能够战胜议案C,委员会关于B和C两项备选议案的排序为B![]() C;当委员会就A和C两项备选议案进行讨论时,b和c会投票赞成议案C,只有a会投票赞成议案A,根据简单多数规则,议案C能够战胜议案A,委员会关于A和C两项备选议案的排序为C
C;当委员会就A和C两项备选议案进行讨论时,b和c会投票赞成议案C,只有a会投票赞成议案A,根据简单多数规则,议案C能够战胜议案A,委员会关于A和C两项备选议案的排序为C![]() A。可见,在简单多数规则的约束下,当委员会就任意两项备选议案进行投票的时候,没有一项议案是不能被打败的,投票结果将会在A、B、C三项备选议案之间不断地循环。公共选择经济学认为,如果不是所有投票人的偏好都满足单峰偏好假设,那么,委员会采用简单多数规则组织的投票过程中就有可能出现循环问题。[1]
A。可见,在简单多数规则的约束下,当委员会就任意两项备选议案进行投票的时候,没有一项议案是不能被打败的,投票结果将会在A、B、C三项备选议案之间不断地循环。公共选择经济学认为,如果不是所有投票人的偏好都满足单峰偏好假设,那么,委员会采用简单多数规则组织的投票过程中就有可能出现循环问题。[1]
但是,即便违背单峰偏好假设,也并不意味着循环问题就一定会出现,循环问题能否出现还要依赖于每一位投票人偏好序的具体形式。后文讨论简单多数规则定理时还可以发现,单峰偏好假设并不是简单多数规则约束下均衡投票结果存在的必要条件。
第二节 中位数投票人定理——多维议案
与上一节着力分析的单峰偏好假设相比,在一些公共选择经济学家看来,议案的单一维度假设更加缺乏现实性。在现实的政治生活中,委员会讨论的备选议案往往是多维度的。比如,当所有投票人就某一公共物品的供给问题进行讨论时,一些投票人反对继续增加该公共物品的供给数量,可能是因为他们考虑到为弥补其生产成本必须加重人民的税收负担,从而造成社会矛盾激化。也可能是因为他们认为公共物品的供给已经造成了社会资源浪费;而另一些投票人支持继续增加该公共物品的供给数量,可能是因为他们考虑到其供给数量尚且不足以满足人们当前的需要,也可能是因为他们考虑到该公共物品的生产对经济发展会起到带动作用。再比如,当委员会就本国军队的规模进行讨论的时候,一些投票人赞成大规模缩减军队规模,可能是因为他们考虑到过度的军费开支不利于社会资源的合理利用,也可能是因为他们考虑到国际舆论的巨大压力;而另一些投票人赞成继续扩大军队规模,可能是出于对日渐严峻的国际政治形势方面的考虑,也可能是出于缓解国内矛盾方面的考虑。
当委员会讨论的所有备选议案不能用单一的议案维度予以表示时,C.R.普洛特(1967)证明,如果可以找到某一项备选议案,使得该备选议案对于一位并且只有一位投票人来说是理想议案,相对于该投票人来说,其余的偶数位投票人都能够在每一个议案维度上被划分成利益刚好对立的两两一对的话,那么,在简单多数规则的约束下,一定存在一个均衡的投票结果。在公共选择经济学中,这种对投票人偏好分布强加的严格的对称性假设,也被称为普洛特“完美平衡”条件。
考虑只存在x1和x2两个议案维度的简单情况,假设有a、b、c、d、e五位投票人,A、B、C、D、E分别代表上述五位投票人的理想议案。假设在x1—x2议案空间中,所有投票人的无差异曲线都是圆形的,每一位投票人都根据其他的备选议案与自己理想议案的距离来判断该备选议案能够带来的效用水平,与自己的理想议案距离更近的备选议案能够带来更高水平的效用。依照C.R.普洛特(1967)得出的结论,当五位投票人的理想议案在x1—x2议案空间中的位置采取类似图7-4中所描述的形式时,委员会能够在简单多数规则的约束下挑选出最终获胜的议案——E。
图7-4 中位数投票人的选择——多维议案
在上述存在x1和x2两个维度的议案空间里,a与b、c与d是两对利益相互对立的投票人,相对于议案E来说,如果存在其他的某项备选议案能够提高利益相互对立的一对投票人中任意一位投票人的效用水平,那么,它必然会使另一位投票人的利益遭受损害。普洛特认为,在上述简单的情况下,投票人e的理想议案E将会成为最终获胜的议案。考虑任意其他的备选议案,比如投票人a的理想议案A,与议案E相比,a会选择支持议案A。当委员会就A和E两项备选议案进行讨论的时候,因为a与b两位投票人的利益是相互对立的,所以b一定会投票支持议案E。如果c与d中的任意一位投票人,比如c会投票支持议案A,因为c与d两位投票人的利益也是相互对立的,所以d一定会投票支持议案E。可见,当A和E两项备选议案被同时提交委员会讨论的时候,议案A将会得到a和c两位投票人的支持,而议案E将会得到e、b、d三位投票人的支持,根据简单多数规则的要求,E将成为最终获胜的议案。只要投票人总是成对增加,在如图7-4所示的议案空间中,每一对投票人的理想议案总是落在过E点的直线上,且分布在E点两侧,普洛特“完美平衡”条件就不会被打破,议案E仍然是简单多数规则约束下委员会最终通过的议案。当普洛特“完美平衡”条件能够得到满足时,在议案空间中寻找每一对利益相互对立的投票人,连接他们的理想议案,我们可以发现,E点是所有方向上的中位点。
在公共选择经济学中,关于多维议案条件下委员会均衡投票结果存在性的分析,被称为多维议案的中位数投票人定理,这一定理是由戴维斯、德格鲁特和希尼奇(1972)证明的。假设无法在一维的议案维度上描述所有的备选议案,这里仍然考虑只存在x1和x2两个议案维度的简单情况,假设在x1—x2议案空间中,任意投票人的无差异曲线是一组以他自己的理想议案为圆心的圆,我们可以利用某项备选议案与该投票人理想议案之间的距离来判断他对于该项议案的满意程度,与他的理想议案距离越近的备选议案给他带来的效用水平越高。给定所有投票人的理想议案,假设存在某位投票人e的理想议案E,在x1—x2议案空间中,E点是所有方向上的中位点。过E点任意做一条直线WW,令nR表示理想议案落在直线WW及其右下方的投票人人数,令nL表示理想议案落在直线WW及其左上方的投票人人数。因为E点是所有方向上的中位点,所以有nR≥![]() 且nL≥
且nL≥![]() 成立。下面我们来简单介绍多维议案的中位数投票人定理及其证明过程。
成立。下面我们来简单介绍多维议案的中位数投票人定理及其证明过程。
假设无法在一维坐标轴上描述委员会讨论的所有备选议案,在这里,我们仍然考虑只存在x1和x2两个议案维度的简单情况,利用x1—x2议案空间来证明多维议案的中位数投票人定理。
1.定理的充分性证明
下面我们来尝试证明,如果E点在x1—x2议案空间中是所有方向上的中位点,那么,当委员会采用简单多数规则组织投票过程的时候,议案E不可能被任何其他备选议案打败。
证明:在x1—x2议案空间中寻找到E点,使得E点在所有方向上都是中位点。任取一项备选议案Z,且Z≠E,令其在x1—x2议案空间中的位置为Z点。连接Z点和E点,过E点画一条垂直于ZE的直线WW。如图7-5所示。
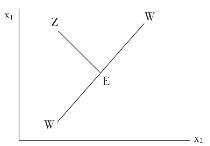
图7-5 多维议案的中位数投票人定理——充分性证明
因为Z点是任取的,所以,如果E点在x1—x2议案空间中是所有方向上的中位点,根据简单多数规则,它不可能被任何其他备选议案打败。
2.定理的必要性证明
下面我们来尝试证明,对于x1—x2议案空间中的任意一点Z,如果过Z点有直线WW不能够同时满足nR≥![]() 和nL≥
和nL≥![]() ,那么,在简单多数规则的约束下,Z点所代表的议案不可能成为最终获胜的议案。
,那么,在简单多数规则的约束下,Z点所代表的议案不可能成为最终获胜的议案。
证明:在x1—x2议案空间中任取一点Z,Z点代表备选议案Z的位置。过Z点做一条直线WW,使得理想议案落在直线WW及其右下方的投票人人数满足nR<![]() ,理想议案落在直线WW及其左上方的投票人人数满足n1L>。将直线WW向左上方移动,直到达到W′W′的位置,使得理想议案落在直线W′ W′及其右下方的投票人人数满足n′R≥
,理想议案落在直线WW及其左上方的投票人人数满足n1L>。将直线WW向左上方移动,直到达到W′W′的位置,使得理想议案落在直线W′ W′及其右下方的投票人人数满足n′R≥![]() ,理想议案落在直线W′W′及其左上方的投票人人数满足n′L≥
,理想议案落在直线W′W′及其左上方的投票人人数满足n′L≥![]() 。将以上分析制成图(见图7-6),有:
。将以上分析制成图(见图7-6),有:
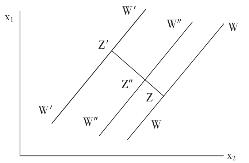
图7-6 多维议案的中位数投票人定理——必要性证明
在图7-6中,直线WW与W′W′是平行的,过Z点做直线ZZ′,使得ZZ′与直线WW和W′W′垂直,且Z′为ZZ′与W′W′的交点。任取一条直线W″W″,令其平行于WW和W′W′,并且位于WW和W′W′两条直线之间,W″W″与ZZ′的交点为Z″。
以上在只存在x1和x2两个议案维度的情况下,简单介绍了多维议案的中位数投票人定理及其证明过程。上述证明过程也可以推广到存在两个以上议案维度的情况。
当然,多维议案的中位数投票人定理是否能够成立,还要依赖于在所有的备选议案中是否能够寻找到类似于图7-4中E点所代表的议案,使得E点是议案空间中所有方向上的中位点。如果不存在类似于E的备选议案,当存在a、b、c三位投票人,使得其理想议案A、B、C在x1—x2议案空间恰好构成某个三角形的顶点时,如图7-7所示:
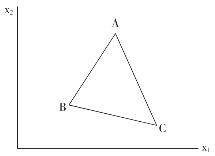
图7-7 多维议案条件下的循环问题
在图7-7所描述的情况下,对于x1—x2议案空间中的任意一项备选议案Z,都能够找到其他的某一备选议案Z′,使得Z′与其中两位投票人理想议案的距离更近。在简单多数规则的约束下,委员会组织的投票过程将会再次陷入循环问题之中。
第三节 极值限制与简单多数规则定理
除了前文论述过程中所使用的空间模型以外,公共选择经济学家还比较关心如何由“经济人”的行为选择分析推导出某些令人感兴趣的结论,而不是借助空间定义和几何知识。像通常的西方主流经济学家所做的那样,在这里,我们任取一位政治领域中的“经济人”i,假设i的偏好序能够满足一系列的理性公理假设,包括完备性、自返性、传递性。
iz成立,那么,一定有x![]() iz成立。
iz成立。
公共选择经济学秉承西方主流经济学的“经济人”假设,认为任意投票人i的偏好序都能够满足上述三个理性公理假设。因此,当i参与委员会就所有备选议案组织的投票过程时,这些备选议案在i的偏好序中是作为某一序关系存在的。其中排在最前面的议案能够使i的效用水平达到最高,这一议案就是i的理想议案。如果可能的话,任意投票人i的理想议案同时也是他的最优选择。按照这一研究思路,在简单多数规则的约束下,如果能够从总体上把所有备选议案定义为某一序关系,那么,排在最前面的议案就是委员会最终获胜的议案。
一、极值限制
下面我们着手讨论,当委员会采用简单多数规则的时候,在何种情况下才能从总体上为所有备选议案定义某一序关系。为此,一些公共选择经济学家还引入了关于个人偏好序的另一个限制条件——极值限制公理假设。[2]
极值限制公理假设:给定委员会讨论的所有备选议案,对于其中的任意三项备选议案x、y和z,如果存在某位投票人i,i的偏好序为x![]() iy和y
iy和y![]() iz,那么,对于每一位更加偏好议案z而非议案x的投票人j,j的偏好序一定满足z
iz,那么,对于每一位更加偏好议案z而非议案x的投票人j,j的偏好序一定满足z![]() jy和y
jy和y![]() jx。
jx。
可见,极值限制公理假设限制了委员会中所有投票人的偏好类型,如果存在投票人i,且i的偏好序可以表示为x![]() iy
iy![]() iz,那么,就不允许任何其他投票人j的偏好序采取y
iz,那么,就不允许任何其他投票人j的偏好序采取y![]() jz
jz![]() jx,或z
jx,或z![]() jx
jx![]() jy,或z
jy,或z![]() jx~jy,或z~jy
jx~jy,或z~jy![]() jx的形式,其中j≠i;又因为当投票人i的偏好序为x
jx的形式,其中j≠i;又因为当投票人i的偏好序为x![]() iy
iy![]() iz时,允许存在偏好序为z
iz时,允许存在偏好序为z![]() i′y
i′y![]() i′x的投票人i′,所以,不允许在委员会中出现的偏好类型还有x
i′x的投票人i′,所以,不允许在委员会中出现的偏好类型还有x![]() jz
jz![]() jy,y
jy,y![]() jx
jx![]() jz,x~jy
jz,x~jy![]() jz和x
jz和x![]() jy~jz。
jy~jz。
虽然公共选择经济学家在引入极值限制公理假设的时候,尽量做到避免采用空间词汇和几何知识,但是,这一假设条件对于所有投票人的偏好类型所采取的限制措施还是让我们联想到一维议案的单峰偏好假设。即便如此,极值限制公理假说也并不等同于单峰偏好假设。当存在偏好序为x![]() iy
iy![]() iz的投票人i时,极值限制公理假说并没有排除那些认为z与x两项备选议案无差异的偏好类型,因此,这一假设条件允许存在投票人i′,且i′的偏好序为z~i′x
iz的投票人i时,极值限制公理假说并没有排除那些认为z与x两项备选议案无差异的偏好类型,因此,这一假设条件允许存在投票人i′,且i′的偏好序为z~i′x![]() i′y。此时,如果在一维的议案维度上描述x、y、z三项备选议案,那么,对应x和z两项备选议案,投票人i′的效用函数将会出现双峰,且x和z两项备选议案给i′带来的效用是相等的。可见,极值限制公理约束了其偏好序为z
i′y。此时,如果在一维的议案维度上描述x、y、z三项备选议案,那么,对应x和z两项备选议案,投票人i′的效用函数将会出现双峰,且x和z两项备选议案给i′带来的效用是相等的。可见,极值限制公理约束了其偏好序为z![]() i′y,x
i′y,x![]() i′y的投票人i′,当在一维坐标轴上描述他的效用函数时,x和z两项备选议案所对应的双峰必然是等高的,如图7-8所示。
i′y的投票人i′,当在一维坐标轴上描述他的效用函数时,x和z两项备选议案所对应的双峰必然是等高的,如图7-8所示。
图7-8 极值限制公理允许存在的双峰偏好
二、简单多数规则定理
公共选择经济学认为,当所有投票人的偏好序都能够同时满足完备性、自返性和传递性等理性公理假设,并且符合极值限制公理假设的要求时,在简单多数规则的约束下,可以从总体上为所有备选议案定义某一序关系![]() ,也就是说,委员会对所有备选议案的排序也能够同时满足完备性、自返性和传递性等理性公理假设的要求,其中排在最前面的议案能够在委员会的讨论中获得通过。上述观点在公共选择经济学中被认为是简单多数规则定理的一项重要内容。在介绍简单多数规则定理及其证明过程之前,我们先来描述,当所有投票人的偏好序都能够同时满足完备性、自返性、传递性和极值限制公理假设的要求时,关于任意三项备选议案x、y和z允许存在的偏好类型。
,也就是说,委员会对所有备选议案的排序也能够同时满足完备性、自返性和传递性等理性公理假设的要求,其中排在最前面的议案能够在委员会的讨论中获得通过。上述观点在公共选择经济学中被认为是简单多数规则定理的一项重要内容。在介绍简单多数规则定理及其证明过程之前,我们先来描述,当所有投票人的偏好序都能够同时满足完备性、自返性、传递性和极值限制公理假设的要求时,关于任意三项备选议案x、y和z允许存在的偏好类型。
假设委员会中至少存在一位投票人i,且i的偏好序采取如下的形式:
偏好序Ⅰ:x![]() iy
iy![]() iz。令nⅠ代表偏好序可以表示为x
iz。令nⅠ代表偏好序可以表示为x![]() iy
iy![]() iz的投票人人数,且nⅠ≥1;
iz的投票人人数,且nⅠ≥1;
因为所有投票人的偏好序都满足极值限制公理假设的要求,所以,其他投票人i′可能会采取如下五种类型的偏好序,其中i′代表委员会中除i以外的任意其他投票人:
偏好序Ⅱ:z![]() i′y
i′y![]() i′x。令nⅡ代表偏好序可以表示为z
i′x。令nⅡ代表偏好序可以表示为z![]() i′y
i′y![]() i′x的投票人人数;
i′x的投票人人数;
偏好序Ⅲ:y![]() i′z~i′x。令nⅢ代表偏好序可以表示为y
i′z~i′x。令nⅢ代表偏好序可以表示为y![]() i′z~i′x的投票人人数;
i′z~i′x的投票人人数;
偏好序Ⅳ:z~i′x![]() i′y。令nⅣ代表偏好序可以表示为z~i′x
i′y。令nⅣ代表偏好序可以表示为z~i′x![]() i′y的投票人人数;
i′y的投票人人数;
偏好序Ⅴ:z~i′x~i′y。其偏好序可以表示为z~i′x~i′y的投票人也被视为弃权者,令nⅤ代表选择弃权的投票人人数。
比较x和y两项备选议案,令n(x![]() iy)表示为议案x而非议案y投赞成票的投票人人数,有n(x
iy)表示为议案x而非议案y投赞成票的投票人人数,有n(x![]() iy)=nⅠ+nⅣ;令n(y
iy)=nⅠ+nⅣ;令n(y![]() ix)表示为议案y而非议案x投赞成票的投票人人数,有n(y
ix)表示为议案y而非议案x投赞成票的投票人人数,有n(y![]() ix)=nⅡ+nⅢ。其中,i代表委员会中的任意投票人。
ix)=nⅡ+nⅢ。其中,i代表委员会中的任意投票人。
比较x和z两项备选议案,令n(x![]() iz)表示为议案x而非议案z投赞成票的投票人人数,有n(x
iz)表示为议案x而非议案z投赞成票的投票人人数,有n(x![]() iz)=nⅠ;令n(z
iz)=nⅠ;令n(z![]() ix)表示为议案z而非议案x投赞成票的投票人人数,有n(z
ix)表示为议案z而非议案x投赞成票的投票人人数,有n(z![]() ix)=nⅡ。其中,i代表委员会中的任意投票人。
ix)=nⅡ。其中,i代表委员会中的任意投票人。
比较y和z两项备选议案,令n(y![]() iz)表示为议案y而非议案z投赞成票的投票人人数,有n(y
iz)表示为议案y而非议案z投赞成票的投票人人数,有n(y![]() iz)=nⅠ+nⅢ;令n(z
iz)=nⅠ+nⅢ;令n(z![]() iy)表示为议案z而非议案y投赞成票的投票人人数,有n(z
iy)表示为议案z而非议案y投赞成票的投票人人数,有n(z![]() iy)=nⅡ+nⅣ。其中,i代表委员会中的任意投票人。
iy)=nⅡ+nⅣ。其中,i代表委员会中的任意投票人。
在以上分析的基础上,我们来介绍简单多数规则定理及其证明过程。
定理7.3(简单多数规则定理):委员会能够依靠简单多数规则为任意三项备选议案x、y和z定义某一序关系![]() ,当且仅当所有投票人的偏好序都能够同时满足完备性、自返性、传递性等理性公理假设,并且符合极值限制公理假设的要求。
,当且仅当所有投票人的偏好序都能够同时满足完备性、自返性、传递性等理性公理假设,并且符合极值限制公理假设的要求。
1.定理的充分性证明
下面我们将尝试证明下述命题,当所有投票人的偏好序都能够同时满足完备性、自返性和传递性三个理性公理假设,并且符合极值限制公理假设的要求时,在简单多数规则的约束下,委员会可以为任意的三项备选议案x、y和z定义某一序关系![]() 。
。
证明:下面采用反证法来证明上述命题。假设当所有投票人的偏好序都能够同时满足完备性、自返性和传递性三个理性公理假设,并且符合极值限制公理假设的要求时,无法为任意三项备选议案x、y和z定义某一序关系![]() ,也就是说,委员会为任意三项备选议案的排序不能够同时满足完备性、自返性和传递性等理性公理假设的要求。
,也就是说,委员会为任意三项备选议案的排序不能够同时满足完备性、自返性和传递性等理性公理假设的要求。
如果所有投票人通过投票过程得出的结论是z 、y x和x z,那么,委员会关于x、y和z三项备选议案的排序不满足传递性假设。在简单多数规则的约束下,为了使z y成立,就要有nⅡ+nⅣ≥nⅠ+nⅢ;为了使y x成立,就要有nⅡ+nⅢ≥nⅠ+nⅣ;为了使x z成立,就要有nⅠ≥nⅡ。上述不等式只有在nⅡ=nⅠ且nⅣ=nⅢ时才能够同时成立,此时委员会对x、y、z三项备选议案的排序为x~y~z,能够满足传递性假设的要求。
上述推导过程得出的结论与前文无法为x、y、z三项备选议案定义某一序关系![]() 的假设相互矛盾。可见,当所有投票人的偏好序能够满足完备性、自返性和传递性三个理性公理假设,同时还符合极值限制公理假设的要求时,在简单多数规则的约束下,委员会能够为任意三项备选议案x、y、z定义某一序关系
的假设相互矛盾。可见,当所有投票人的偏好序能够满足完备性、自返性和传递性三个理性公理假设,同时还符合极值限制公理假设的要求时,在简单多数规则的约束下,委员会能够为任意三项备选议案x、y、z定义某一序关系![]() 。
。
2.定理的必要性证明
下面我们将尝试证明下述命题,当所有投票人的偏好序不能够同时满足完备性、自返性、传递性和极值限制公理假设的要求时,在简单多数规则的约束下,委员会将无法为任意三项备选议案x、y和z定义某一序关系![]() 。
。
假设委员会中所有投票人的偏好序都能够满足完备性、自返性和传递性三个理性公理假设的要求,却存在着违反极值限制公理假设的情况。假设可以找到某位投票人i,对于任意三项备选议案x、y和z,i的偏好序可以表示为x![]() i y
i y![]() iz,假设同时还能够找到某一更偏好于议案z而非议案x的投票人j,且j的偏好序可以表示为y jz jx或者z
iz,假设同时还能够找到某一更偏好于议案z而非议案x的投票人j,且j的偏好序可以表示为y jz jx或者z![]() jx jy。i和j两位投票人同时出现在委员会中,这违反了极值限制公理假设的要求。
jx jy。i和j两位投票人同时出现在委员会中,这违反了极值限制公理假设的要求。
假设委员会中只有i和j两位投票人,当投票人i的偏好序为x iy iz,而投票人j的偏好序为y jz x时,根据简单多数规则,委员会关于x、y、z三项备选议案的排序将会是x~y![]() z~x;当投票人i的偏好序为x jy jz,而投票人j的偏好序为zjx jy时,根据简单多数规则,委员会关于x、y、z三项备选议案的排序将会是x
z~x;当投票人i的偏好序为x jy jz,而投票人j的偏好序为zjx jy时,根据简单多数规则,委员会关于x、y、z三项备选议案的排序将会是x![]() y~z~x。可见,存在投票人的偏好序违反极值限制公理假设的要求时,委员会关于任意三项备选议案x、y、z的排序将不满足传递性,从而不能依靠简单多数规则为任意三项备选议案定义某一序关系
y~z~x。可见,存在投票人的偏好序违反极值限制公理假设的要求时,委员会关于任意三项备选议案x、y、z的排序将不满足传递性,从而不能依靠简单多数规则为任意三项备选议案定义某一序关系![]() 。
。
通过以上过程,我们粗略地证明了简单多数规则定理。
根据简单多数规则定理,所有投票人的偏好序都满足完备性、自返性、传递性和极值限制公理假设的要求,上述假设条件是简单多数规则约束下均衡投票结果存在的充分必要条件。即便能够找到某一条单一的议案维度,极值限制公理假设也允许投票人的偏好序存在违背单峰偏好假设的情况,可见,单峰偏好假设并不是简单多数规则约束下均衡投票结果存在的必要条件。
当所有投票人的偏好序不能够同时满足完备性、自返性、传递性和极值限制公理假设的要求时,在简单多数规则的约束下,委员会无法为任意三项备选议案定义某一序关系![]() ,这时,投票过程将再次面临陷入循环问题的可能性。关于委员会的投票过程中可能会出现的循环问题,我们将在第六篇介绍。
,这时,投票过程将再次面临陷入循环问题的可能性。关于委员会的投票过程中可能会出现的循环问题,我们将在第六篇介绍。
第四节 简单评价
直接民主制中的公共选择问题是较早引起学者们关注的一个研究领域,在按照直接民主制原则构造的理想世界中,只存在选民这样一类行为主体,他们提出备选议案并投出自己的选票。当然,由于经济中的个人人数和备选的议案数目都非常庞大,直接民主制这种看似简单的政治组织形式在现实生活中是难以实现的。在后面几章中我们将介绍更加具有现实意义的代议民主制。
此外,本章在介绍过程中遵循一些较早期经济学家的做法,假设所有选民都诚实地投出自己的选票,并且不会选择弃权行为。关于选民投票行为的进一步分析,我们将在第八章介绍。
本章着力探讨直接民主制条件下个人的行为选择,也涉及有关循环问题的一些内容。出现循环问题时,委员会的投票结果会在一些备选议案中间转来转去。当然,循环问题不仅仅出现在学者们在直接民主制条件下对公共选择问题的研究中,在后文介绍代议民主制中的公共选择问题时,我们还会遇到循环问题。另一方面,循环问题的存在还意味着公共选择经济理论与政治现实之间存在着巨大的差距,因为现实的政治过程并没有经常地陷入循环问题之中。关于公共选择经济学中的循环问题,我们将留在第六篇进行更加详细的介绍。
基本概念和术语
直接民主制 单峰偏好假设 普洛特“完美平衡”条件 中位数投票人循环问题 极值限制公理假设
思考题
1.请简单介绍单峰偏好假设与一维议案的中位数投票人定理。
2.请简单介绍多维议案的中位数投票人定理。
3.请简单介绍极值限制公理假设与简单多数规则定理。
4.请比较单峰偏好假设与极值限制公理假设。
【注释】
[1]本书把类似上述投票过程中出现的情况称为循环问题,关于循环问题的系统阐述将留在第六篇进行。如果按照肯尼思·约瑟夫·阿罗的表述,这里所说的循环问题应该被称为投票悖论。关于投票悖论这一经济学术语,本书沿用丹尼斯·C.缪勒的做法,用它来表示一种关于选民投票行为的质疑,即总是会有成千上万的选民选择参与投票过程,虽然他为此付出的成本往往要大于投票给他带来的收益。对于这一质疑,后文将有更为详细的介绍。
[2]传统的西方经济学要求个人偏好序满足完备性、自返性、传递性等理性公理假设,类似的假设条件也被公共选择经济学秉承下来。但是,这里介绍的极值限制公理假设是公共选择经济学讨论循环问题时引入的,在西方主流经济学中是没有的。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。

















