统计过程控制的常用工具

第二节　统计过程控制的常用工具

GB/T 19000—2000族标准中指出，“应用统计技术可帮助组织了解变异，从而有助于组织解决问题并提高有效性和效率。这些技术也有助于更好地利用可获得的数据进行决策。”

统计过程控制（Statistical Process Control），简称SPC，是企业提高质量管理水平的有效工具。它利用数理统计原理，通过对过程特性数据的收集和分析，达到“事前预防”的效果，从而有效控制生产过程、协同其他手段持续改进、提升品质。SPC技术的出现，使质量管理从被动的事后把关改变为过程中积极的事前预防，从而大大降低了企业的生产成本，同时也提高了企业的竞争能力。目前SPC已成为生产过程中控制稳定产出的主要工具之一，在生产型企业中应用非常广泛。

SPC是一系列工具的集合，包括发现质量缺陷、寻找质量波动的原因、监视过程的波动状况以及对异常波动及时报警的一系列方法。主要包括：检查表、分层法、排列图、因果图、散布图、直方图、波动图。

一、检查表

检查表（Data－Collection Form）又叫调查表、核对表、统计分析表，是用来收集资料和数据，对事实进行粗略整理和分析的统计表。常见的检查表有不合格检查表、缺陷位置检验表、质量分布检查表等。检查表的常见形式如表7－1所示。

表7－1　检查表的例

二、分层法

分层法（Stratification）又叫分类法、分组法。分层的目的在于把杂乱无章和错综复杂的资料或意见归类汇总，使之更清楚地反映客观现实。分层应使层内的数据差异尽可能小，而层与层之间的差异尽可能大，否则就起不到分层归类的作用。

分层的一般方法如下：

（1）按操作者分层。可按操作者个人分层，也可以按班组分层，还可以依据操作者的年龄、工级、性别分层。

（2）按设备分层。可按设备的不同类型、新旧程度、处于不同的生产线等进行分层。

（3）按原材料分层。可按产地、批号、制造厂、规范进行分层分析，有助于我们选择合适的供应商。

（4）按方法分层。可按不同的操作参数、操作方法、生产速度等分层。

（5）按时间分层。可按不同的班次、日期等分层。

（6）按环境分层。可按照明度、清洁度、湿度、温度等分层。

（7）其他。可按测量方法、使用条件等分层。

运用分层法时，必须考虑各种因素的综合影响效果。例如，某产品加工时经常出现缺陷。经抽查50个产品后发现，产生缺陷的原因和加工时操作者采用的方法及产品的型号有关。因此，采用表7－2所示的二因素综合分层法。由表7－2可知，当加工甲型产品时，应推广操作者2的方法；当加工乙型产品时，应推广操作者1的方法，因为这样做的缺陷率都为零。

表7－2　二因素分层表的例

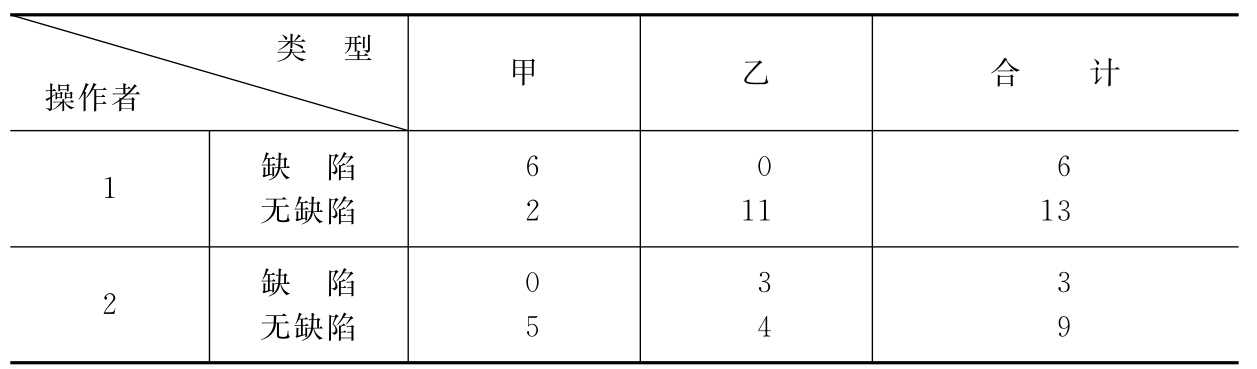
续　表

三、排列图

排列图又叫帕累托图（Pareto Diagram）或ABC分类法。它是分析和识别影响质量的主要因素，寻找质量改进机会，所采用的一种图示技术。排列图由两个纵坐标、一个横坐标、几个顺序排列的直方和一条累计百分率曲线所组成。

应用步骤如下：

（1）确定分析的对象。可以是某种产品（零件）的废品件数、吨数、损失金额、消耗工时及不合格项数等。

（2）确定问题分类的项目。可按废品项目、不合格品项目、零件项目、不同操作者等进行分类。

（3）确定收集数据的时间。

（4）收集数据。

（5）整理数据。列表汇总每个项目发生的频数，由大到小排列（“其他”项不论发生的频数大小，皆放在最后一项）。计算各项目累计发生的频数与累计百分率。

（6）画图。横坐标表示项目，按上表中的顺序由左到右排列；左边的纵坐标表示项目发生的频数，右边的纵坐标表示项目发生的累积百分率；直方的高度表示对应项目发生的频数；画累积百分率曲线。将排列图名称、分析对象总数、生产单位、绘图者、绘图时间等标在图上。

（7）根据排列图，选择严重影响质量的、累积百分率最大的或较大的一个或几个关键问题作为质量改进项目。

例如，某厂对铸铁件的废品吨数进行排列图分析。分类的项目是气孔、浇不足、夹砂、硬度低、裂纹与其他。数据整理略。根据数据整理表，画出排列图（图7-4）。从排列图可知，应首先选择气孔问题作为质量改进目标。

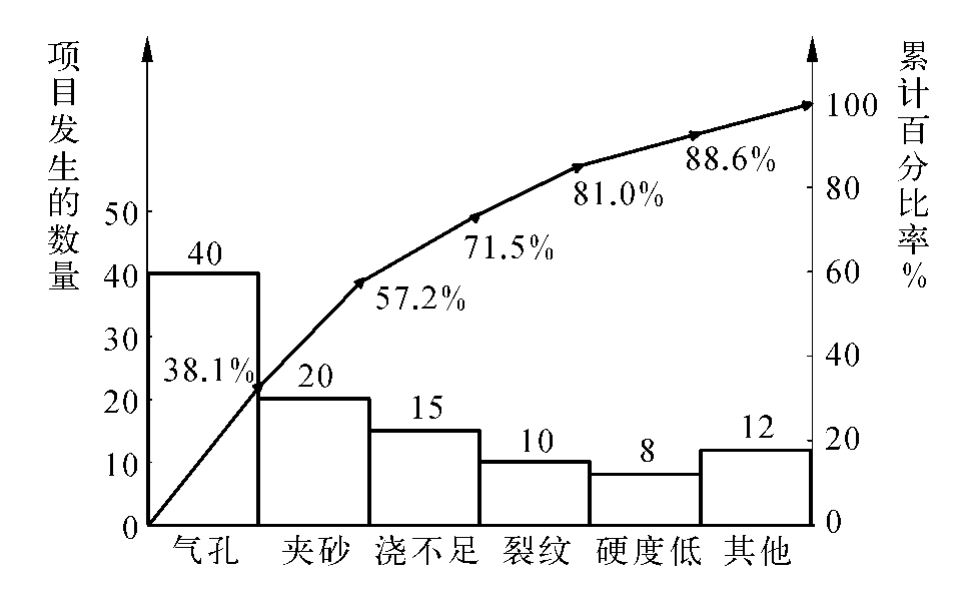
图7－4　排列图的例

四、因果图

因果图（Cause－effect diagram）又叫鱼刺图、石川图、特性要因图、树杈图，是表达和分析质量波动特性与其潜在原因的因果关系的一种图表。因果图由质量问题和影响因素两部分组成。图中主干箭头所指的为质量问题，主干上的大枝表示影响因素的大分类（如操作者、机器、材料、方法、环境等），中枝、小枝、细枝等表示因素的逐次展开。图7－5是因果图的一个例子。

五、散布图

散布图适用于判断两个变量之间是否存在相关关系。散布图由分布在直角坐标系中的一系列点子构成。

散布图的绘图步骤如下：

图7－5　控制器停工期因果图

（1）选定分析对象。可以是质量特性值与因素之间的关系、质量特性值与质量特性值之间的关系、因素与因素之间的关系。

（2）记录观测值与其名称、取样方法、取样日期、测定方法、测定仪器、观测值、环境条件等。

（3）在坐标纸上建立直角坐标系，把数据（x，y）分别标在坐标系上。

（4）当散布图上出现明显偏离其余数据的点时，应查明原因，以便决定是否删除或校正。

例9　发生炉煤气的质量取决于一氧化碳（CO）的含量，但测定较难，而测定二氧化碳（CO₂）较容易，故希望能得知CO₂和CO含量的关系。

解：过程如下：

（1）分析对象：质量特性值CO和CO₂含量的关系。

（2）收集生产中积累的30对数据（略）。

（3）建立直角坐标系，把数据（x，y）分别标在坐标系上，见图7－6。

图7－6　CO和CO₂含量的关系

由图7－6可见，CO（y）和CO₂（x）之间有显著的负相关关系。

（4）计算相关系数。列表计算（部分，见表7－3）。

表7－3　相关系数计算表

……

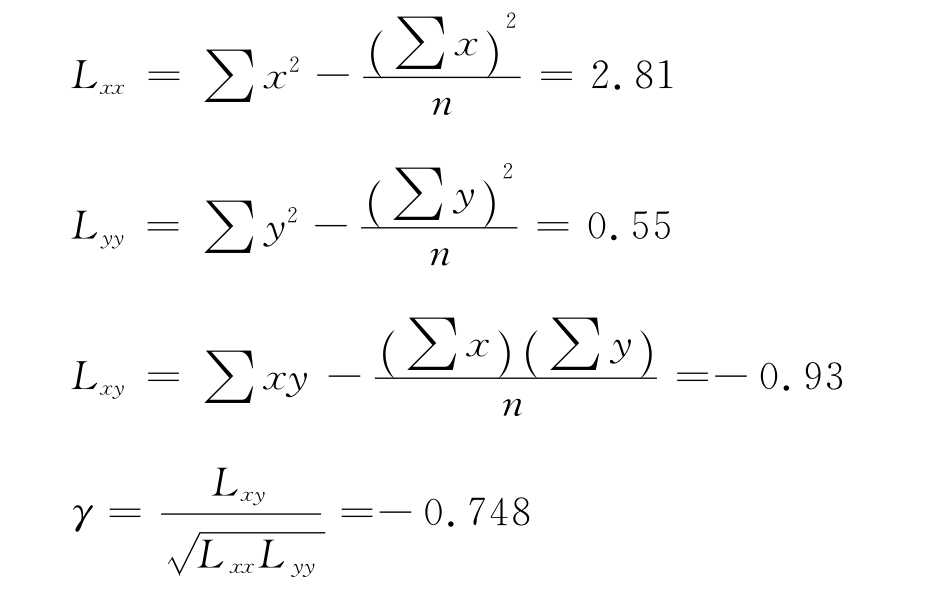
取α＝0．01，n－2＝28。查相关系数表得γ_α＝0．463，因∣－0．748∣＞0．463，故判定变量x与y在α＝0．01水平上存在较显著的负相关关系。

（5）在散布图上画回归直线。

在散布图上画出回归直线，见图7－7。

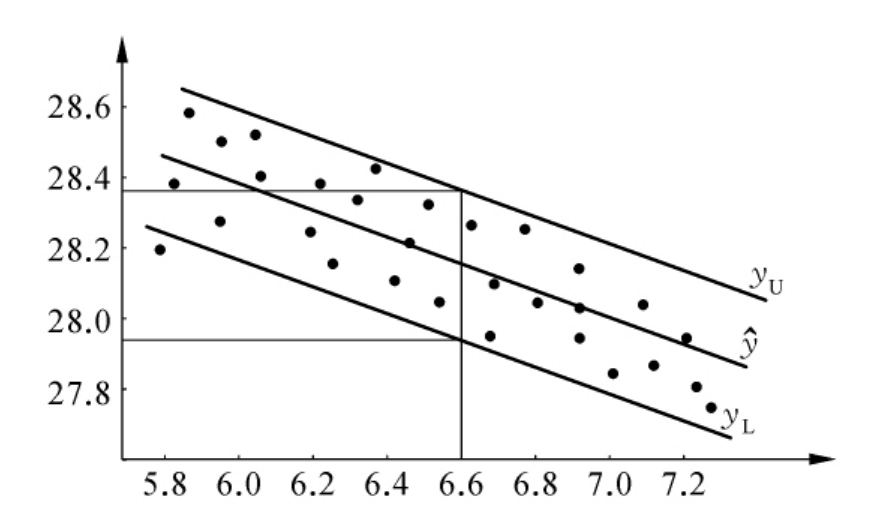
图7－7　回归直线

根据多年生产实践经验，认为该直线与实际情况拟合得较好。

计算回归直线的标准偏差s：

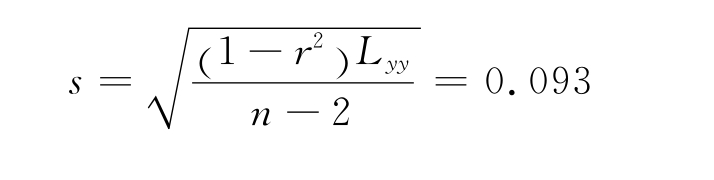
计算控制界限（选用2倍标准偏差）：

控制上限：y_U＝a＋2s＋bx＝30．526－0．33x

控制下限：y_L＝a－2s＋bx＝30．154－0．33x

在散布图上画出上、下控制界限见图7－7。

（6）预测。

当检测的煤气中CO₂含量x_o＝6．6%时，从图7－7中可以推测输出煤气中的CO含量y在27．97%～28．34%范围内。

六、直方图

直方图适用于分析观测值分布的状态，以便对总体的分布特征进行推断。直方图是由直角坐标系中若干顺序排列的长方形组成。各长方形的底边相等，为观测值区间，长方形的高为观测值落入相应区间的频数。

绘图步骤一般如下：

（1）收集n个观测值（n≥50）。

（2）找出观测值中的最大值x_L，最小值x_S。

（3）确定观测值大约的分组数k。

（4）确定各组组距h。

h＝（x_L－x_S）/k

（5）确定各组组界。首先确定第一组下组界，然后依次加入组距h，即可得到各组组界。观测值不能落在组界上。

（6）作频数表。计算频数f。

例10　加工某种轴，直径要求为85±0．001。100根轴的直径测量值从略。测量值中最大值x_L＝85．005mm，最小值x_S＝84．993。取大约的分组数k＝7。因此，各组组距h＝（85．005－84．993）/7≈0．001 7≈0．002mm。

各组组界（mm）和频数统计见表7－4。

表7－4　各组组界和频数统计

直方图见图7－8。

图7－8　数据直方图

计算均值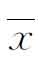，标准差s：

x₀＝84．9995　　∑fv＝－2　　　∑fv²＝208

在应用中，分析直方图的形状并与规范界限比较可以判断总体正常或异常，进而寻找异常的原因。常见的直方图有对称型分布、偏向型分布、双峰型分布、锯齿型分布、平顶型分布、孤岛型分布等，分析时要着眼于形状的整体。

七、波动图

波动图适用于观察和分析质量特性值随时间波动的状态，以便监视其变化。波动图为直角坐标系中一条波动曲线。横坐标表示抽取观测值的顺序号（或时间），纵坐标表示观测的质量特性值，波动曲线是根据不同时刻的观测值打点连线得到的。在图上可标出规范界限。波动图的重要应用是控制图，将在第八章作专门介绍。

本章小结

本章介绍生产过程中质量波动的统计规律性和统计质量控制的基本任务，以及几种常用的离散型随机变量和连续型随机变量。对统计过程控制的几种常用工具，如检查表、分层法、排列图、因果图、散布图、直方图、波动图等的概念和使用方法也作了简要介绍。