接近段控制器设计

由于接近段通常采用微波雷达测量视线参数，而且控制任务是减小视线距离，所以适宜用视线动力学方程描述系统的相对动力学方程，并以视线动力学方程为依据设计控制。

1.接近段过程解耦

在交会对接系统中，系统中存在的藕合因素体现在两点：姿态控制系统与轨道控制系统之间存在藕合；系统的相对动力学模型中，变量之间也存在藕合（C－W方程中x，z之间存在藕合；视线动力学方程中r，p，q之间存在藕合）。为了便于系统设计，需要对系统进行解藕设计。

在现有的解藕方法中，适于非线性系统的解藕方法主要有输入输出解藕方法、逆系统解藕方法和多变量频域设计方法。其中，输入输出解藕方法、逆系统解藕方法以状态空间理论为基础［110～111］，能够得到完全解藕的设计结果，但存在如下问题：对数学模型的精确度要求高，若系统中存在不确定性因素，这两种方法的鲁棒性较差，需要复杂的计算，不便于在自主交会对接系统中使用。多变量频域设计方法以古典控制理论中的频域设计理论为基础，通过对系统的传递函数进行对角化设计以实现近似解藕［112］。该方法在应用中的问题是：不便于将非线性系统的视线动力学方程转化为传递函数，且该方法的鲁棒特性有待提高。

在航天系统中，经常采用时标分离原理将复杂系统转化为若干个快慢有别的子系统，其基本思想是：若系统状态直接受控制作用影响，该状态“变化最快”；若系统状态受“变化最快”状态的控制，则该状态为“快变化”状态；若系统状态受“快变化”状态控制，则该状态为“慢变化”状态，关于时标分离原理及其用应用参见文献［113～117］。

在交会对接控制系统中，时标分离原理可以应用于如下方面：对于姿轨控动力系统，姿态控制系统为快变化系统，而轨道控制系统为慢变化系统；对于独立的轨道控制系统，由控制力产生的加速度量是“变化最快”的量，其次是由加速度变化引起的速度量为“快变化”状态，位移量则为“慢变化量”；对于姿态控制系统来说，由力矩产生的角加速度量是“变化最快”的量，姿态角变化率或角速度是“快变化”量，而姿态角是“慢变化”量。

在交会对接系统中，还需要对系统的被控变量进行分类。根据变量对控制任务的影响程度，将被控变量分为主控变量和辅助控制变量。其中，主控变量对控制任务的完成起决定性作用，辅助控制变量对控制任务的完成起辅助性作用。

基于上述时标分离和变量分类原则，本书提出了一种过程解藕策略。该策略通过适当安排对接进展过程的时序，减弱被控变量间的藕合，使复杂的控制系统分离成若干个独立的子系统，每个子系统的设计可以得到简化。

采用过程解藕的控制方法，将控制步骤分为如下步骤：

①进行姿态对准，使航天器姿态与所需轨控力方向重合，消除姿态控制系统对轨道控制系统的影响。

④在姿态稳定和视线角速度稳定情况下，控制r→rsafe，完成控制任务，其中rsafe为系统接近段终点的视线距离。

上述过程解藕流程，如图11所示。上述过程解藕流程并不是固定不变的，在实际使用中可以根据具体情况进行调整，比如，若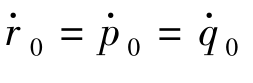=0，可以直接从第①步跳到第④步。

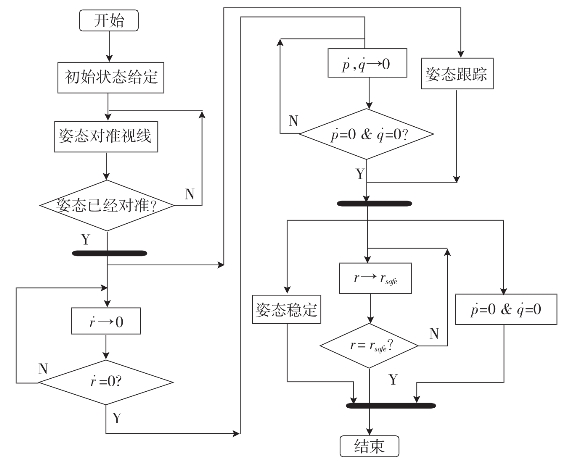
图11　接近段过程解耦流程

2.节能型MSMC设计

选定表1中No.6的数据设计主控变量r的滑模面，则

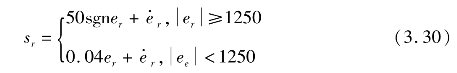
其中er=rsafe－r。该滑模面表明系统的接近速度为50m／s，滑模面连接点为1250m。根据表1可直接估计，接近过程所需的时间为298s，速度增量为100m／s。

由于交会对接控制系统中，发动机以开关方式工作，设计r，p，q方向的控制律为

其中Ar=1m／s2，Ap=Aq=0.25m／s2为轨控加速度幅值。

3.滑动模态吸引区域和存在区域

将系统的视线动力学方程改写为

其中

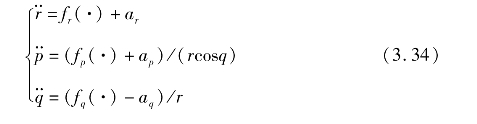
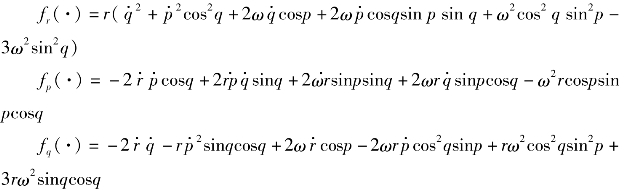
根据式（3.30）得

由于er=rsafe－r，所以

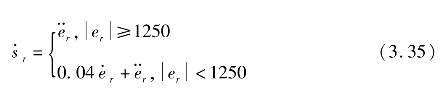
将式（3.34）中¨r代入式（3.36）得

当sr＞0时，将ar=sgn sr=1代入式（3.37）得

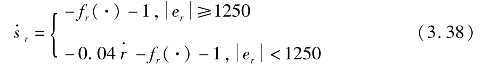
由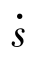sr ＜0得

当sr＜0时，将ar=sgn sr=－1代入式（3.37）得

由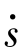sr ＞0得

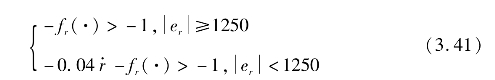
综合式（3.39）和（3.41）得，sr所表征的滑动模态的吸引区域为

式（3.42）所表示的吸引区域与滑模面sr的交集为滑动模态的存在区域。

根据式（3.31）得，

将式（3.34）中p¨代入式（3.43）得

在接近过程中，r＞0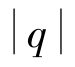，q ＜90°，所以r cos q不会变号。若sp＞0，由于ap= 0．25sgn sp=0.25，所以

若sp＜0，由于ap=0．25sgn sp=－0.25，所以

所以，sp代表的滑动模态的吸引区域为

同理，式（3.47）所代表的吸引区域与sp的交集为滑动模态的存在区域。

对于sq，其滑动模态的吸引区域和存在区域的确定方法与sp的确定方法类似，结果为

同理，式（3.48）所代表的吸引区域与sq的交集为滑动模态的存在区域。

4.系统稳定性

在滑动模态的吸引区域和存在区域证明系统的稳定性。

在滑动模态存在区域内，稳定性证明如下：

根据式（3.30）知，

对于sp，利用等效控制证明系统的稳定性。由于在滑动模态上，sp=0， =0，所以，在r cos q≠0时，根据式（3.31）、（3.34）得，sp所代表的滑动模态的等效控制为

将（3.50）代入式（3.34）得，p¨=0，所以系统在sp所代表的滑动模态上稳定。同理可知，系统在sq代表的滑动模态上稳定。

综上所述，系统在滑动模态的吸引区域和存在区域内均稳定。