递推数列通项求解方法

递推数列通项求解方法

江翠云

数列问题的题目在高考中常以压轴题的地位出现，尤以递推数列类型频率最高。而由递推关系确定数列通项往往是解决问题的关键。解决这类问题，必须具备科学的思维策略和清晰的思维层次，抓住特殊与一般、变形与化归、归纳推理与逻辑证明的关系，才能使问题得到顺利解决。

求数列通项公式的方法多样:定义法、公式法［如利用公式a_n= S_n－S_n－1(n≥2)］、累加法［a_n+1－a_n= f(n)，f(n)可求前n项和，n∈N^*］、累积法［a_n+1= g(n)a_n，g(n)可求前n项积］、迭代法、构造法(待定系数法)、分类讨论、数学归纳法。下面通过典型例子重点介绍其中两类方法。

一、构造相关的等差(比)数列求通项

通过对已知的递推关系式的合理变形(两边同除以一个非零因式，开方、平方、取倒数、取对数，引入参数待定等)后得到一个与所求通项的数列相关的等差(比)数列的通项，而稍作变形(运算)便可获得所求数列的通项。

1．直接变形构造

例1　(1)在数列{a_n}中，a₁=2，a_{n+ 1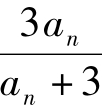}=，求数列{a_n}的通项a_n．

分析:∵a_n+1=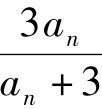

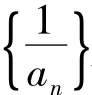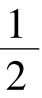∴是首项为，公差为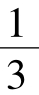的等差数列。

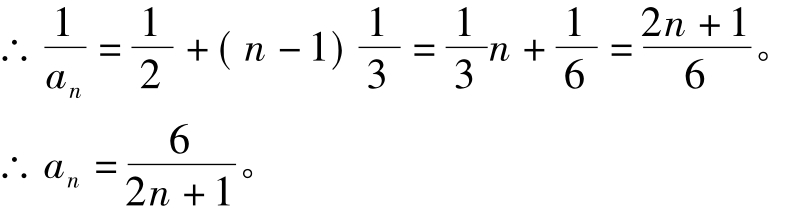
(2)数列{a_n}中，a₁=3且a_{n+ 1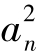}=，求a_n。

解析:由a_{n+ 1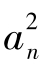}=且a=3知a＞0且a≠1，∴两边同时取常用对数得

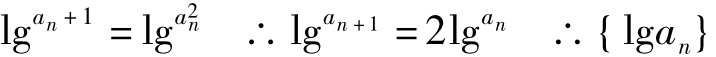是以lg³为首项，2为公比的等比数列。

评析:本题也可用迭代法求解，由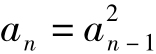得

(3)对数列{a_n}，规定{Δa_n}为数列{a_n}的一阶差分数列，其中，Δa_n= a_{n+ 1}－a_n(n∈N*)，对正整数k，规定{Δ^k a}为数列{a}的k阶差分数列，其中，Δ^k a=Δ^k－1 a－Δ^k－1 a _nnnn+1n=Δ(Δ^k－1 a)，若a= 1，且满足Δ² a－Δa+ a=－2ⁿ(n∈N*)，求a．_{n1nn+ 1nn}

解析:由已知得Δ² a=Δa－Δa代入Δ² a－Δa+ a=－2ⁿ_nn+1nnn+1n

得Δa－a=2ⁿ即(a)－a= 2ⁿ∴a－2a=2ⁿ_nnn+1nn+1n

两边同除以2^{n+ 1}得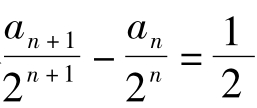

则数列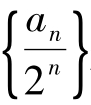是首项、公差均为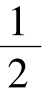的等差数列

评析:得a_n+1=2a_n+ 2ⁿ，由a₁=1，逐步计算得

a₂= 4= 2×2¹，a₃=12=3×2²，a₄= 3₂=4×2³

猜想a_n= n·2^n－1，再用数列归纳法易证其正确性．透过数字现象看本质，发现规律，归纳——猜想——证明．

2．引入参数待定构造

例:(1)已知数列{a_n}中，a₁=1，a_n=2a_n－1+1(n≥2，n∈N*)，求a_n．

设a_n+λ=2(a_n－1+λ)即a_n=2a_n－1+λ与(1)式对比得λ=1

∴a_n+ 1= 2(a_n－1+ 1)∴{a_n+ 1}是首项为2，公比为2的等比数列

∴a_n+ 1=2ⁿ，即a_n=2ⁿ－1

(2)已知数列{a_n}中，a₁=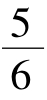，a_{n+ 1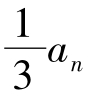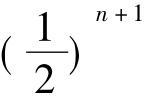}=+(n∈N*)，求a_n．

可设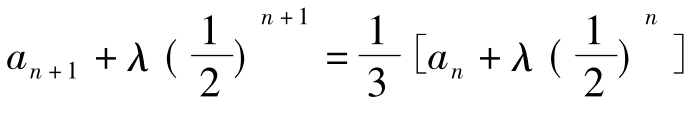(λ为常数)

即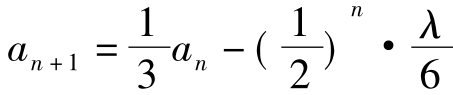与(1)式对比得λ=－3

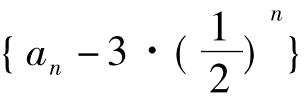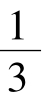∴数列是公比为，首项为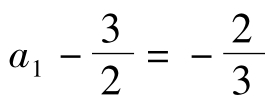的等比数列

故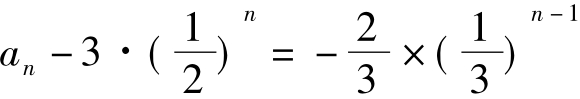从而得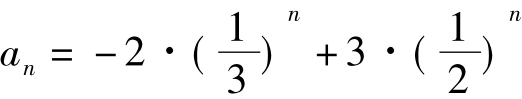

评析:上述例题中，递推关系a_n+1－2a_n=2ⁿ与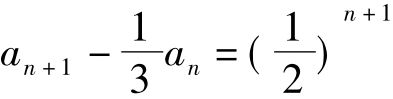有惊人的相似之处，而由其求通项的方法却截然不同，值得对比与思考。

(3)数列{a_n}中，a₁= 1，a₂= 4，a_{n+ 1}= 3a_n－2a_n－1(n≥2，n∈N*)，求a_n。

解:设a_{n+ 1}－λa_n=μ(a_n－λa_n－1)(λ、μ为常数)

∴a_{n+ 1}=(λ+μ)a_n－λ·μa_n－1与已知a_{n+ 1}=3a_n－2a_n－1对比得: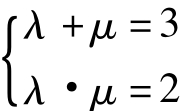

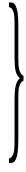消去a_n+1得a_n= 3·2^n－1－2由(1)得a_n+1－a_n=(a₂－a₁)·2^n－1=3·2^n－1

由(2)得a_{n+ 1}－2a_n=(a₂－2a₁)=2

(4)数列{a_n}中，a₁=4，a_n= 2a_n－1+ 3ⁿ－4ⁿ，求a_n。

解:设a_n=2a_n－1+3ⁿ－4ⁿ……(1)可变形为

a_n+ A·3ⁿ+ B·4ⁿ= 2(a_n－1+ A·3^n－1+ B·4^n－1)(A、B为待定系数)……(2)

即a_n= 2a_n－1－A·3^n－1－2B·4^n－1=2a_n－1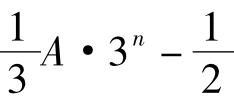－ B·4ⁿ与(1)式对比得: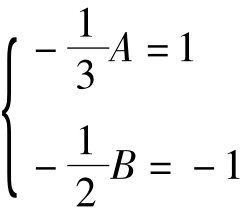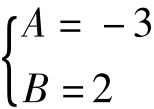，∴代入(2)得(1)式可变形为

a_n－3×3ⁿ+2×4ⁿ=2(a_n－1－3×3^n－1+ 2×4^n－1)

∴{a_n－3×3ⁿ+ 2×4ⁿ}是以a₁－3²+2×4=3为首项，2为公比的等比数列

∴a_n－3ⁿ⁺¹+2×4ⁿ=3×2^n－1即a_n=3ⁿ⁺¹+3×2^n－1－2×4ⁿ

评析:对已知的递推关系两边采取哪一种变形方能得到一个与要求通项的数列相关的等差(比)数列，关键要抓住递推关系式的结构特征［齐次、非齐次、分式，连续两项(三项)的线性关系］及变形的目标［得到一个相关的等差(比)数列］，一般不能用直接变形构造的方式(取倒数、取对数、两边同除以一个非零因式等)时，不妨引入一个或两个参数构造相关数列再通过与已知的递推关系式系数的对比，就可获得参数取值，求出新构造的数列的通项后再易得所求数列的通项。

二、分类讨论求通项

我们所讨论的数列都是有规律的数列，然而一些数列其规律不适合用前面所所讨论的方法去找寻，但其所有奇数项、偶数项分别成等差(比)数列或各具特征，这时必须通过分别对奇数项、偶数项的探讨方可得其通项。

例:(1)数列{a_n}满足a₁=1，a_n·a_n+1=4ⁿ，求a_n。

解析:∵a_n·a_n+1=4ⁿ∴a_n+1·a_n+2=4ⁿ⁺¹相比得: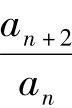= 4(n∈N*)

又由a₁=1得a₂= 4，∴数列{a_n}的所有奇数项及其所有偶数项分别成等比数列，公比均为4，首项分别为a₁= 1，a₂=4。

n为偶数时，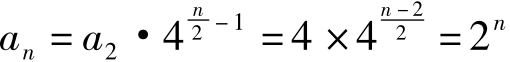

n为奇数时，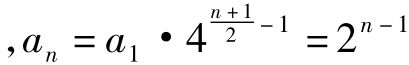

评析:由递推关系a·a= 4ⁿ的推理得数列隔项成等比，但整个数列{a}并不成_{nn+ 1n}等比，不能一概而论时，必须合理分类加以讨论。

(2)数列{a_n}中，a₁=1且a_{n+ 1}+ a_n= 3×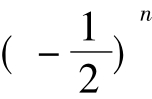(n∈N*)

解:由a₁= 1及a_{n+ 1}+ a_n=3×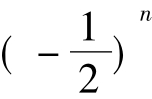……(1)得a₂=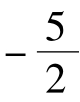

a_n+ a_n－1= 3×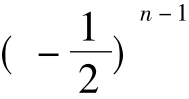，(n≥2)……(2)

由(1)－(2)得:a_n+1－a_n－1=3×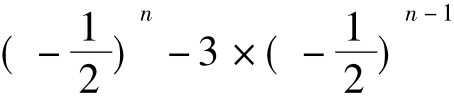

即a_n+1－a_n－1=9×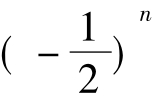(n≥2)

∴数列{a_n}的所有奇数项和偶数项分别用累加法可得其通项。

即得a_2k+1=4－3×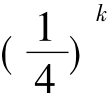= 4－3×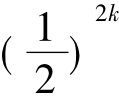(k=0时也合)

∴n为奇数时a_n=4－3×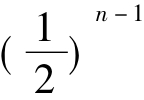

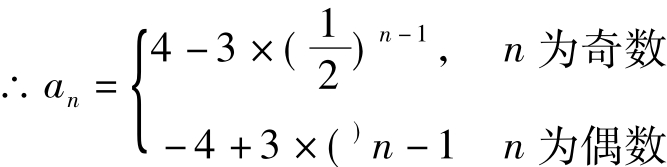
也可统一为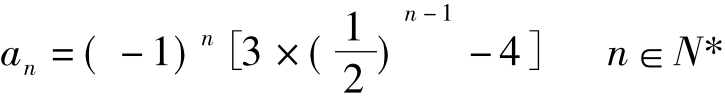

评析:通项能写成统一的形式时，必须统一，结论统一较繁时，可考虑用分段函数形式表达。